Neurčitý integrál
Maple používá k integraci specialní algoritmy (a to tehdy, pokud základní metody (per partes, rozklad na parc. zlomky, ...)) selhávají.
Procedura Int integrál nevyhodnocuje, pouze přepisuje.
| > | Int(x/(x^3+1), x):%=value(%); |
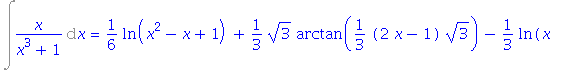
![]()
Vyhodnocení dosáhneme příkazem value.
Kontrola správnosti výpočtu derivováním:
| > | diff(rhs(%), x); |
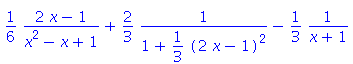
| > | normal(%,'expanded'); |
![]()
Více informací o průběhu výpočtu získáme nastavením
| > | infolevel[int]:=2: |
| > | Int(x/(x^5+1),x): %=value(%); |
int/indef1: first-stage indefinite integration
int/ratpoly: rational function integration
int/ratpoly: rational function integration
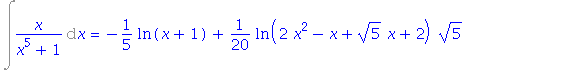
![]()
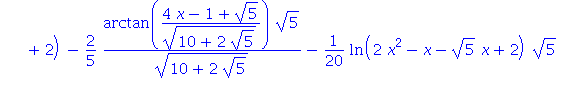
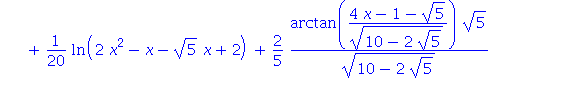
| > | infolevel[int]:=0: |
Pozn. Maple při výpočtech automaticky volí nulovou integrační konstantu.
Přiklad 1.
| > | Int(2*x*(x^2+1)^24, x); |
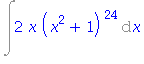
Tento integrál jste jistě schopni vyřesit bez pomoci Maplu, přímým výpočtem ale dostáváme
| > | value(%); |
![]()
![]()
![]()
![]()
a ani úpravy výsledku nepomáhají
| > | v1:=factor(%); |
![]()
![]()
![]()
![]()
Problém je zde právě ve volbě integrační konstanty
| > | v2:=factor(%+1/25); |
![(Typesetting:-mprintslash)([v2 := 1/25*(x^2+1)^25], [1/25*(x^2+1)^25])](images/int1_18.gif)
| > | plot([v1, v2], x=-.5..0.5, y=0..1); |
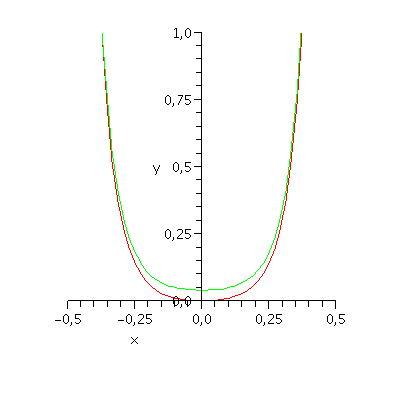
Cvičení. Vytvořte pomoci Maplu tabulku neurčitých integrálů.
Novější verze Maplu (od verze 8) umožňují kromě výsledku zobrazit i postup výpočtu (pomocí příkazu Hint a Rule
z balíku Student[Calculus1] . Těchto příkazů pak využívá nová procedura VypocetIntegralu.
| > | read VypocetIntegralu: |
| > | VypocetIntegralu(exp(x)*sin(x), czech); |
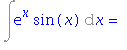
![]()
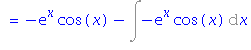
![]()
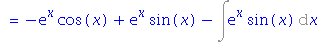
![]()
![]()
![]()
![]()
| > |