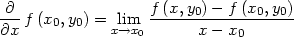
[Další] [Předchozí] [Předchozí – na konec] [Na konec] [Výše]
V této kapitole je z výpočetního hlediska velmi efektivní použití počítačového systému k přímým výpočtům parciálních derivací, zejména při kontrole výsledků náročnějších výpočtů. Pomocí PC-grafů můžeme také znázorňovat geometrický význam parciálních a směrových derivací.
Pomocí Maplu lze Definici 3.1
zapsat následujícím způsobem:
> Diff(f(x[0],y[0]),x)=
> Limit((f(x,y[0])-f(x[0],y[0]))/(x-x[0]),
x=x[0]);
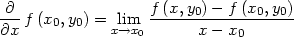
> Diff(f(x[0],y[0]),y)=
> Limit((f(x[0],y)-f(x[0],y[0]))/(y-y[0]),
y=y[0]);
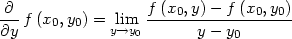
Označíme–li x
− x0
= h a y
− y0
= k, můžeme použít analogického zápisu:
> Diff(f(x[0],y[0]),x)=
> Limit((f(x[0]+h,y[0])-f(x[0],y[0]))/h,
h=0);
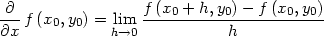
> Diff(f(x[0],y[0]),y)=
> Limit((f(x[0],y[0]+k)-f(x[0],y[0]))/k,
k=0);
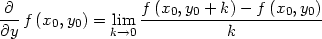
Příklad 12.1. Určete parciální derivace
funkce f(x,y) =
x4y2
−xy + 7
v obecném bodě [x,y
]
i) podle definice.
> f:=(x,y)->x^4*y^2-x*y+7;
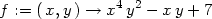
> Limit((f(x+h,y)-f(x,y))/h, h=0):"=value(");
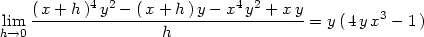
> Limit((f(x,y+k)-f(x,y))/k, k=0):"=value(");
Tedy
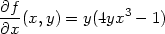
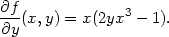
ii) Využitím příkazu diff. Maple umožňuje i přímý
výpočet parciálních derivací. Ten využíváme tehdy, pokud je
parciální derivování dostatečně procvičeno a rutinními výpočty
se nechceme dále zdržovat, případně ke kontrole správnosti výpočtu.
K symbolickému derivování používáme příkazu diff pro výrazy a funkčního operátoru D pro funkce1:
> Diff(f(x,y),x):"=value(");
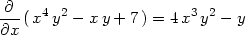
> factor(");
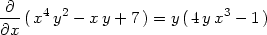
> Diff(f(x,y),y):"=factor(value("));
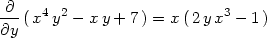
> D[1](f);
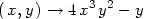
> factor(D[1](f)(x,y));
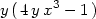
> factor(D[2](f)(x,y));
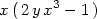
Grafických možností Maplu využijeme nyní i k znázornění geometrického významu parciálních derivací. PC-grafem znázorníme geometrický význam parciální derivace funkce f(x,y) = x + y2 −x3y podle x v bodě [1,2].
Generujme postupně PC-graf funkce f (p1),
rovinu  : y
= 2 (p2, za využití příkazu drawplane z knihovny
mvcalp), křivku, která je
průsečnicí roviny
: y
= 2 (p2, za využití příkazu drawplane z knihovny
mvcalp), křivku, která je
průsečnicí roviny  s grafem funkce f (p3)
a konečně tečnu k této křivce
v bodě [1,2] (p4),
ležící v rovině
s grafem funkce f (p3)
a konečně tečnu k této křivce
v bodě [1,2] (p4),
ležící v rovině  . Parciální
derivace funkce f
podle x udává směrnici
této tečny (smerx). Jednotlivé
PC-grafy nevykreslujeme na obrazovku, v závěru je pomocí
příkazu display3d složíme do výsledného
PC-grafu (obr. 12.1
):
. Parciální
derivace funkce f
podle x udává směrnici
této tečny (smerx). Jednotlivé
PC-grafy nevykreslujeme na obrazovku, v závěru je pomocí
příkazu display3d složíme do výsledného
PC-grafu (obr. 12.1
):
> f:=(x,y)->x+y^2-x^3*y;
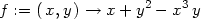
> bod:=[1,2];
![bod := [1,2 ]](diferencialni-pocet1208x.png)
> p1:=plot3d(f(x,y),x=-2..2,y=-3..3,axes=framed):
> with(mvcalp):
> with(plots):
> p2:=drawplane(y=bod[2],x=-2..2, z=-10..20,
> axes=framed):
> p3:=plot3d([x,bod[2],f(x,bod[2])],x=-2..2,y=-3..3,
> axes=framed, thickness=3, color=black):
> smerx:=limit((f(bod[1]+h,bod[2])-f(bod[1],bod[2]))/h,
> h=0);
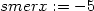
> p4:=spacecurve(evalm([bod[1],bod[2],
> f(bod[1],bod[2])]+t*[1,0,smerx]),
> t=-3..1, color=black, thickness=3):
> display3d({p1,p2,p3,p4}, labels=[x,y,z]);
Obdobně generujme i PC-graf znázorňující
parciální derivaci podle y. Zkoumaná funkce je zde uvedena
z jiného úhlu pohledu (obr. 12.2):
> g2:=drawplane(x=bod[1],y=-3..3,z=-10..20):
> g3:=plot3d([bod[1],y,f(bod[1],y)], x=-2..2, y=-3..3,
> thickness=3, color=black):
> smery:=limit((f(bod[1],bod[2]+h)-f(bod[1],bod[2]))/h,
> h=0);
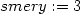
> g4:=spacecurve(evalm([bod[1],bod[2],f(bod[1],bod[2])]
> +t*[0,1,smery]), t=-4..1, color=black, thickness=3):
> display3d({p1,g2,g3,g4}, labels=[x,y,z],
> orientation=[129,-131]);
Uvedené postupy jsou univerzální a umožňují generovat tento PC-graf pro libovolnou funkci, která má v zadaném bodě parciální derivace pouze změnou zadání funkce a souřadnic bodu, ve kterém parciální derivace počítáme. Samostatné generování těchto PC-grafů studenty v počítačové laboratoři je vhodným cvičením na pochopení geometrického významu parciálních derivací.
Skutečnost, že z existence parciálních derivací funkce f(x,y) v bodě [x0,y0] neplyne spojitost v tomto bodě, ilustruje následující příklad:
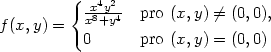
má v bodě [0,0] obě
parciální derivace (rovny nule):
> limit((f(x,0)-f(0,0))/(x-0), x=0);
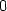
> limit((f(0,y)-f(0,0))/(y-0), x=0);
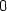
a není zde spojitá, neboť blížíme–li se
k bodu [0,0] po
parabolách y = kx2,
dostáváme:
> Limit(f(x, k*x^2), x=0)=limit(f(x, k*x^2), x=0);
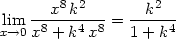
To však znamená, že lim(x,y)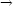 (0,0)f(x,y)
neexistuje a tedy funkce f
není v bodě [0,0]
spojitá (obr. 12.3
).
(0,0)f(x,y)
neexistuje a tedy funkce f
není v bodě [0,0]
spojitá (obr. 12.3
).
> plot3d(f, -1..1, -1..1, style=patchcontour,
> axes=boxed, grid=[100,100], orientation=[-45,35],
> contours=7, labels=[x,y,’z’]);
K výpočtu derivací vyšších řádů se používá stejného příkazu jako pro derivaci prvního řádu, navíc pouze zadáme, kolikrát podle které proměnné derivujeme. Efektivnost výpočtu ilustrujme na následujícím příkladě:
Příklad 12.3. Ukažte, že pro funkci
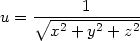
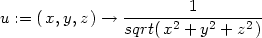
> st := time():
> diff(u(x,y,z),x$2)+diff(u(x,y,z),y$2)+
> diff(u(x,y,z),z$2);
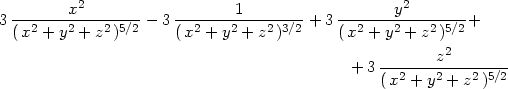
|
Tím je zkoumaná rovnost ověřena. Dobu výpočtu v
sekundách určíme příkazem:
> time() - st;
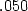
Následující příklad ukazuje, že bez předpokladu spojitosti smíšených parciálních derivací fxy, fyx v bodě [x0,y0] rovnost fxy(x0, y0) = fyx(x0, y0) obecně neplatí.
Příklad 12.4. Nechť je funkce f dána předpisem
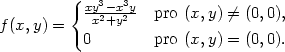
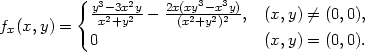
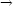 0
0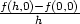 . Obdobně
. Obdobně
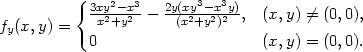
| fxy(0,0) | =
limh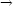 0 0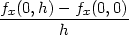 = limh = limh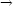 0 0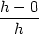 = 1, = 1, |
||
| fyx(0,0) | =
limh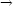 0 0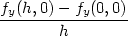 = limh = limh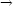 0 0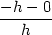 = −1. = −1. |
> D[1](f)(x,y);
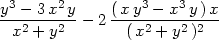
> D[2](f)(x,y);
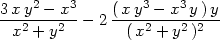
> fx0:=limit((f(h,0)-f(0,0))/h, h=0);
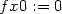
> fy0:=limit((f(0,h)-f(0,0))/h, h=0);
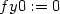
> limit((D[1](f)(0,h)-fx0)/h, h=0);
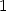
> limit((D[2](f)(h,0)-fy0)/h, h=0);
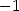
Počítačem generujme PC-graf funkce, kterou si
jinak umíme jen velmi obtížně představit. Tento PC-graf je zajímavý
i tím, že z něj není vidět, že smíšené parciální derivace
nejsou záměnné (obr. 12.4
):
> plot3d(f, -3..3, -3..3, style=patch, axes=boxed,
> labels=[x,y,’z’]);
Na rozdíl od parciálních derivací nemáme
v Maplu k dispozici přímý příkaz k výpočtu směrových
derivací. K výpočtu tedy používáme přímo Definice 3.3
. V Maplu zápis vypadá
takto:
> Limit((f(x[0]+t*u[1], y[0]+t*u[2])-f(x[0],y[0]))/t,
> t=0);
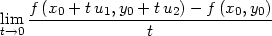
Příklad 12.5. Určete směrovou derivaci funkce
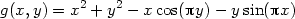
 ,1∕
,1∕ ).
).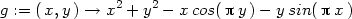
a nyní aplikujme definici:
> Dg(-1,2):=limit((g(-1+t*2/sqrt(5),
> 2+t*1/sqrt(5))-g(-1,2))/t, t=0);
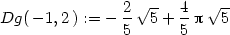
Ke znázornění geometrického významu směrových derivací použijeme podobného postupu jako u derivací parciálních. Generování tohoto PC-grafu je opět vhodným cvičením na pochopení geometrického významu a definice směrových derivací.
PC-grafem znázorníme směrovou derivaci funkce f(x,y) = x2 + y2 ve směru vektoru u = (1,1) v bodě [1,1].
Tvorbu rozdělme do několika samostatných částí,
postupně generujme PC-graf funkce f (s1),
rovinu y = x (s2,
znázorňuje směr vektoru u,
v tomto případě ji zadáváme parametricky), křivku, která je
průsečnicí roviny s grafem funkce (s3, tedy funkci jedné proměnné  (t),
jejíž derivaci hledáme) a konečně tečnu k
(t),
jejíž derivaci hledáme) a konečně tečnu k  (t)
v bodě [1,1]
(s4). Výsledný PC-graf je znázorněn
na obrázku 12.5
.
(t)
v bodě [1,1]
(s4). Výsledný PC-graf je znázorněn
na obrázku 12.5
.
> f:=(x,y)->x^2+y^2;
> bod:=[1,1];
![bod := [1,1 ]](diferencialni-pocet1246x.png)
> u:=[1,1];
![u := [1,1 ]](diferencialni-pocet1247x.png)
> s1:=plot3d(f(x,y), x=-3..3, y=-3..3):
> s2:=plot3d([bod[1]+u[1]*t, bod[2]+u[2]*t,z], t=-4..2,
> z=-5..18, grid=[5,5]):
> with(plots):
> s3:=spacecurve([bod[1]+u[1]*t, bod[2]+u[2]*t,
> f(bod[1]+u[1]*t, bod[2]+u[2]*t)], t=-4..2,
> thickness=3, color=black):
> smer:=limit((f(bod[1]+t*u[1],
> bod[2]+t*u[2])-f(bod[1], bod[2]))/t, t=0);
> s4:=spacecurve(evalm([bod[1],bod[2], f(bod[1],
> bod[2])]+t*[u[1],u[2],smer]), t=-2..2, thickness=3):
> display3d({s1,s2,s3,s4}, scaling=constrained,
> orientation=[-28,-170], labels=[x,y,z], axes=framed);
Změnou zadání funkce, bodu (bod) a vektoru u (u) můžeme generovat další PC-grafy.
V příkladu 12.2 jsme ukázali, že z existence parciálních derivací funkce f v bodě [x0,y0] neplyne spojitost funkce v tomto bodě. Nyní na stejné funkci ukážeme, že ani existence směrové derivace v bodě [x0,y0] ve směru libovolného vektoru u není postačující pro spojitost.
Příklad 12.6. Ukažte, že funkce f definovaná předpisem
![{-x4y2 f(x,y) = x8+y4 pro (x,y) ⁄= [0,0], 0 pro (x,y) = [0,0]](diferencialni-pocet1249x.png)

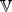 2 a
přesto není v tomto bodě spojitá. (
2 a
přesto není v tomto bodě spojitá. (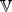 2 je
označení pro zaměření 2-rozměrného euklidovského
prostoru.)
2 je
označení pro zaměření 2-rozměrného euklidovského
prostoru.)
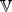 2
libovolný vektor, pak podle definice směrové derivace platí
2
libovolný vektor, pak podle definice směrové derivace platí
![1- -t4u41-⋅t2u22-- fu(0,0) = ltim→0 t[f(0+ tu1,0 + tu2) − f(0,0)] = ltim→0 t(t8u81 + t4u42) = 4 = lim -tu81u2-4-= 0. t→0 t4u1 + u2](diferencialni-pocet1250x.png)
|
> Limit((f(0+t*u[1], 0+t*u[2])-f(0,0))/t, t=0)=
> limit((f(0+t*u[1], 0+t*u[2])-f(0,0))/t, t=0);
Přitom v příkladu 12.2 jsem ukázali, že funkce f není v bodě [0,0] spojitá, viz také příklad 3.5 a obr. 12.3.
Výpočty parciálních derivací složené funkce dvou proměnných jsou úkolem poměrně početně náročným, v učitelském studiu dnes probíráme pouze výpočet parciální derivace složené funkce prvního řádu. Ukážeme zde možnost, jak tyto výpočty značně zjednodušit za pomoci počítače.
Pomocí Maplu lze vzorce pro parciální derivace 1.
řádu složené funkce dvou proměnných v obecném bodě
[u,v]
(Věta 5.1
) zapsat takto:
> dFdx:=Diff(f(u,v),u)*Diff(u(x,y),x)+
> Diff(f(u,v),v)*Diff(v(x,y),x);
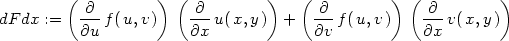
> dFdy:=Diff(f(u,v),u)*Diff(u(x,y),y)+
> Diff(f(u,v),v)*Diff(v(x,y),y);
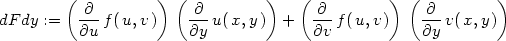
Úkolem pro studenty do počítačové laboratoře je
využití těchto vzorců v procedurách pro výpočet parciálních
derivací složených funkcí:
> dzd1:=proc(z,uu,vv,u,v,x,y)
> diff(z,u)*diff(uu,x)+diff(z,v)*diff(vv,x);
> end:
> dzd2:=proc(z,uu,vv,u,v,x,y)
> diff(z,u)*diff(uu,y)+diff(z,v)*diff(vv,y);
> end:
Procedury dzd1 a dzd2 určují parciální derivaci 1.
řádu složené funkce dvou proměnných. Parametry procedury jsou:
z je funkce z =
f(u,v),
uu je funkce u(x,y),
vv je funkce v(x,y) a
u, v, x a y jsou proměnné, ve kterých jsou
funkce zapsány (můžeme použít libovolné označení proměnných, viz
příklad 12.8
). Procedury můžeme použít i obecně na
funkce z(u,v),
u(x,y) a
v(x,y),
přičemž dzd1 počítá parciální derivaci
podle první proměnné (zde podle x) a dzd2 podle 2.
proměnné (y):
> dzd1(z(u,v), u(x,y), v(x,y), u,v,x,y);
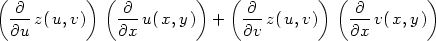
> dzd2(z(u,v), u(x,y), v(x,y), u,v,x,y);

Příklad 12.7. Je dána funkce z
= eu sinv,
kde u = xy a
v = x
+ y. Určete zx
a zy.
Použitím procedur dzd1 a
dzd2 dostáváme:
> zx:=dzd1(exp(u)*sin(v), x*y, x+y, u,v,x,y );
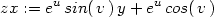
> zy:=dzd2(exp(u)*sin(v), x*y, x+y, u,v,x,y );
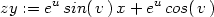
Dosazením za u
a v dostáváme:
> zx:=subs(u=x*y, v=x+y, zx);
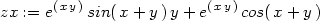
> zy:=subs(u=x*y, v=x+y, zy);
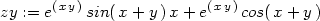
Poznámka 12.1. Pro řešení
příkladu 12.7
můžeme použít i přímého
výpočtu:
> u:=(x,y)->x*y;v:=(x.y)->x+y;
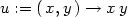
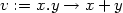
> vyraz:=exp(u(x,y))*sin(v(x,y));
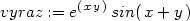
> zx:=diff(vyraz,x);
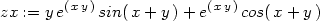
> zy:=diff(vyraz,y);
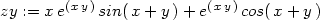
V tomto případě jsou však vzorce pro výpočet parciálních derivací složené funkce „skryty“ a tento postup je vhodný pouze pro kontrolu správnosti výpočtu.
Příklad 12.8. Transformujte rovnici
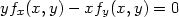
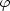 = arctan
= arctan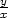 , r =
, r = 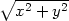 .
.
(označení z=z(r,phi) bylo
použito pro zjednodušení Mapleovského výstupu)
> zx:=dzd1(z, sqrt(x^2+y^2), arctan(y/x), r,phi,x,y);
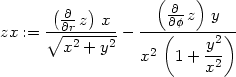
> zy:=dzd2(z, sqrt(x^2+y^2), arctan(y/x), r,phi,x,y);
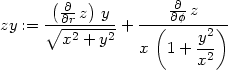
Což po úpravě dává rovnici:
> simplify(y*zx-x*zy=0);
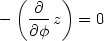
Poznámka 12.2. Řešení příkladu 12.8 opět za použití
přímého výpočtu:
> vyraz:=z(sqrt(x^2+y^2),arctan(y/x));
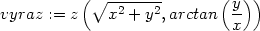
> zx:=diff(vyraz,x);
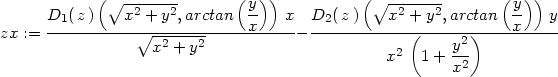
> zy:=diff(vyraz,y);
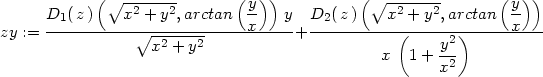
Označíme-li
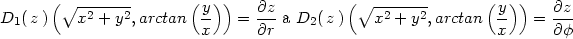
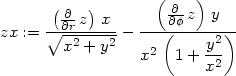
> zy:=subs({op(1,op(1,zy))=
> Diff(z,r),op(1,op(2,zy))=Diff(z,phi)},
zy);
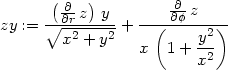
> simplify(y*zx-x*zy=0);
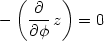
Podobným způsobem je možno naprogramovat i
procedury pro výpočet parciálních derivací druhého řádu:
> dzdd1:=proc(z,uu,vv,u,v,x,y)
> diff(z,u,u)*diff(uu,x)^2+2*diff(z,u,v)*diff(vv,x)*
> diff(uu,x)+diff(z,v,v)*diff(vv,x)^2+diff(z,u)*
> diff(uu,x,x)+diff(z,v)*diff(vv,x,x);
> end:
> dzdd2:=proc(z,uu,vv,u,v,x,y)
> diff(z,u,u)*diff(uu,y)^2+2*diff(z,u,v)*diff(vv,y)*
> diff(uu,y)+diff(z,v,v)*diff(vv,y)^2+diff(z,u)*
> diff(uu,y,y)+diff(z,v)*diff(vv,y,y);
> end:
> dzdd12:=proc(z,uu,vv,u,v,x,y)
> diff(z,u,u)*diff(uu,x)*diff(uu,y)+diff(z,u,v)*
> diff(vv,y)*diff(uu,x)+diff(z,u,v)*diff(vv,x)*
> diff(uu,y)+diff(z,v,v)*diff(vv,x)*diff(vv,y)+
> diff(z,u)*diff(uu,x,y)+diff(z,v)*diff(vv,x,y);
> end:
Zde dzdd1 je procedura pro výpočet druhé parciální derivace podle 1. proměnné, dzdd2 pro výpočet druhé parciální derivace podle druhé proměnné a dzdd12 pro výpočet smíšené parciální derivace, přičemž význam parametrů procedur je stejný jako u procedur pro výpočet prvních derivací.
Nyní si pomocí těchto procedur připomeňme vzorce
pro parciální derivace složené funkce 2. řádu v obecném
bodě [u,v]
(Věta 5.2
):
> alias(z=z(u,v));
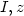
> dzdd1(z, u(x,y), v(x,y), u,v,x,y);
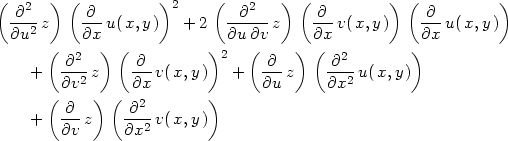
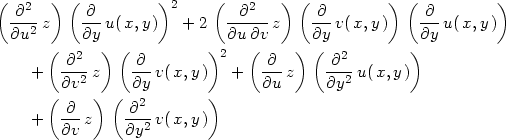
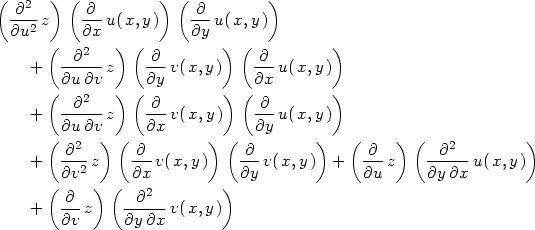
Příklad 12.9. Transformujte do nových nezávisle proměnných u = x + ay, v = x − ay rovnici
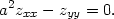
Využitím procedur dzdd1 a dzdd2 dostáváme:
> alias(z=z(u,v));
> zxx:=dzdd1(z, x+a*y, x-a*y, u,v,x,y);
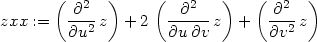
> zyy:=dzdd2(z, x+a*y, x-a*y, u,v,x,y);
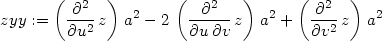
> simplify(a^2*zxx-zyy=0);
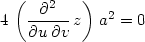
Příklad 12.10. Transformujte rovnici
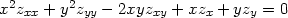
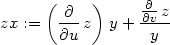
> zy:=dzd2(z, x*y,x/y,u,v,x,y);
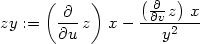
> zxx:=dzdd1(z, x*y,x/y,u,v,x,y);
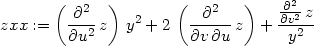
> zyy:=dzdd2(z, x*y,x/y,u,v,x,y);
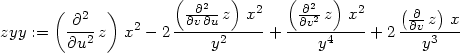
> zxy:=dzdd12(z, x*y,x/y,u,v,x,y);
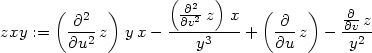
> tr:=expand(simplify(x^2*zxx+y^2*zyy-
> 2*x*y*zxy+x*zx+y*zy=0));
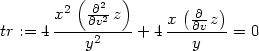
Dalšími úpravami dostáváme:
> tr:=factor(student[powsubs](x/y=v,tr));
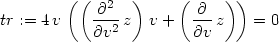
> tr/(4*v);
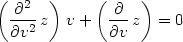
Příklad 12.11. Transformujte rovnici
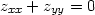
 ,
y = r
sin
,
y = r
sin za předpokladu, že funkce z má spojité parciální derivace
2. řádu.
za předpokladu, že funkce z má spojité parciální derivace
2. řádu.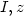
> zr:=dzd1(z, r*cos(phi), r*sin(phi), x,y,r,phi);
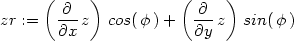
> zrr:=dzdd1(z, r*cos(phi), r*sin(phi), x,y,r,phi);
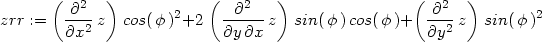
> zff:=dzdd2(z, r*cos(phi), r*sin(phi), x,y,r,phi);
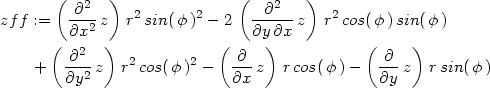

 , dostáváme:
, dostáváme: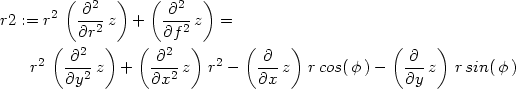
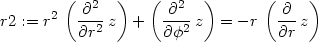
> lhs(r2)-rhs(r2)=0;
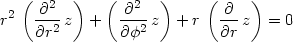
1Výraz a funkce ve smyslu základních datových struktur Maplu.
[Další] [Předchozí] [Předchozí – na konec] [Na začátek] [Výše]