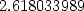Kapitola 14
Extrémy funkce
v Maplu
Tato část je pro počítačem podporovanou výuku
velmi vhodná. S využitím grafických i výpočetních možností
Maplu hledáme nejdříve lokální extrémy funkce dvou proměnných.
Volbou příkladů ukazujeme i na nebezpečí bezmyšlenkovitého použití
počítače k výpočtům, tj. zaměřujeme se na příklady, při
jejichž řešení pomocí Maplu dostáváme neúplné nebo nepřesné
výsledky. Často se opakující postupy poté automatizujeme pomocí
Mapleovského programovacího jazyka v procedurách. Obdobně
postupujeme i při hledání absolutních extrémů funkce dvou
proměnných.
14.1 Lokální extrémy
Pomocí grafických a výpočetních možností Maplu
budeme nyní ilustrovat problematiku lokálních extrémů funkce dvou
proměnných.
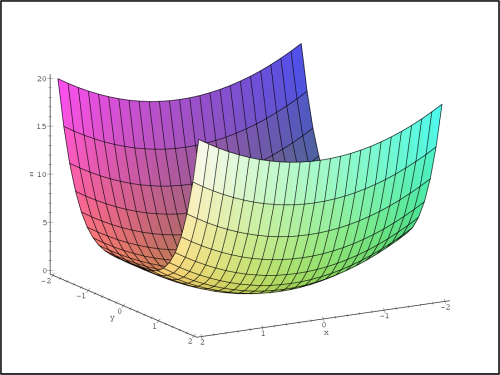
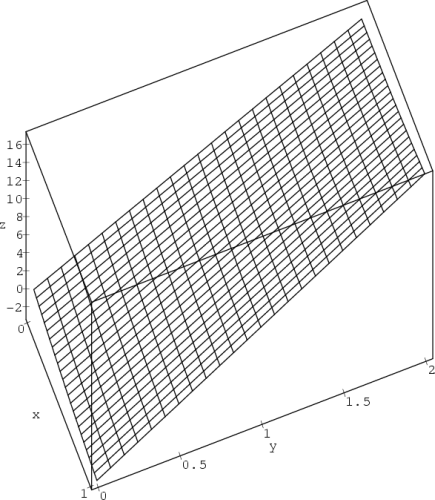
Příklad 14.1. Uvažujme funkci
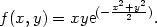 > f := (x,y) -> x*y*exp(-(x^2+y^2)/2);
> f := (x,y) -> x*y*exp(-(x^2+y^2)/2);
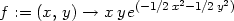
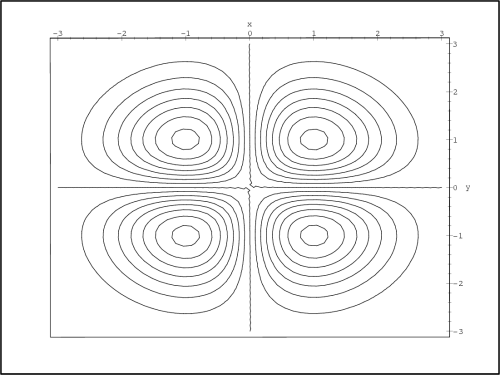
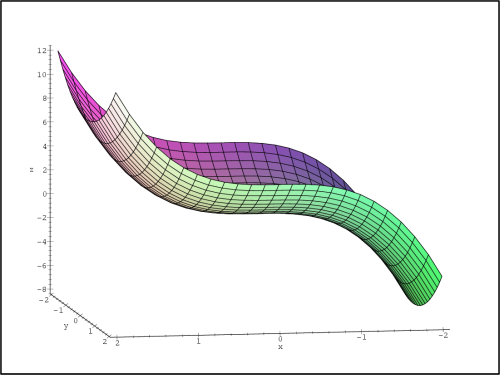
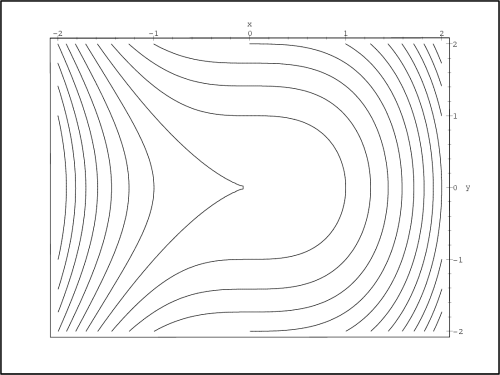
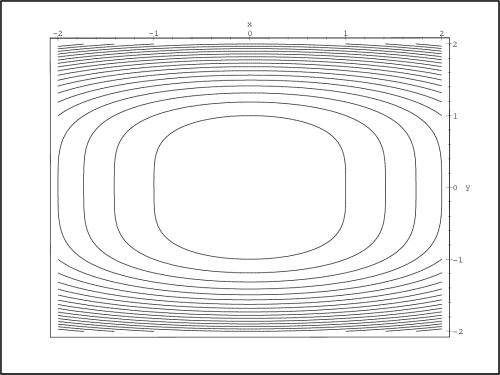
Generujme PC-graf funkce f (obr. 14.1
) a PC-graf, znázorňující vrstevnice
funkce f (obr. 14.2):
> plot3d(f(x,y),x=-3..3,y=-3..3,style =patch,
> orientation=[70,65], axes=FRAMED, grid=[40,30],
> labels=[x,y,z]);
> with(plots):
> contourplot(f(x,y),x=-3..3,y=-3..3, grid=[50,50],
> axes=boxed);
Z uvedených PC-grafů usuzujeme na lokální
extrémy v každém ze čtyř kvadrantů, a to na lokální maxima
v prvním a třetím kvadrantu a na lokální minima ve druhém a
čtvrtém kvadrantu. Tuto úvahu ověřme nyní výpočtem.
Stacionární body najdeme řešením soustavy rovnic
(viz Definice 6.2
)
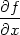 |
= 0 |
|
|
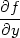 |
=
0. |
|
|
> cp:=solve({diff(f(x,y),x)=0,
> diff(f(x,y),y)=0}, {x,y});
Tedy, podle předchozí úvahy patrně v bodech
[1,1] a
[−1,−1]
nastává lokální maximum, v bodech [−1,1],
[1,−1]
lokální minimum a bod [0,0] je
sedlovým bodem. Tuto domněnku podpořme nejdříve generováním
PC-grafů funkce f
v blízkém okolí stacionárních bodů:
> plot3d(f(x,y),x=-0.1..0.1,y=-0.1..0.1,
> orientation = [70,65], style=patchcontour);
> plot3d(f(x,y),x=0.9..1.1,y=0.9..1.1,
> orientation = [70,65], style=patchcontour);
> plot3d(f(x,y),x=0.9..1.1,y=-1.1..-0.9,
> orientation = [70,65], style=patchcontour);
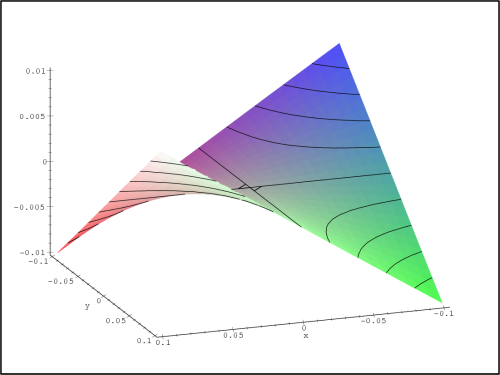
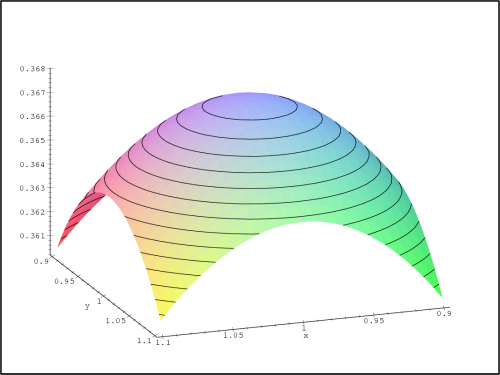
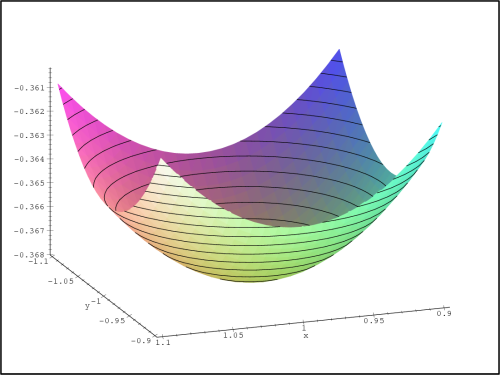
Na obrázku 14.3
je okolí bodu [0,0],
jedná se tedy o sedlový bod, obr. 14.4 znázorňuje okolí
bodu [1,1]
(lokální maximum) a obr. 14.5
znázorňuje okolí
bodu [1,−1]
(lokální minimum). Tyto úvahy podpořme opět výpočtem. Platí:
> fxx := factor(diff(f(x,y),x,x));
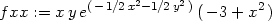
> fxy := factor(diff(f(x,y),x,y));
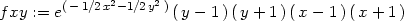
> fyy := factor(diff(f(x,y),y,y));
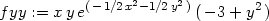
> Delta:=factor(fxx*fyy-fxy^2);
> eval(subs(x=0,y=0,Delta));
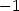
V souladu s dobře známou postačující
podmínkou existence a charakteru extrému ve stacionárním bodě
(Věta 6.2
) v bodě [0,0]
extrém nenastává, jde o tzv. sedlový bod (obr. 14.3). V bodě
[1,1]
nastává ostré lokální maximum (obr. 14.4), neboť:
> subs(x=1,y=1,[Delta,fxx]);
![[ ] 4 (e(−1))2,− 2e(−1)](diferencialni-pocet1471x.png)
Obdobně prokážeme, že v bodě [−1,1] a
[1,−1]
nastávají ostrá lokální minima a v bodě [−1,−1]
ostré lokální maximum:
> subs(x=-1,y=1,[Delta,fxx]);
![[ ] 4 (e(−1))2,2e(−1)](diferencialni-pocet1472x.png)
> subs(x=-1,y=-1,[Delta,fxx]);
> subs(x=1,y=-1,[Delta,fxx]);
![[ (−1) 2 (−1)] 4 (e ) ,− 2e](diferencialni-pocet1473x.png)
![[ ] 4 (e(−1))2,2e(−1)](diferencialni-pocet1474x.png)
Závěrem určeme funkční hodnoty v bodech
extrémů:
> zip(f,[1,-1,-1,1],[1,1,-1,-1]);
![(−1) (−1 ) (−1) (−1) [e ,− e ,e ,− e ]](diferencialni-pocet1475x.png)
V bodech [1,1] a
[−1,−1] je
tedy lokální maximum f(1,1) =
f(−1,−1) =
1∕e a v bodech
[1,−1] a
[−1,1]
lokální minimum f(1,−1) =
f(−1,1) =
−1∕e.
Předchozí příklad lze charakterizovat jako
standardní. Následující příklady však poukazují na problémy, které
při určování lokálních extrémů funkcí dvou proměnných pomocí Maplu
mohou vzniknout.
Příklad 14.2. Určete lokální extrémy funkce
f(x,y) =
x4 −3x2y
+3y−y3.
> f:= (x,y) -> x^4 - 3*x^2*y + 3*y - y^3;
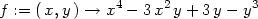
> fx := D[1](f);fy := D[2](f);
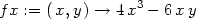
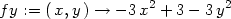
Parciální derivace položme rovny nule a pomocí
Maplu řešme získanou soustavu rovnic:
> cp := solve ({fx(x,y)=0, fy(x,y)=0}, {x,y});
První dvě řešení jsme schopni snadno interpretovat, u druhých
dvou je situace obtížnější. Převeďme proto řešení na snadněji
interpretovatelný tvar:
> cp := map (allvalues, {cp});
Nyní je vidět, že uvedená soustava rovnic má 6 řešení, dvě
z řešení jsou však komplexní čísla. Protože v celé práci
pracujeme v reálném oboru, komplexní kořeny odfiltrujeme pomocí
procedury
takereal (procedura je uložena
v knihovně
mvcalp):
> with(mvcalp):
> cp := takereal (cp);
Získali jsme tedy čtyři stacionární body
[0,1],
[0,−1],
[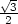 ,
, ]
] a
[−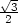 ,
, ]
].
Dále rozhodneme již standardním způsobem, zda má
funkce f v získaných
stacionárních bodech extrémy.
Spočtěme druhé parciální derivace funkce f:
> fxx := D[1](fx);
> fyy := D[2](fy);
> fxy := D[2](fx);
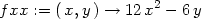
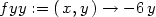
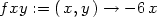
a určeme hodnotu Δ(x,y) =
fxxfyy
− [fxy]2 ve
stacionárních bodech:
> Delta:=fxx(x,y)*fyy(x,y)-fxy(x,y)^2;
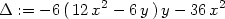
> for i from 1 to nops(cp) do
> cp[i],simplify(subs(cp[i], [Delta, fxx(x,y)]));
> od;
![{ } x = 1-√3,y = 1- ,[− 45,6 ] 2 2](diferencialni-pocet1490x.png)
![{ } x = − 1-√3,y = 1- ,[− 45,6 ] 2 2](diferencialni-pocet1491x.png)
![{x = 0,y = 1},[36,− 6]](diferencialni-pocet1492x.png)
![{x = 0,y = − 1 },[36,6]](diferencialni-pocet1493x.png)
Podle získaných hodnot má funkce f lokální minimum v bodě [0,−1] a
lokální maximum v bodě [0,1],
zbývající body jsou sedlové.
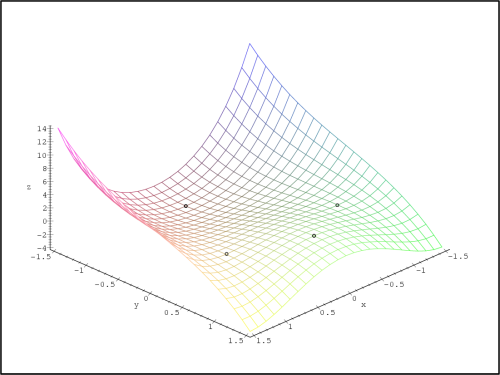
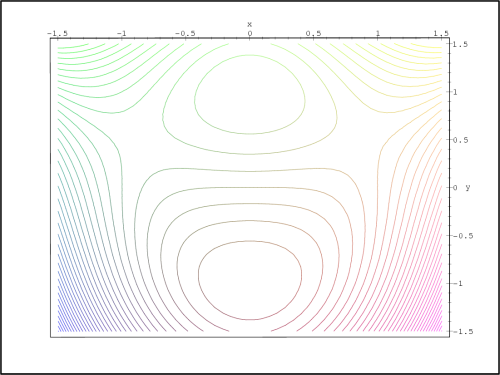
Generujme nyní PC-graf funkce f s vyznačenými stacionárními body
(obr. 14.6)
a vrstevnice f
(obr. 14.7
).
V práci používaná verze Maple V R3
neumožňuje grafické zvýraznění vybraného bodu v PC-grafu.
Zvýraznění bodu o souřadnicích [x,y,f(x,y)]
dosáhneme přidáním bodů [x,y,f(x,y) +
0,01] a [x,y,f(x,y)
− 0,01] do
PC-grafu:
> plt1 := plot3d (f(x,y), x=-1.5..1.5, y=-1.5..1.5):
> pts := {seq (subs (op(i, cp), [x,y,f(x,y)]),
> i=1..nops(cp)),
> seq (subs (op(i, cp), [x,y,f(x,y)+0.01]),
> i=1..nops(cp)),
> seq (subs (op(i, cp), [x,y,f(x,y)-0.01]),
> i=1..nops(cp))}:
> display3d ({plt1,
> pointplot (pts, symbol=circle, color=black)},
> axes=framed, labels=[x,y,’z’]);
> contourplot(f(x,y), x=-1.5..1.5, y=-1.5..1.5,
> axes=boxed, grid=[50,50], contours=20);
Poznámka 14.1. K výpočtu Δ můžeme použít i příkazu hessian(f(x,y),[x,y]);, kterým spočteme
matici
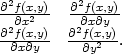
Odpovídající část výpočtu pak vypadá takto:
> with(linalg):
> h:=hessian(f(x,y), [x,y]);fxx:=D[1,1](f);
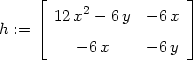
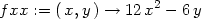
> Delta:=det(h);
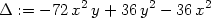
> for i from 1 to nops(cp) do
> cp[i],simplify(subs(cp[i], [Delta, fxx(x,y)]));
> od;
![{x = 0,y = 1},[36,− 6]](diferencialni-pocet1500x.png)
![{x = 0,y = − 1 },[36,6]](diferencialni-pocet1501x.png)
![{ 1 1 √ -} y = -,x = -- 3 ,[− 45,6 ] 2 2](diferencialni-pocet1502x.png)
![{ 1 1 √ -} y = -,x = − -- 3 ,[− 45,6 ] 2 2](diferencialni-pocet1503x.png)
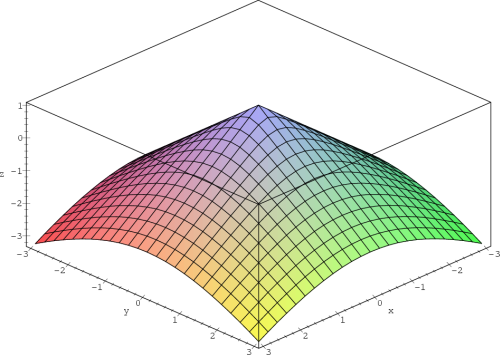
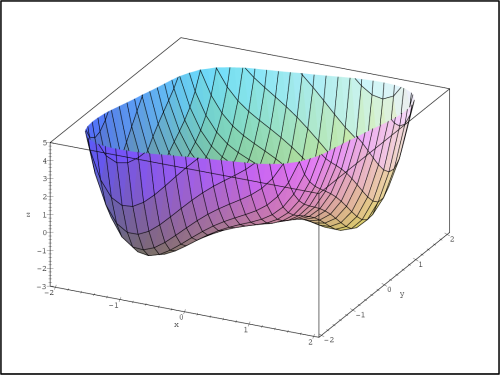
Příklad 14.3. Určete lokální extrémy funkce
z =
1 −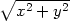 .
.
> z:=(x,y)->1-sqrt(x^2+y^2);
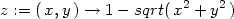
> plot3d(z(x,y),x=-3..3,y=-3..3,axes=boxed,
> labels=[x,y,’z’],style=patch);
Výsledek vidíme na obr. 14.8.
> cp:=solve({diff(z(x,y),x)=0,
> diff(z(x,y),y)=0}, {x,y});
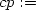
Daná funkce nemá stacionární body, nemůžeme tedy
použít dříve uvedený postup. Protože podle Poznámky 6.1
funkce f :
 2
2 
 může mít lokální extrém pouze ve svém
stacionárním bodě nebo v bodě, kde alespoň jedna
z parciálních derivací neexistuje, hledáme body, ve kterých
neexistují parciální derivace:
může mít lokální extrém pouze ve svém
stacionárním bodě nebo v bodě, kde alespoň jedna
z parciálních derivací neexistuje, hledáme body, ve kterých
neexistují parciální derivace:
> diff(z(x,y),x);diff(z(x,y),y);
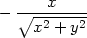
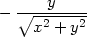
> D[1](z)(0,0);
Error, (in unknown) division by zero
V bodě [0,0]
neexistují parciální derivace prvního řádu, bod [0,0] je
bodem možného extrému. Přírůstek funkce z v tomto bodě z(x,y)
− z(0,0) =
−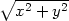 je záporný, tedy podle definice v bodě [0,0] má
funkce z maximum zmax = 1.
je záporný, tedy podle definice v bodě [0,0] má
funkce z maximum zmax = 1.
Příklad 14.4. Určete lokální extrémy funkce z =
xy ln(x2
+ y2).
> z:=(x,y)->x*y*ln(x^2+y^2);
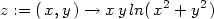
> plot3d(z(x,y),x=-1.1..1.1, y=-1.1..1.1, axes=framed,
> orientation=[-23,52], style=patch, labels=[x,y,’z’]);
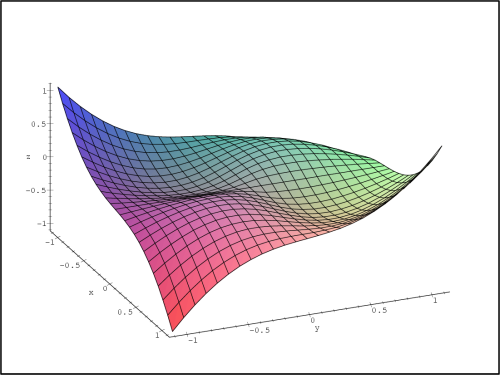
> contourplot(z(x,y), x=-1.1..1.1, y=-1.1..1.1,
> contours=25,numpoints=3000,color=black,axes=boxed);
> r1:=diff(z(x,y),x)=0;
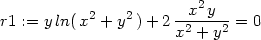
> r2:=diff(z(x,y),y)=0;
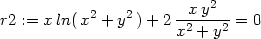
Řešme získanou soustavu:
> cp1:=solve({r1,r2}, {x,y});
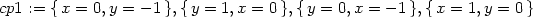
Při presentovaných výpočtech používaná verze
Maple V R3 v tomto případě není schopna symbolicky
nalézt všechna řešení. Vypočítané stacionární body jsou jen
[0, 1] a [
1] a [ 1,0].
Pomocí PC-grafů funkce z
(obr. 14.9)
a vrstevnic z
(obr. 14.10
) však usuzujeme, že v nalezených
stacionárních bodech extrém nenastává a dokonce, že uvažovaná
funkce má další čtyři stacionární body.
1,0].
Pomocí PC-grafů funkce z
(obr. 14.9)
a vrstevnic z
(obr. 14.10
) však usuzujeme, že v nalezených
stacionárních bodech extrém nenastává a dokonce, že uvažovaná
funkce má další čtyři stacionární body.
Stejný úkol nyní řešme s použitím
numerického řešení dané soustavy:
> cp2:=fsolve({diff(z(x,y),x)=0, diff(z(x,y),y)=0},
> {x,y}, {x=0..1, y=-1..0});
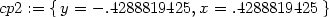
> cp3:=fsolve({diff(z(x,y),x)=0, diff(z(x,y),y)=0},
> {x,y}, {x=0..1, y=0..1});
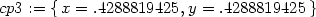
> cp4:=fsolve({diff(z(x,y),x)=0, diff(z(x,y),y)=0},
> {x,y}, {x=-1..0, y=-1..0});
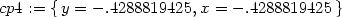
> cp5:=fsolve({diff(z(x,y),x)=0, diff(z(x,y),y)=0},
> {x,y}, {x=-1..0, y=0..1});
> cp:={cp1,cp2,cp3,cp4,cp5};
> fxx := D[1,1](z):fyy := D[2,2](z): fxy := D[1,2](z):
> Delta:=fxx(x,y)*fyy(x,y)-fxy(x,y)^2:
> for i from 1 to nops(cp) do
> cp[i],simplify(subs(cp[i], [Delta, fxx(x,y)]));
> od;
![{x = 0,y = − 1 },[− 4,0]](diferencialni-pocet1522x.png)
![{y = 1,x = 0 },[− 4,0 ]](diferencialni-pocet1523x.png)
![{y = 0,x = − 1 },[− 4,0]](diferencialni-pocet1524x.png)
![{x = 1,y = 0 },[− 4,0 ]](diferencialni-pocet1525x.png)
![{y = .4288819425,x = − .4288819425 },[4.,− 2.]](diferencialni-pocet1526x.png)
![{y = − .4288819425, x = .4288819425 },[4.,− 2.]](diferencialni-pocet1527x.png)
![{x = .4288819425, y = .4288819425 },[4.,2.]](diferencialni-pocet1528x.png)
![{y = − .4288819425, x = − .4288819425 },[4.,2.]](diferencialni-pocet1529x.png)
Numerický výpočet potvrzuje, že v bodech
[0, 1] a [
1] a [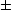 1,0]
extrém nenastává a navíc, že v bodech [
1,0]
extrém nenastává a navíc, že v bodech [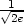 ,
,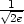 ] a [
] a [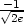 ,
,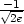 ] je lokální minimum a v bodech
[
] je lokální minimum a v bodech
[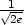 ,
,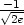 ] a [
] a [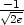 ,
,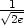 ] lokální maximum (viz příklad 6.3
-ii)).
] lokální maximum (viz příklad 6.3
-ii)).
Poznámka 14.2. Verze Maple V R4
již symbolicky řeší i soustavu pro získání všech stacionárních bodů
správně:
> z:=(x,y)->x*y*ln(x^2+y^2);
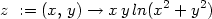
> cp1:=solve({diff(z(x,y),x)=0,
> diff(z(x,y),y)=0}, {x,y});
> cp1:=map(allvalues,{cp1});
Příklad 14.5. Najděte lokální extrémy
funkce z = (x2
+ y2)e−(x2+y2) .
Řešením systému
| zx
= |
(2x
− 2x(x2
+ y2))e−(x2+y2) = 0 |
|
|
| zy
= |
(2y
− 2y(x2
+ y2))e−(x2+y2) = 0 |
|
|
získáváme množinu stacionárních bodů, která se skládá z bodu
[0,0] a
bodů kružnice
x2
+ y2
= 1:
> z:=(x,y)->(x^2+y^2)*exp(-(x^2+y^2));
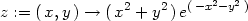
> cp:={solve({diff(z(x,y),x)=0,
> diff(z(x,y),y)=0}, {x,y})};
> fxx := D[1,1](z):fyy := D[2,2](z): fxy := D[1,2](z):
> Delta:=fxx(x,y)*fyy(x,y)-fxy(x,y)^2:
Protože:
> for i from 1 to nops(cp) do
> cp[i],simplify(subs(cp[i], [Delta, fxx(x,y)]));
> od;
![{y = 0,x = 1},[0,− 4e(−1)]](diferencialni-pocet1543x.png)
![{y = 0,x = − 1},[0,− 4 e(−1)]](diferencialni-pocet1544x.png)
![{ ∘ ------} x = x,y = 1 − x2 ,[0,− 4x2 e(−1)]](diferencialni-pocet1545x.png)
![{ ∘ -----2} 2 (−1) x = x,y = − 1− x ,[0,− 4x e ]](diferencialni-pocet1546x.png)
![{y = 0,x = 0 },[4,2 ]](diferencialni-pocet1547x.png)
![{x = 0,y = 1 },[0,0 ]](diferencialni-pocet1548x.png)
![{x = 0,y = − 1},[0,0 ]](diferencialni-pocet1549x.png)
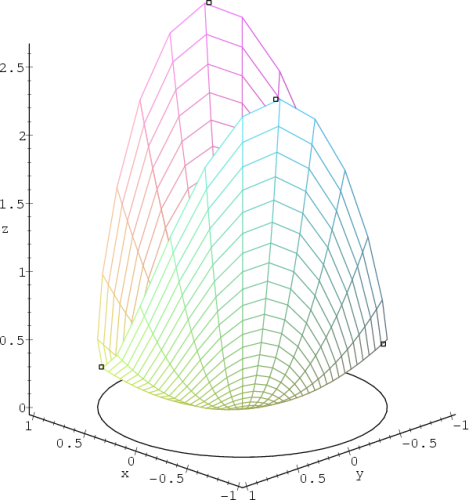
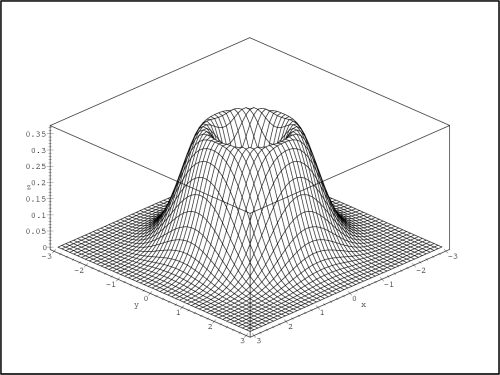
nastává v bodě [0,0]
lokální minimum (obr. 14.12
). O existenci extrému
v bodech kružnice nemůžeme tímto způsobem rozhodnout
(Δ je v bodech kružnice
x2 +
y2 = 1 rovno
nule).
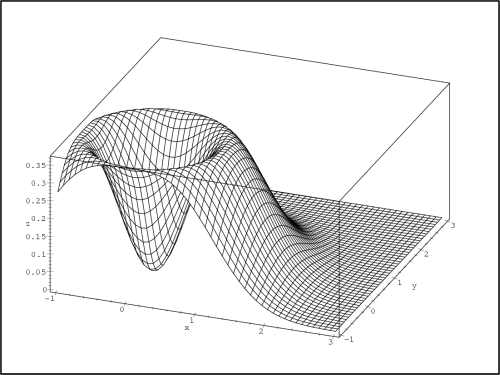
Pro ověření dostatečné podmínky v bodech
ležících na kružnici x2
+ y2
= 1, budeme funkci z považovat za funkci jedné proměnné
t = x2
+ y2:
z = te−t, pro kterou je
bod t = 1 stacionárním bodem. Protože z
 = (t
− 2)e−t je pro
t =
1 záporná, má zde funkce z maximum. Tedy funkce z(x,y) má
neostré maximum zmax
= e−1 v bodech
kružnice x2 +
y2 = 1
(obr. 14.11
).
= (t
− 2)e−t je pro
t =
1 záporná, má zde funkce z maximum. Tedy funkce z(x,y) má
neostré maximum zmax
= e−1 v bodech
kružnice x2 +
y2 = 1
(obr. 14.11
).
> plot3d(z(x,y), x=-3..3, y=-3..3, axes=boxed,
> grid=[50,50], style=hidden, labels=[x,y,’z’],
> color=black);
> plot3d(z(x,y), x=-1..3, y=-1..3, axes=boxed,
> grid=[40,40], style=hidden, orientation=[-69,47],
> labels=[x,y,’z’], color=black);
Poznámka 14.3.
Funkce
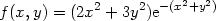
má ostré lokální minimum v bodě
[0,0],
ostré lokální maximum v bodě
[0,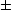 1]
1] a sedlové body
v bodech
[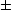 1,0]
1,0].
Absolutní extrém této funkce na kruhu
M =
{[x,y]

 2
: x2
+ y2
≤ 4}
2
: x2
+ y2
≤ 4} byl
řešen v příkladu
6.6
-ii).
Často opakované postupy při hledání lokálních
extrémů funkce dvou proměnných je možné opět automatizovat pomocí
Mapleovského programovacího jazyka. Ukázkou možného řešení jsou
procedury sing a mvextrem, jedinými parametry
těchto procedur jsou funkce, jejíž stacionární body, resp. lokální
extrémy, určujeme.
> sing:= proc( f) local cp;
> cp:={solve( { diff(f,x)=0, diff(f,y)=0}, { x, y})};
> RETURN(cp)
> end:
> mvextrem:= proc( f) local zxx,zyy,zxy,D,i,p2,pom;
> zxx:= diff( f, x, x);
> zyy:= diff( f, y, y);
> zxy:= diff( f, x, y);
> pom:=map(allvalues,sing(f));
> pom:=takereal(pom);
> for i from 1 to nops(pom) do
> p2:=op(i, pom);
> D:=
> evalf(subs(p2,zxx)*subs(p2,zyy)-subs(p2,zxy)^2);
> if D=0 then print( p2, ‘ nelze rozhodnout‘ );
> elif D<0 then print( p2, ‘ extrem nenastava‘ );
> else
> if evalf(subs( p2, zxx )) > 0 then
> print( p2,‘ lokalni minimum‘ );
> else print( p2,‘ lokalni maximum‘);
> fi;
> fi;
> od;
> end:
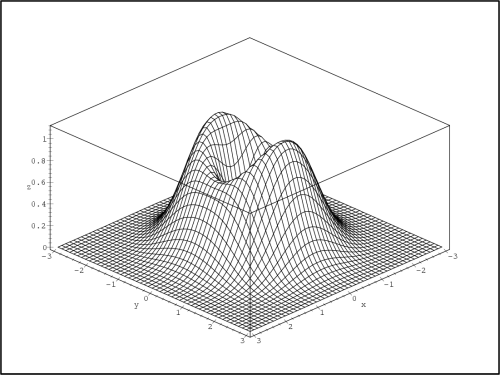
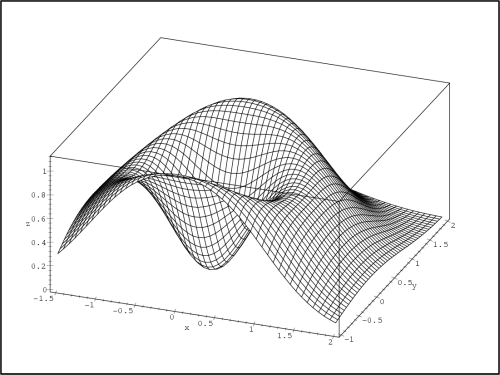
Příklad 14.6. Určete lokální extrémy funkce
z = x4
+y4
−x2
−2xy
−y2.
K řešení použijeme připravených procedur:
> mvextrem( x^4+ y^4- x^2-2*x*y-y^2);
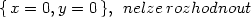
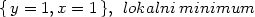
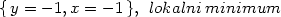
Ve stacionárním bodě [0,0] je
Δ = 0, proto o existenci
extrému v tomto bodě nelze standardním způsobem
rozhodnout.
Řešení však můžeme získat následujícím způsobem:
funkci z upravíme na tvar
z(x,y) =
x4 +
y4 −
(x +
y)2.
Odtud z(−x,x) =
2x4 >
0 pro x≠0. Na
druhé straně z(x,0) =
x4 −
x2 =
x2(1
− x2)
< 0 pro x
 (−1,0)
(−1,0)
 (0,1).
Tedy v libovolně malém okolí bodu [0,0]
funkce z nabývá jak kladných,
tak záporných hodnot, což spolu s faktem, že z(0,0) = 0
znamená, že v tomto bodě lokální extrém nenastává
(obr. 14.15
a 14.16
).
(0,1).
Tedy v libovolně malém okolí bodu [0,0]
funkce z nabývá jak kladných,
tak záporných hodnot, což spolu s faktem, že z(0,0) = 0
znamená, že v tomto bodě lokální extrém nenastává
(obr. 14.15
a 14.16
).
> plot3d(z(x,y), x=-2..2, y=-2..2, view=-3..5,
> axes=boxed, style=patch, labels=[x,y,’z’],
> orientation=[-64,51]);
> contourplot(z(x,y), x=-2..2, y=-2..2, axes=boxed,
> grid=[100,100], color=black, contours=20);
Následující příklad ilustruje situaci, kdy je
matice druhých derivací dané funkce ve stacionárním bodě pouze
semidefinitní. V tomto případě je f
 (0,0) = 0.
Proto zde může i nemusí nastat lokální extrém, viz
Poznámka 6.4
.
(0,0) = 0.
Proto zde může i nemusí nastat lokální extrém, viz
Poznámka 6.4
.
Příklad 14.7. Rozhodněte, zda funkce f(x,y) =
x3 +
y2 a g(x,y) =
x2 +
y4 mají v bodě [0,0]
extrém.
> f:=(x,y)->x^3+y^2;
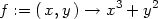
Ověřme, že bod [0,0] je
stacionárním bodem:
> cp:=sing(f(x,y));
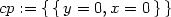
Dále:
> fxx:=D[1,1](f):fxy:=D[1,2](f):fyy:=D[2,2](f):
> Delta:=unapply(fxx(x,y)*fyy(x,y)-(fxy(x,y))^2,x,y);
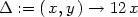
> subs(cp[1], Delta(x,y));
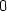
Protože Δ = 0,
nemůžeme tímto způsobem o existenci extrému rozhodnout.
Generujme však PC-grafy uvažované funkce a jejich vrstevnic
(obr. 14.17
a 14.18
).
> plot3d(f(x,y), x=-2..2, y=-2..2, axes=framed,
> orientation=[80,80], style=patch, labels=[x,y,’z’]);
> contourplot(f(x,y), x=-2..2, y=-2..2, axes=boxed,
> grid=[100,100], contours=20, color=black);
Podle PC-grafů předpokládáme, že v bodě
[0,0]
extrém nenastává. Tuto hypotézu nyní ověříme výpočtem. Platí
f(0,x) =
x2 >
0 pro x≠0, ale
zároveň platí f(x,0) =
x3 <
0 pro x  (−
(− ,0).
Tedy v libovolném okolí bodu [0,0]
funkce f nabývá jak
kladných, tak záporných hodnot, což spolu s faktem, že
f(0,0) = 0
znamená, že v tomto bodě lokální extrém nenastává.
,0).
Tedy v libovolném okolí bodu [0,0]
funkce f nabývá jak
kladných, tak záporných hodnot, což spolu s faktem, že
f(0,0) = 0
znamená, že v tomto bodě lokální extrém nenastává.
Analogicky:
> g:=(x,y)->x^2+y^4;
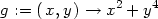
> plot3d(g(x,y), x=-2..2, y=-2..2, axes=framed,
> orientation=[60,70], style=patch, labels=[x,y,z]);
> contourplot(g(x,y), x=-2..2, y=-2..2, axes=boxed,
> grid=[100,100], contours=20, color=black);
> cp:=sing(g(x,y));
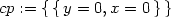
> subs(cp[1], Delta(x,y));

Přírůstek funkce g(x,y)
− g(0,0) =
x4 +
y2 >
0, tedy g má v bodě [0,0]
lokální minimum.
Závěrem si ukážeme jednu z možností, jak
pomocí Maplu generovat větší množství příkladů k ilustraci
problematiky lokálních extrémů funkce dvou proměnných. Využijeme
k tomu „symbolického zápisu funkce dvou proměnných
s parametry“, konkrétně v našem příkladu se třemi
parametry:
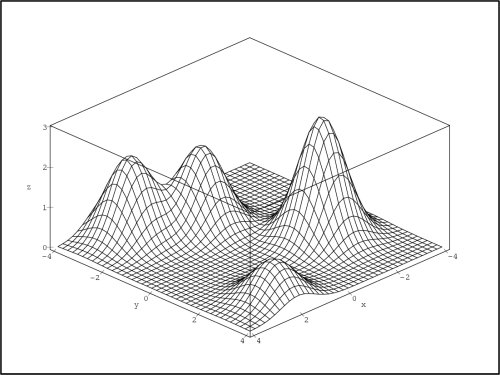
> ff:=(a,b,c)->c*exp(-(x-a)^2-(y-b)^2);
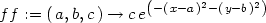
> z1:=ff(2,3,1)+ff(2,-3,2)+ff(0,-2,2)+ff(-2,1,3);
> plot3d(z1, x=-4..4, y=-4..4, axes=boxed, color=black,
> grid=[40,40], labels=[x,y,z], style=hidden,
> tickmarks=[5,5,4]);
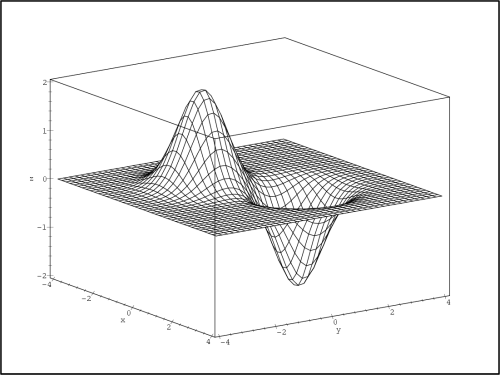
> z2:=ff(1,1,-2)+ff(-1,-1,2);
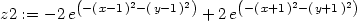
> plot3d(z2, x=-4..4, y=-4..4, axes=boxed, color=black,
> grid=[40,40], orientation=[-35,70], labels=[x,y,z],
> style=hidden);
Takto generované PC-grafy jsou názornější než
u prozatím častěji k demonstracím vlastností funkcí dvou
proměnných používaných kvadratických a kubických funkcí. Srovnejme
proto předcházející dva PC-grafy (obr. 14.21 a 14.22) např.
s PC-grafem funkce z
= x3
− 3x2
+ y3
− 3y
+ 1:
> z:=x^3-3*x^2+y^3-3*y+1;
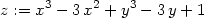
> plot3d(z, x=-3..3, y=-3..3, style=patchcontour,
> axes=boxed, orientation=[-122,-150],
> labels=[x,y,’z’]);
> plot3d(z, x=-3..3, y=-3..3, view=-6..4,
> style=patchcontour, axes=boxed,
> orientation=[-122,-150], labels=[x,y,’z’]);
Z PC-grafu na obr. 14.23 není patrné, že
uvažovaná kubická funkce z má
dva sedlové body a jedno lokální maximum a jedno lokální minimum.
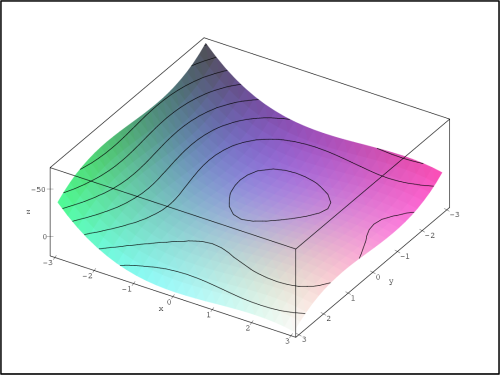
Až po dalším „zjemnění“ rozsahu zobrazovaných hodnot dostáváme
PC-graf (obr. 14.24
), který lépe ilustruje problematiku
lokálních extrémů.
Z příkladů uvedených v této části tedy
mimo jiné plyne, že pro názornější demonstraci lokálních vlastností
funkcí dvou proměnných pomocí PC-grafů jsou výhodnější
exponenciální funkce, na rozdíl od příkladů sloužících
k početnímu hledání lokálních extrémů, kde se naopak více hodí
polynomiální funkce.
14.2 Absolutní extrémy
Ukážeme si opět několik možností, jak pomocí
Maplu hledat absolutní extrémy funkcí dvou proměnných.
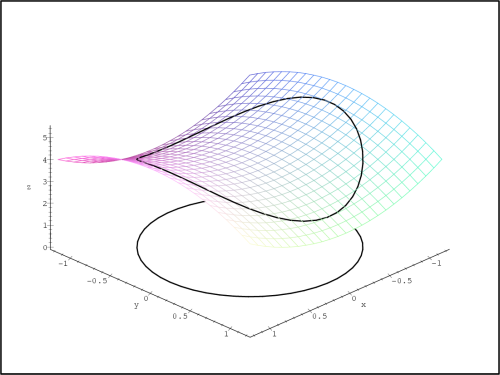
Příklad 14.8. Určete nejmenší a největší
hodnotu funkce z = f(x,y) =
x2 −
y2 + 4 na
množině M = {[x,y]

 2
: x2
+ y2
≤ 1}.
2
: x2
+ y2
≤ 1}.
Definujme nejdříve funkci f a
množinu M a poté generujme
jejich PC-grafy s cílem demonstrovat PC-graf funkce
f na množině M:
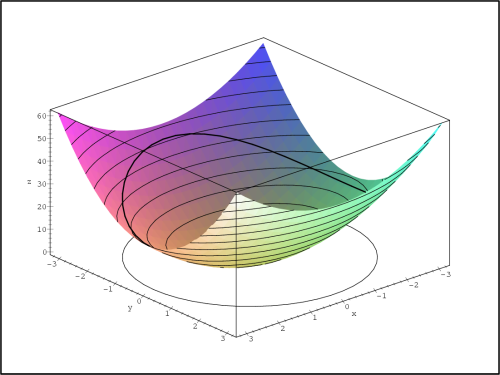
> f:=(x,y)->x^2-y^2+4;
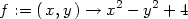
> M:=x^2+y^2=1;
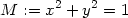
> p1:=plot3d(f(x,y), x=-1.2..1.2, y=-1.2..1.2,
> axes=framed, orientation=[31,56]):
> p2:=spacecurve([cos(t), sin(t), f(cos(t), sin(t))],
> t=0..2*Pi, color=black, thickness=3,
> orientation=[31,56]):
> p3:=spacecurve([cos(t), sin(t), 0], t=0..2*Pi,
> color=black, thickness=3, orientation=[31,56]):
> display3d({p1,p2,p3}, labels=[x,y,z]);
> p4:=spacecurve([cos(t),sin(t),f(cos(t),sin(t))+0.01],
> t=0..2*Pi, color=black, thickness=3,
> orientation=[31,56]):
> display3d({p1,p3,p4}, labels=[x,y,z]);
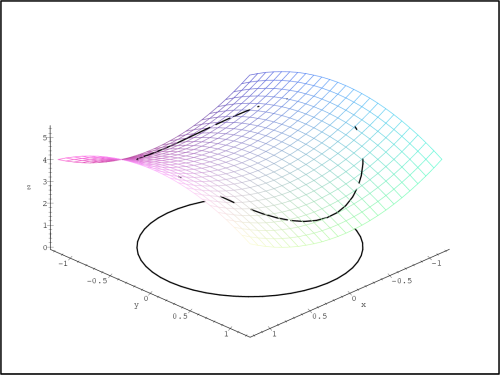
Poznámka 14.4. Všimněme si rozdílu
u těchto dvou PC-grafů. Problémem je počítačové znázornění
křivky tvořící hranici obrazu množiny M na ploše PC-grafu funkce f (p3,
obr. 14.25
). Aby byla situace názornější,
dopustíme se „malého podvodu“ a PC-graf křivky posuneme „kousek“
nad PC-graf funkce f
(p4, obr. 14.26).
Přejděme nyní ke standardnímu postupu hledání
absolutních extrémů funkce f.
Určeme nejdříve stacionární body ležící uvnitř
M:
> with(mvcalp):
> sing(f(x,y));

Dostáváme stacionární bod [0,0]
 M.
M.
> f(0,0);
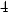
Nakonec vyšetřeme chování funkce f na hranici množiny M. Tuto hranici tvořenou kružnicí
x2 +
y2 = 1 si
rozdělme na dvě části, na horní a dolní půlkružnici:
> with(student):
> r:=isolate(M,y);
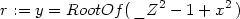
> r:=allvalues(r);
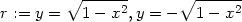
Dosazením těchto hodnot do vzorce definujícího
funkci f, dostaneme funkci
jedné reálné proměnné:
> u1:=unapply(subs(r[1], f(x,y)), x);
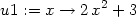
Ta popisuje projekci uvažované množiny do roviny
xy (viz. obrázek 14.26). Hledejme nyní
absolutní extrémy takto konstruované funkce jedné proměnné pro
x  [−1,1]:
[−1,1]:
> solve(diff(u1(x), x)=0, x);
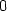
> u1(0);
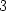
> u1(-1);u1(1);


Pro druhý případ, kdy y =
−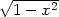 ,
x
,
x  [−1,1] je
situace stejná, neboť f(x,−y) =
f(x,y).
Porovnáním funkčních hodnot funkce f na hranici množiny M s funkční hodnotou
funkce f v jejím
jediném stacionárním bodě [0,0]
dojdeme k závěru, že
[−1,1] je
situace stejná, neboť f(x,−y) =
f(x,y).
Porovnáním funkčních hodnot funkce f na hranici množiny M s funkční hodnotou
funkce f v jejím
jediném stacionárním bodě [0,0]
dojdeme k závěru, že
| fmin = 3 |
pro [x,y] =
[0,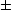 1] 1] |
|
|
| fmax = 5 |
pro [x,y] =
[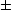 1,0]. 1,0]. |
|
|
Poznámka 14.5. K výpočtu extrémů funkce
f na hranici množiny
M můžeme také použít přímo
příkazu extrema(expr,constraints,<vars>,’s’).
Například pro předchozí situaci:
> extrema(f(x,y), M, {x,y}, ’body’);

> body;
Příkaz extrema dává na
výstupu maximální a minimální hodnotu funkce f na hranici množiny M a do proměnné ’s’ ukládá souřadnice bodů, ve
kterých maximum a minimum nastává. Využívá k tzv. hledání
vázaných extrémů známé metody Lagrangeových multiplikátorů
(Věta 9.1
). Příkaz extrema ale většinou používáme
pouze ke kontrole výpočtů, protože podstata metody Langrangeových
multiplikátorů při jeho použití zůstává skryta (viz
příklad 14.12
).
Při řešení dalšího příkladu budeme ilustrovat
postup stejný jako při výpočtu pomocí „tužky a papíru“, pouze zápis
budeme provádět formou Mapleovských příkazů.
Příklad 14.9. Najděte absolutní extrémy
funkce z = x2
+ 2xy −
4x +
8y v obdélníku
určeném přímkami y = 0, x
= 0, x = 1 a
y =
2.
> z:=(x,y)->x^2+2*x*y-4*x+8*y;
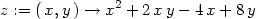
Určeme stacionární body funkce z:
> with(mvcalp):
> sing(z(x,y));
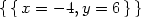
Získaný bod [−4,6] však
nepatří do vyšetřovaného obdélníku.
Vyšetřeme nyní funkci z na hranici obdélníku, tj. na úsečkách
y =
0, x  [0,1],
x =
0, y
[0,1],
x =
0, y  [0,2],
y =
2, x
[0,2],
y =
2, x  [0,1] a
x =
1, y
[0,1] a
x =
1, y  [0,2].
[0,2].
Dosazením dostáváme:
> u1:=unapply(subs(y=0, z(x,y)), x);
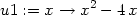
a hledáme absolutní extrémy této funkce jedné
proměnné na intervalu [0,1]:
> solve(diff(u1(x), x)=0, x);
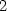
Ani tento stacionární bod nepatří do intervalu
[0,1] a
vyšetříme tedy pouze funkční hodnoty v krajních bodech
intervalu:
> u1(0);u1(1);
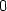
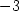
Obdobně postupujeme i na zbývajících
úsečkách:
> u2:=unapply(subs(x=0, z(x,y)), y);
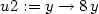
> solve(diff(u2(y), y)=0, y);
> u2(0);u2(2);
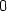
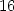
> u3:=unapply(subs(y=2, z(x,y)), x);
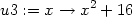
> solve(diff(u3(x), x)=0, x);
> u3(0);u3(1);
> u4:=unapply(subs(x=1, z(x,y)), y);
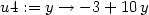
> solve(diff(u4(y), y)=0, y);
> u4(0);u4(2);
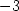
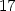
Porovnáním získaných funkčních hodnot funkce
z na hranici vidíme, že
| fmin |
=
−3 |
pro [x,y] |
=
[1,0] |
|
|
|
|
| fmax |
= 17 |
pro [x,y] |
=
[1,2]. |
|
|
|
|
Graficky je příklad znázorněn na obr.
14.27. Grafické
znázornění zde slouží pro kontrolu získaných výsledků.
> plot3d(z(x,y), x=0..1, y=0..2, axes=boxed,
> orientation=[-21,3], color=black, tickmarks=[2,5,6],
> scaling=constrained, labels=[x,y,’z’]);
Závěrem si ještě ukažme metodu, jak lze řešit
úlohy na absolutní extrémy v některých speciálních případech,
např. umíme-li sestrojit vrstevnice funkce, jejíž extrémy hledáme,
a pokud množina, kde tyto extrémy hledáme je „dostatečně
jednoduchá“.
Příklad 14.10. Najděte nejmenší a největší hodnotu funkce
f(x,y) =
x − y na
množině M : x2
+ y2
≤ 1.
Generujme PC-grafy funkce f a
vrstevnic funkce f spolu
s množinou M:
> f:=(x,y)->x-y;
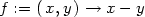
> v1:=plot3d(f(x,y), x=-3..3, y=-3..3,
> style=patchcontour, axes=boxed, contours=20):
> v2:=spacecurve([cos(t), sin(t), f(cos(t), sin(t))],
> t=0..2*Pi, color=black, thickness=3):
> v3:=spacecurve([cos(t), sin(t), -6],t=0..2*Pi,
> color=black, thickness=3):
> display3d({v1,v2,v3}, axes=boxed, labels=[x,y,’z’],
> scaling=constrained, orientation=[19,31]);
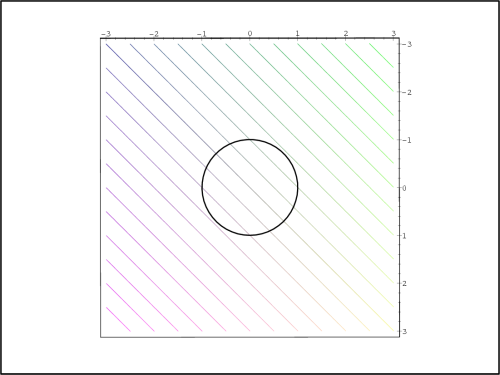
> v4:=plot3d(f(x,y), x=-3..3, y=-3..3, style=contour,
> axes=boxed, contours=20, grid=[100,100]):
> display3d({v2,v4}, orientation=[0,0],
> scaling=constrained);
> f(1/sqrt(2),-1/sqrt(2));f(-1/sqrt(2),1/sqrt(2));
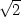
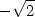
Vrstevnice funkce f jsou přímky x −
y = c (viz
ilustrace na obr. 14.28
). Z PC-grafu na
obrázku 14.29
(vrstevnice – osa x je zde svislá, y vodorovná) je také vidět, že podmínkou
pro to, aby hodnota c

 byla hodnotou absolutního maxima resp.
minima funkce f je, že přímka
x − y
= c je tečnou ke kružnici x2
+ y2
= 1. Z PC-grafů je zřejmé,
že maximum nastane v bodě [
byla hodnotou absolutního maxima resp.
minima funkce f je, že přímka
x − y
= c je tečnou ke kružnici x2
+ y2
= 1. Z PC-grafů je zřejmé,
že maximum nastane v bodě [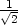 ,
,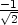 ], jeho hodnota je
], jeho hodnota je 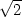 a
minimum je v bodě [
a
minimum je v bodě [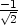 ,
,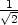 ], jeho hodnota je −
], jeho hodnota je −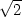 (viz příklad 6.7
-ii)).
(viz příklad 6.7
-ii)).
Příklad 14.11. Najděte nejmenší a největší
hodnotu funkce z = f(x,y) =
2x2 +
4y2 na množině M :
x2 +
y2 ≤
9.
Postupujme stejně jako v předcházejícím příkladě:
> z:=(x,y)->2*x^2+4*y^2;
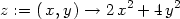
> o1:=plot3d(z(x,y), x=-3.2..3.2, y=-3.2..3.2,
> style=patchcontour):
> o2:=spacecurve([3*cos(t), 3*sin(t), z(3*cos(t),
> 3*sin(t))+0.1], t=0..2*Pi, color=black, thickness=3):
> o3:=spacecurve([3*cos(t), 3*sin(t), 0], t=0..2*Pi,
> color=black, thickness=2):
> o4:=plot3d(z(x,y),x=-3.2..3.2,y=-3.2..3.2,
> style=contour, axes=normal):
> display3d({o1,o2,o3},orientation=[49,53],
> axes=boxed, labels=[x,y,’z’]);
> display3d({o4,o2}, orientation=[0,0],
> scaling=constrained, axes=framed, labels=[x,y,z]);
> z(0,0);z(0,3);z(0,-3);
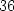
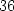
S pomocí PC-grafů (obr. 14.30 a
obr. 14.31
) není obtížné určit, že
| zmin |
= 0 |
pro [x,y]
= |
[0,0] |
|
|
|
|
| zmax |
= 36 |
pro [x,y]
= |
[0,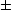 3]. 3]. |
|
|
|
|
14.3 Vázané extrémy
V následujícím příkladě hledáme extrémy na
hranici množiny M metodou
Langrangeových multiplikátorů bez použití příkazu extrema.
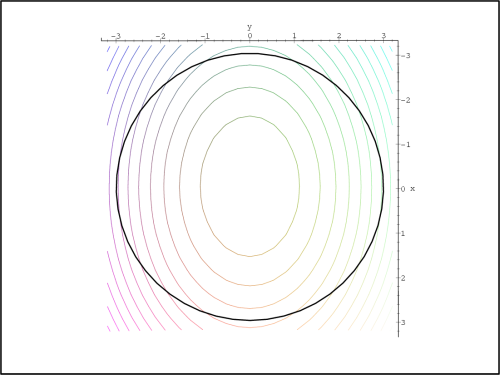
Příklad 14.12. Určete největší a nejmenší hodnotu funkce
z = f(x,y) =
2x2 −
2xy +
y2 na množině M =
{[x,y]

 2
: x2
+ y2
≤ 1}.
2
: x2
+ y2
≤ 1}.
> f := (x,y) -> 2*x^2 - 2*x*y + y^2;

> g:=(x,y)->x^2+y^2-1;
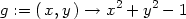
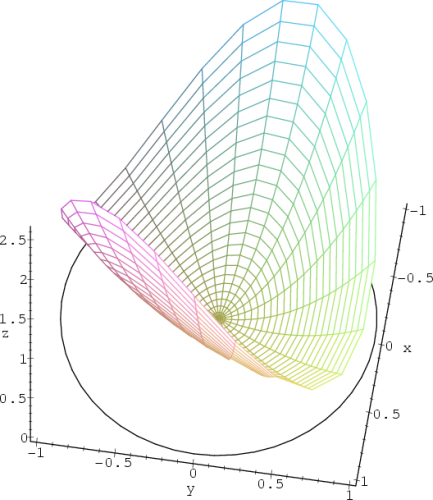
Nejdříve opět generujme PC-graf
funkce f na
množině M
(obr. 14.32
):
> g1:=cylinderplot([r,theta,f(r*cos(theta),
> r*sin(theta))], r=0..1, theta=0..2*Pi,
> scaling=constrained):
> g2:=spacecurve([cos(t), sin(t), 0], t=0..2*Pi,
> color=black, scaling=constrained):
> display3d({g1,g2}, axes=framed, orientation=[9,30],
> scaling=constrained, labels=[x,y,’z’]);
Dále určeme stacionární body funkce f ležící uvnitř množiny M:
> sing(f(x,y));
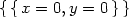
> f(0,0);
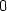
Na závěr, k určení extrémů funkce
f na hranici množiny
M použijeme metodu
Lagrangeových multiplikátorů. Sestavme Lagrangeovu funkci
úlohy:
> F:=unapply(f(x,y)-lambda*g(x,y),x,y,lambda);
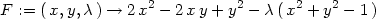
V souladu se standardním postupem vytvořme
(s použitím parciálního derivování Lagrangeovy
funkce F podle všech
proměnných) pomocný systém podmínek pro stacionární body naší
úlohy:
> eq1:=diff(F(x,y,lambda),x)=0;
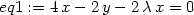
> eq2:=diff(F(x,y,lambda),y)=0;
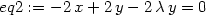
> eq3:=g(x,y)=0;

Symbolické řešení této soustavy rovnic:
> solve({eq1,eq2,eq3}, {x,y,lambda});
však není vhodné pro další výpočty (opět se jen těžko
interpretuje), použijeme proto řešení numerické:
> sol:=fsolve({eq1,eq2,eq3},{x,y,lambda},
maxsols=10);
Pro takto získané hodnoty
x,
y,

dopočítejme funkční hodnoty funkce
f:
> for i from 1 to nops([sol]) do
> subs(op(i,[sol]), [x,y]); subs(op(i, [sol]), f(x,y))
> od;
![[− .5257311121,− .8506508084 ]](diferencialni-pocet1640x.png)

![[.5257311121,.8506508084 ]](diferencialni-pocet1642x.png)

![[.8506508084,− .5257311121]](diferencialni-pocet1644x.png)
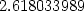
![[− .8506508084,.5257311121]](diferencialni-pocet1646x.png)
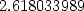
Výsledek znázorněme na PC-grafu funkce
f (obr. 14.33):
> pts:=pointplot({seq(subs(op(i,[sol]),
[x,y,f(x,y)]),
> i=1..nops([sol]))}, color=black, symbol=box):
> display3d({g1,g2,pts}, axes=framed,
> orientation=[135,70], scaling=constrained,
> labels=[x,y,’z’]);
Porovnáním získaných funkčních hodnot
s funkční hodnotou ve stacionárním bodě dostáváme, že
| fmin |
= 0 |
pro [x,y] |
=
[0,0] |
|
|
|
|
| fmax |
≐2.618 |
pro [x,y] |
≐[0.851,−0.526] a
[x,y]≐[−0.851,−0.526]. |
|
|
|
|
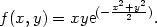
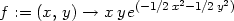
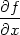
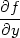
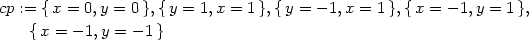
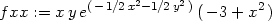
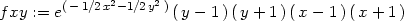
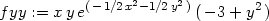
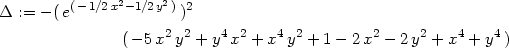
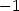
![[ ] 4 (e(−1))2,− 2e(−1)](diferencialni-pocet1471x.png)
![[ ] 4 (e(−1))2,2e(−1)](diferencialni-pocet1472x.png)
![[ (−1) 2 (−1)] 4 (e ) ,− 2e](diferencialni-pocet1473x.png)
![[ ] 4 (e(−1))2,2e(−1)](diferencialni-pocet1474x.png)
![(−1) (−1 ) (−1) (−1) [e ,− e ,e ,− e ]](diferencialni-pocet1475x.png)
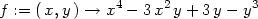
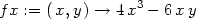
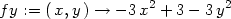
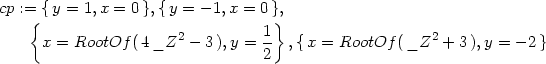
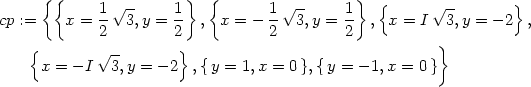
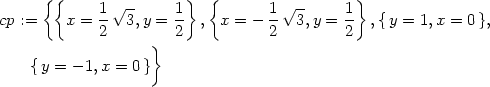
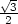

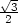

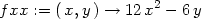
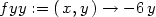
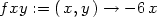
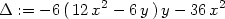
![{ } x = 1-√3,y = 1- ,[− 45,6 ] 2 2](diferencialni-pocet1490x.png)
![{ } x = − 1-√3,y = 1- ,[− 45,6 ] 2 2](diferencialni-pocet1491x.png)
![{x = 0,y = 1},[36,− 6]](diferencialni-pocet1492x.png)
![{x = 0,y = − 1 },[36,6]](diferencialni-pocet1493x.png)
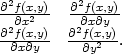
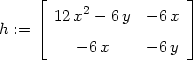
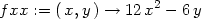
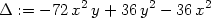
![{x = 0,y = 1},[36,− 6]](diferencialni-pocet1500x.png)
![{x = 0,y = − 1 },[36,6]](diferencialni-pocet1501x.png)
![{ 1 1 √ -} y = -,x = -- 3 ,[− 45,6 ] 2 2](diferencialni-pocet1502x.png)
![{ 1 1 √ -} y = -,x = − -- 3 ,[− 45,6 ] 2 2](diferencialni-pocet1503x.png)
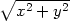 .
.
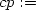


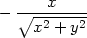
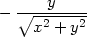
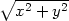 je záporný, tedy podle definice v bodě
je záporný, tedy podle definice v bodě 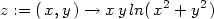
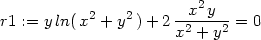
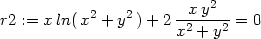
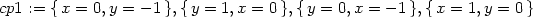
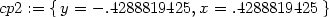
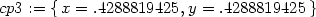
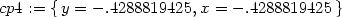
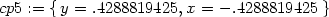
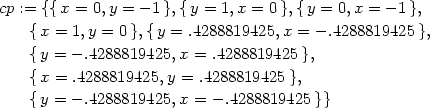
![{x = 0,y = − 1 },[− 4,0]](diferencialni-pocet1522x.png)
![{y = 1,x = 0 },[− 4,0 ]](diferencialni-pocet1523x.png)
![{y = 0,x = − 1 },[− 4,0]](diferencialni-pocet1524x.png)
![{x = 1,y = 0 },[− 4,0 ]](diferencialni-pocet1525x.png)
![{y = .4288819425,x = − .4288819425 },[4.,− 2.]](diferencialni-pocet1526x.png)
![{y = − .4288819425, x = .4288819425 },[4.,− 2.]](diferencialni-pocet1527x.png)
![{x = .4288819425, y = .4288819425 },[4.,2.]](diferencialni-pocet1528x.png)
![{y = − .4288819425, x = − .4288819425 },[4.,2.]](diferencialni-pocet1529x.png)
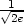
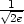
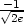
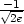
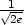
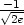
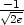
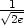
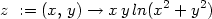
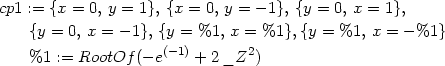

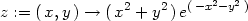
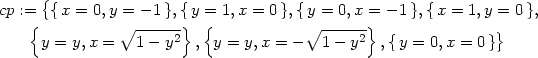
![{y = 0,x = 1},[0,− 4e(−1)]](diferencialni-pocet1543x.png)
![{y = 0,x = − 1},[0,− 4 e(−1)]](diferencialni-pocet1544x.png)
![{ ∘ ------} x = x,y = 1 − x2 ,[0,− 4x2 e(−1)]](diferencialni-pocet1545x.png)
![{ ∘ -----2} 2 (−1) x = x,y = − 1− x ,[0,− 4x e ]](diferencialni-pocet1546x.png)
![{y = 0,x = 0 },[4,2 ]](diferencialni-pocet1547x.png)
![{x = 0,y = 1 },[0,0 ]](diferencialni-pocet1548x.png)
![{x = 0,y = − 1},[0,0 ]](diferencialni-pocet1549x.png)

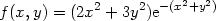

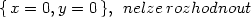
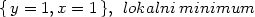
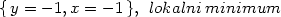



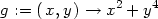
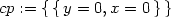

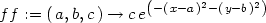
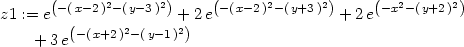
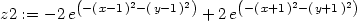
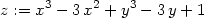
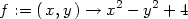
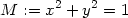

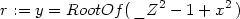
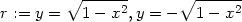
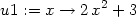
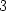


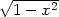 ,
,

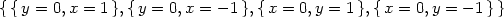
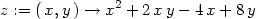
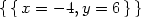
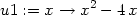
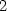
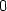
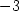
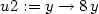
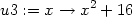
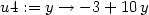
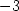
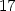
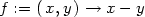
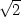
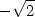
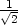
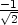
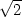 a
minimum je v bodě
a
minimum je v bodě 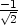
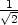
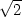 (viz příklad
(viz příklad 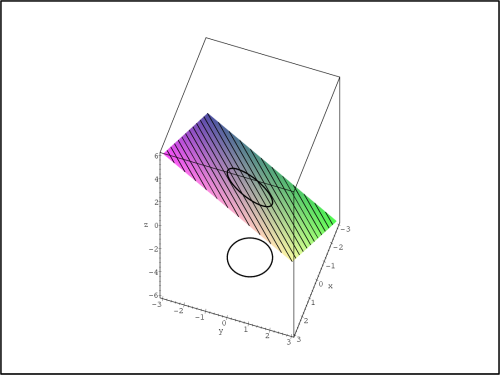
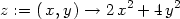

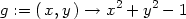
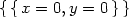
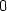
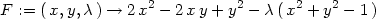
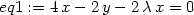

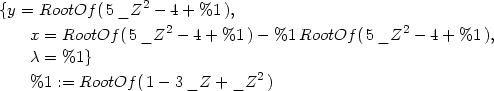
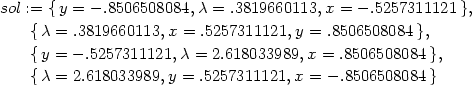

![[− .5257311121,− .8506508084 ]](diferencialni-pocet1640x.png)

![[.5257311121,.8506508084 ]](diferencialni-pocet1642x.png)

![[.8506508084,− .5257311121]](diferencialni-pocet1644x.png)
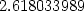
![[− .8506508084,.5257311121]](diferencialni-pocet1646x.png)