 n
zavést metriku. Proto připomeňme několik základních pojmů
z teorie metrických prostorů.
n
zavést metriku. Proto připomeňme několik základních pojmů
z teorie metrických prostorů.[Další] [Předchozí] [Předchozí – na konec] [Na konec] [Výše]
Pojem limity funkce patří k základním pojmům diferenciálního počtu. Je to lokální vlastnost funkce, popisující chování funkce v ryzím okolí bodu, v němž limitu určujeme. (Ryzím okolím bodu rozumíme okolí kromě tohoto bodu.) Skutečnost, že jde o ryzí, okolí znamená, že limita nezávisí na funkční hodnotě funkce v tomto bodě – funkční hodnota se může lišit od limity v tomto bodě nebo funkce nemusí být v daném bodě vůbec definována.
Rovněž pojem spojitosti funkce více proměnných lze podobně jako pro funkce jedné proměnné definovat pomocí limity funkce, proto zde najdeme řadu tvrzení podobných těm, se kterými jsme se již setkali v diferenciálním počtu funkcí jedné proměnné.
K definici limity, spojitosti a všech dalších
pojmů diferenciálního počtu je třeba na  n
zavést metriku. Proto připomeňme několik základních pojmů
z teorie metrických prostorů.
n
zavést metriku. Proto připomeňme několik základních pojmů
z teorie metrických prostorů.
 n
nPřipomeňme, že  -okolí vlastního bodu a
-okolí vlastního bodu a 
 lze zapsat jako interval
lze zapsat jako interval  x
− a
x
− a <
<  ,
,  >
0. Okolí
>
0. Okolí  (a) bodu
a
(a) bodu
a 
 n je
definováno pomocí metriky
n je
definováno pomocí metriky  v
v  n jako množina
n jako množina
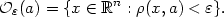
 vynechávat.
vynechávat.
Podle výběru metriky dostáváme různé typy okolí.
Např. v  2 dostaneme kruhové okolí, zvolíme-li
euklidovskou metriku
2 dostaneme kruhové okolí, zvolíme-li
euklidovskou metriku
![ρ ([x ,y ],[x ,y ]) = ∘(x--−-x-)2-+-(y--−-y-)2, 2 1 1 2 2 1 2 1 2](diferencialni-pocet95x.png)
![ρ∞([x1,y1],[x2,y2]) = max{ ∣x1 − x2∣,∣y1 − y2∣},](diferencialni-pocet96x.png)
![ρ1([x1,y1],[x2,y2]) = ∣x1 − x2∣ + ∣y1 − y2∣.](diferencialni-pocet97x.png)
Z důvodu formální jednoduchosti zvolme
v této kapitole maximální metriku, ve které je okolí bodu
a =
[a1,…,an]

 n
kartézským součinem okolí jednotlivých souřadnic a1,…,an,
tj.
n
kartézským součinem okolí jednotlivých souřadnic a1,…,an,
tj.
![𝒪ɛ(a) = {x = [x1,...,xn] ∈ ℝn : max ∣xi − ai∣ < ɛ}. 1≤i≤n](diferencialni-pocet98x.png)
 (a)
(a)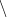 {a}.
{a}.
Okolí nevlastních
bodů v  2 jsou
definována v souladu
s maximální metrikou takto:
Okolím nevlastního bodu
[
2 jsou
definována v souladu
s maximální metrikou takto:
Okolím nevlastního bodu
[ ,
, ]
rozumíme libovolnou
množinu typu
(a,
]
rozumíme libovolnou
množinu typu
(a, )
)
 (b,
(b, ), a,b
), a,b 
 . Analogicky definujeme okolí nevlastního bodu
[−
. Analogicky definujeme okolí nevlastního bodu
[− ,
, ], [
], [ ,−
,− ], [−
], [− ,−
,− ], i okolí
bodů
typu [a,
], i okolí
bodů
typu [a,
 ],[
],[
 ,a]. Okolí nevlastních
bodů v prostorech
vyšších dimenzí
jsou definována analogicky.
Množinu
,a]. Okolí nevlastních
bodů v prostorech
vyšších dimenzí
jsou definována analogicky.
Množinu  n
spolu s nevlastními body budeme
označovat (
n
spolu s nevlastními body budeme
označovat ( ∗)n.
∗)n.
V definici limity vystupují funkční hodnoty funkce v ryzím
(libovolně malém) okolí
bodu, v němž limitu definujeme.
Z tohoto důvodu lze limitu
funkce vyšetřovat jen
v hromadných bodech
definičního oboru. Proto, aniž bychom tento fakt
stále
zdůrazňovali, budeme ve všech
kapitolách, kde se vyskytuje
limita funkce v daném
bodě,
předpokládat,
že tento bod
je hromadným bodem
množiny 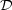 (f) (připomeň
me, že bod x
(f) (připomeň
me, že bod x

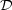 (f) je hromadným bodem
množiny
(f) je hromadným bodem
množiny 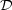 (f),
jestliže každé jeho ryzí
okolí
obsahuje alespoň
jeden bod této
množiny).
(f),
jestliže každé jeho ryzí
okolí
obsahuje alespoň
jeden bod této
množiny).
Limita se nazývá vlastní, jestliže
L 
 ,
v opačném případě (L
=
,
v opačném případě (L
= 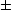
 ) se nazývá nevlastní
limita. Bod a
) se nazývá nevlastní
limita. Bod a  (
( n)∗ se
nazývá limitní bod.
n)∗ se
nazývá limitní bod.
Uvedená definice limity je univerzální definicí pro
funkci jedné či více proměnných, pro vlastní či nevlastní limitu a
pro vlastní i nevlastní limitní body. Specifikací okolí pro vlastní
limitní bod i limitu a

 n, L
n, L 
 dostáváme
tzv.
dostáváme
tzv.  −
−  definici vlastní limity ve vlastním bodě. Tuto
definici zde zformulujeme pro funkci dvou proměnných.
definici vlastní limity ve vlastním bodě. Tuto
definici zde zformulujeme pro funkci dvou proměnných.
|
Definice 2.2. Řekneme, že funkce
f : 
|
Zásadní rozdíl mezi limitou funkce jedné proměnné a limitou funkce dvou a více proměnných spočívá v „dimenzi“ okolí limitního bodu – u funkce jedné proměnné se k tomuto bodu můžeme blížit jen po přímce, tj. ze dvou stran (což znamená, že funkce má limitu v bodě, má-li obě jednostranné limity a tyto se sobě rovnají), zatímco u funkce více proměnných je těchto možností nekonečně mnoho; můžeme se blížit k danému bodu po přímkách, po parabolách či obecných množinách. Existence limity v daném bodě znamená, že nezáleží na cestě, po které se k danému bodu blížíme. Naopak dostaneme-li různé hodnoty limity pro různé cesty, znamená to, že limita v daném bodě nemůže existovat.
Příklad 2.1. i) Pomocí konkrétní specifikace okolí limitního bodu a limity definujte
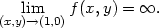
Řešení. Vzhledem
k tomu, že okolí bodu  je tvaru
(A,
je tvaru
(A, ) a ryzí
) a ryzí  -okolí bodu [1,0] je
{(1 −
-okolí bodu [1,0] je
{(1 −
 ,1 +
,1 +
 )
)
 (−
(− ,
, )}
)}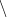 {[1,0]},
dostáváme tuto specifikaci obecné Definice 2.1: Limita lim(x,y)
{[1,0]},
dostáváme tuto specifikaci obecné Definice 2.1: Limita lim(x,y) (1,0)f(x,y) =
(1,0)f(x,y) =
 , jestliže ke každému A
, jestliže ke každému A 
 existuje
existuje  > 0
takové, že pro všechna [x,y]
> 0
takové, že pro všechna [x,y]

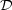 (f)
splňující
(f)
splňující  x −
1
x −
1 <
<
 ,
,  y
y <
<  , [x,y]≠[1,0]
platí f(x,y)
> A.
, [x,y]≠[1,0]
platí f(x,y)
> A.

ii) Dokažte, že funkce f(x,y) =
 má v bodě [0,0]
nevlastní limitu
má v bodě [0,0]
nevlastní limitu  .
.
Řešení. Nechť
A 
 je
libovolné. Položme
je
libovolné. Položme  =
= 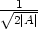 . Pro
. Pro  x
x <
<  ,
,  y
y <
<  platí x2
+ y2
< 2
platí x2
+ y2
< 2 2
=
2
= 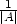 . Odtud pro [x,y]≠[0,0]
platí
. Odtud pro [x,y]≠[0,0]
platí 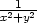 >
>
 A
A > A. Tedy k A
> A. Tedy k A 
 libovolnému jsme našli
libovolnému jsme našli  > 0
takové, že pro [x,y]≠[0,0]
splňující
> 0
takové, že pro [x,y]≠[0,0]
splňující  x
x <
<  ,
,  y
y <
<  platí
platí 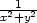 > A, tj. podle
definice limity lim(x,y)
> A, tj. podle
definice limity lim(x,y) (0,0)
(0,0) =
=  . Graf funkce
z =
. Graf funkce
z =  je znázorněn na
vedlejším obrázku.
je znázorněn na
vedlejším obrázku.
Podobně jako u funkce jedné proměnné platí následující věty o limitách funkcí. Protože definice limity funkce více proměnných pomocí okolí bodu je stejná jako pro funkci jedné proměnné, jsou i důkazy těchto tvrzení stejné jako pro funkce jedné proměnné. Čtenáři doporučujeme provést si je jako cvičení.
Věta 2.2. Nechť lim(x,y) (x0,y0)f(x,y) = 0
a funkce g je ohraničená
v nějakém ryzím okolí bodu [x0,y0] (tj.
existuje konstanta K
≥ 0 taková, že
(x0,y0)f(x,y) = 0
a funkce g je ohraničená
v nějakém ryzím okolí bodu [x0,y0] (tj.
existuje konstanta K
≥ 0 taková, že  g(x,y)
g(x,y) ≤
K v tomto ryzím okolí).
Pak
≤
K v tomto ryzím okolí).
Pak
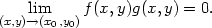
Věta 2.3. Nechť h(x,y) ≤ f(x,y) ≤ g(x,y) v nějakém ryzím okolí bodu [x0,y0] a platí


Věta 2.4. Nechť


 . Pak pro
každé c,c1,c2
. Pak pro
každé c,c1,c2

 platí
platí
![(x,y)li→m(x0,y0)cf (x,y) = cL, (x,y)→li(mx0,y0)[c1f (x, y)+ c2g(x,y)] = c1L1 + c2L2, (x,y)li→m(x0,y0)[f(x,y)g(x,y)] = L1L2.](diferencialni-pocet114x.png)
|
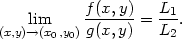
Věta 2.5. Má-li funkce f v bodě [x0,y0]
 (
( ∗)2
vlastní limitu, pak existuje ryzí okolí bodu [x0,y0],
v němž je funkce f
ohraničená.
∗)2
vlastní limitu, pak existuje ryzí okolí bodu [x0,y0],
v němž je funkce f
ohraničená.
Poznámka 2.1. Počítání limit funkcí dvou a
více proměnných je často obtížnější než v případě funkcí jedné
proměnné, neboť k počítání tzv. neurčitých výrazů (limity typu
„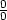 “, „
“, „ “) nemáme k dispozici
žádnou analogii l’Hospitalova1 pravidla. Proto při výpočtu limit tohoto typu
používáme různé úpravy funkce, jejíž limitu počítáme. Nejčastěji
používané úpravy jsou ukázány v následujících příkladech.
“) nemáme k dispozici
žádnou analogii l’Hospitalova1 pravidla. Proto při výpočtu limit tohoto typu
používáme různé úpravy funkce, jejíž limitu počítáme. Nejčastěji
používané úpravy jsou ukázány v následujících příkladech.
Příklad 2.2. Vypočtěte limity následujících funkcí:
i) f(x,y) =
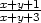 v bodě [1,0].
v bodě [1,0].
Řešení. Pokud můžeme souřadnice limitního bodu do příslušného výrazu dosadit (tj. po dosazení neobdržíme neurčitý výraz), je hodnota limity dané funkce rovna funkční hodnotě v tomto bodě. Platí tedy
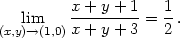
ii) f(x,y) =
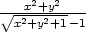 v bodě [0,0].
v bodě [0,0].
Řešení. Protože
bychom dosazením souřadnic limitního bodu získali neurčitý výraz
typu 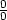 , najdeme hodnotu limity obratem typickým i pro
funkce jedné proměnné. Čitatele i jmenovatele zlomku vynásobíme
výrazem
, najdeme hodnotu limity obratem typickým i pro
funkce jedné proměnné. Čitatele i jmenovatele zlomku vynásobíme
výrazem 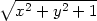 + 1. Po této úpravě dostáváme
+ 1. Po této úpravě dostáváme
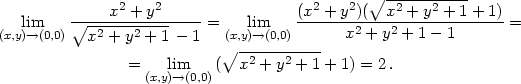
|
iii) f(x,y) =
(x + y)sin sin
sin v bodě [0,0].
v bodě [0,0].
Řešení. Protože
lim(x,y) (0,0)(x
+ y) = 0 a
(0,0)(x
+ y) = 0 a
 sin
sin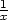 sin
sin
 ≤ 1 pro
každé [0,0]≠[x,y]
≤ 1 pro
každé [0,0]≠[x,y]

 2, je
podle Věty 2.2
lim(x,y)
2, je
podle Věty 2.2
lim(x,y) (0,0)(x
+ y)sin
(0,0)(x
+ y)sin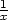 sin
sin = 0.
= 0.
iv) f(x,y) =
 v bodě (1,
v bodě (1, ).
).
Řešení. Nejprve
ukážeme, že lim(x,y) (1,
(1, )
) = 0. Nechť
= 0. Nechť
 > 0 je libovolné. Musíme najít
> 0 je libovolné. Musíme najít  > 0 a
A
> 0 a
A 
 taková, že
pro x
taková, že
pro x  (1
−
(1
− ,1 +
,1 +
 ) a
y > A platí
) a
y > A platí 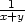 <
<  . Nechť
. Nechť
 > 0
je libovolné a položme A
=
> 0
je libovolné a položme A
=  +
+  −
1. Pak pro x
−
1. Pak pro x  (1 −
(1 −
 ,1 +
,1 +
 ), y >
A platí x + y >
1 −
), y >
A platí x + y >
1 −  +
+  − 1 +
− 1 +
 =
=  , odtud
, odtud 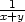 <
<  . Protože funkce cosy je
ohraničená, platí lim(x,y)
. Protože funkce cosy je
ohraničená, platí lim(x,y) (1,
(1, )
) = 0.
= 0.
v) f(x,y) = xy ln(x2 + y2) v bodě [0,0].
Řešení. Z diferenciálního počtu funkcí jedné proměnné víme, že
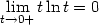
 xy
xy ≤
≤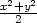 (která je ekvivalentní nerovnosti (x
(která je ekvivalentní nerovnosti (x
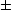 y)2
≥ 0), platí
y)2
≥ 0), platí
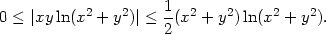 |
(2.1) |
Položme t
= x2
+ y2.
Je-li (x,y)
 (0,0), je
t
(0,0), je
t  0+, a
tedy
0+, a
tedy
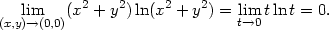
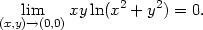
vi) f(x,y,z) =
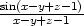 v bodě [1,1,1].
v bodě [1,1,1].
Řešení. Příklad
vyřešíme metodou substituce. Položme t =
x − y
+ z −
1. Pro (x,y,z)
 (1,1,1) je
t
(1,1,1) je
t  0.
Protože limt
0.
Protože limt 0
0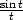 = 1, k libovolnému
= 1, k libovolnému  > 0
existuje
> 0
existuje  1 >
0 takové, že pro 0 <
1 >
0 takové, že pro 0 <
 t
t <
<  1 je
1 je
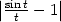 <
<
 .
Položme
.
Položme  =
= 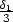 . Pak pro [x,y,z]
. Pak pro [x,y,z]

 3
splňující
3
splňující  x−
1
x−
1 <
<
 ,
,
 y
− 1
y
− 1 <
<  ,
,  z −
1
z −
1 <
<
 ,
x − y
+ z −
1≠0 je
0 <
,
x − y
+ z −
1≠0 je
0 <  x −
y + z
− 1
x −
y + z
− 1 <
<  1, a
tedy
1, a
tedy
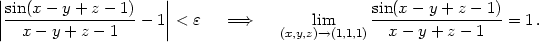
Řekli jsme, že existence limity v daném bodě
znamená, že nezáleží na cestě, po které se k danému bodu
blížíme. Naopak dostaneme-li různé hodnoty limity pro různé cesty,
znamená to, že limita v daném bodě nemůže existovat. Tohoto
faktu využíváme při důkazu neexistence limity funkce dvou
proměnných ve vlastním bodě [x0,y0]
zavedením polárních
souřadnic r, definovaných
vztahy
definovaných
vztahy


 [0,2p) je
úhel, který svírá spojnice těchto bodů s kladným směrem osy
x.
[0,2p) je
úhel, který svírá spojnice těchto bodů s kladným směrem osy
x.
Jestliže hodnota limity funkce závisí na úhlu
 , znamená to, že závisí na cestě, po
které se blížíme k danému bodu, a proto funkce nemá
v tomto bodě limitu.
, znamená to, že závisí na cestě, po
které se blížíme k danému bodu, a proto funkce nemá
v tomto bodě limitu.
Poznámka 2.2. Zavedením polárních souřadnic při výpočtu limity
vyšetřujeme chování funkce f v okolí limitního bodu [x0,y0] na
přímkách se směrovým vektorem (cos ,sin
,sin ). Pokud limita vyjde nezávisle na úhlu
). Pokud limita vyjde nezávisle na úhlu
 , je to pouze nutná podmínka pro
existenci limity v bodě [x0,y0], protože
pro jiný způsob „blížení“, např. po parabolách, můžeme obdržet
zcela odlišný výsledek. Jako příklad uvažujme funkci f :
, je to pouze nutná podmínka pro
existenci limity v bodě [x0,y0], protože
pro jiný způsob „blížení“, např. po parabolách, můžeme obdržet
zcela odlišný výsledek. Jako příklad uvažujme funkci f :
 2
2 
 definovanou takto:
definovanou takto:
![{ x2y f (x,y) = x4+y2, [x,y] ⁄= [0,0], 0, [x,y] = [0,0].](diferencialni-pocet151x.png)
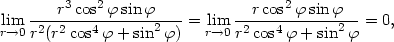
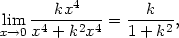
Následující věta
udává podmínku, za které
je nezávislost limity
na  po
přechodu k polárním
souřadnicím i
postačující pro existenci limity.
po
přechodu k polárním
souřadnicím i
postačující pro existenci limity.
Věta 2.6. Funkce
f má v bodě
[x0,y0] limitu rovnu L,
jestliže existuje nezáporná
funkce g : [0, )
)
 [0,
[0, )
splňující limr
)
splňující limr 0+g(r) = 0 taková, že
0+g(r) = 0 taková, že
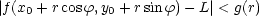

 [0,2p] a r > 0 dostatečně malá.
[0,2p] a r > 0 dostatečně malá.
Speciálně, platí-li po transformaci do polárních souřadnic
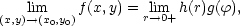
 0+h(r) = 0 a funkce g(
0+h(r) = 0 a funkce g( ) je ohraničená pro
) je ohraničená pro

 [0,2p), pak
[0,2p), pak
Důkaz.
Protože limr 0+g(r) = 0, ke každému
0+g(r) = 0, ke každému  > 0 existuje
> 0 existuje  > 0 tak, že pro
0 < r <
> 0 tak, že pro
0 < r <
 je g(r) <
je g(r) <  , tj.
, tj.

 -okolí
bodu [x0,y0] je
-okolí
bodu [x0,y0] je  f(x,y) − L
f(x,y) − L <
<  , což
je právě definice vztahu
lim(x,y)
, což
je právě definice vztahu
lim(x,y) (x0,y0)f(x,y) = L. □
(x0,y0)f(x,y) = L. □
Příklad 2.4. Rozhodněte, zda existují limity následujících funkcí, a v případě, že ano, vypočítejte je:
i) f(x,y) = 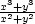 v bodě
[0,0].
v bodě
[0,0].
Řešení. Využijeme transformace do
polárních souřadnic a
tvrzení Věty 2.6
.
Položme x = r cos ,
y =
r sin
,
y =
r sin .
Je-li (x,y)
.
Je-li (x,y)  (0,0), je r
(0,0), je r  0+, a tedy
0+, a tedy
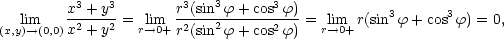
|
 ) = sin3
) = sin3 + cos3
+ cos3 je ohraničená.
je ohraničená.
ii) f(x,y) = 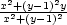 v bodě
[0,1].
v bodě
[0,1].
Řešení. Postupujeme podobně jako v předcházejícím příkladu. Platí
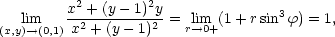
|
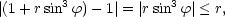
Poznámka 2.3. Podobně jako transformaci do polárních souřadnic při výpočtu limity funkce dvou proměnných používáme při výpočtu limity funkce tří proměnných transformaci do sférických souřadnic

 je úhel, který
svírá průvodič (tj. spojnice
těchto bodů) s kladným směrem osy
z,
a
je úhel, který
svírá průvodič (tj. spojnice
těchto bodů) s kladným směrem osy
z,
a  je úhel, který
svírá průmět průvodiče do
podstavné roviny
je úhel, který
svírá průmět průvodiče do
podstavné roviny  xy s kladným směrem
osy x. Zejména
jestliže po zavedení
sférických souřadnic vyjde výraz
závisející na
xy s kladným směrem
osy x. Zejména
jestliže po zavedení
sférických souřadnic vyjde výraz
závisející na  nebo
nebo
 , limita neexistuje
(toto odpovídá skutečnosti,
že
při
„blížení“ se po
různých přímkách k limitnímu bodu dostaneme
různé hodnoty).
, limita neexistuje
(toto odpovídá skutečnosti,
že
při
„blížení“ se po
různých přímkách k limitnímu bodu dostaneme
různé hodnoty).
V některých speciálních případech je k vyšetřování existence limity vhodná následující věta, která se někdy v literatuře bere za definici limity (tzv. Heineho2 definice). Důkaz této věty neuvádíme, neboť je v podstatě stejný jako pro analogické tvrzení týkající se funkce jedné proměnné, viz [N1], strana 189.
Věta 2.7. Nechť
[x0,y0] je hromadný
bod definičního oboru
 (f) funkce f
:
(f) funkce f
:  2
2 
 . Funkce
f má v tomto
bodě limitu L, právě když pro každou posloupnost bodů
{[xn,yn]}, kde [xn,yn]≠[x0,y0] pro velká n, konvergující k bodu [x0,y0], má posloupnost {f(xn,yn)} limitu
L.
. Funkce
f má v tomto
bodě limitu L, právě když pro každou posloupnost bodů
{[xn,yn]}, kde [xn,yn]≠[x0,y0] pro velká n, konvergující k bodu [x0,y0], má posloupnost {f(xn,yn)} limitu
L.
Pro funkci n proměnných dostáváme zcela stejnou definici spojitosti:
Nechť f je funkce n proměnných, n ≥ 2. Řekneme, že funkce f je spojitá v bodě x∗ = [x1∗,…,xn∗], jestliže má v tomto bodě vlastní limitu a platí
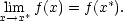
Porovnejme tuto definici
s definicí spojitosti
zobrazení mezi metrickými prostory. Zobrazení f z prostoru
(P, ) do prostoru
(Q,
) do prostoru
(Q, ) je
spojité v bodě
x∗
) je
spojité v bodě
x∗  P,
jestliže ke každému
okolí
P,
jestliže ke každému
okolí 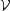 bodu
f(x∗)
bodu
f(x∗)  Q existuje okolí
Q existuje okolí
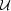 bodu
x∗ takové, že pro
každé x∗
bodu
x∗ takové, že pro
každé x∗

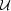 je f(x∗)
je f(x∗) 
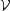 . Je-li
(P,
. Je-li
(P, ) prostor
) prostor
 n
s některou
z výše uvedených
ekvivalentních metrik
n
s některou
z výše uvedených
ekvivalentních metrik  1,
1, 2,
2,
 (viz
odstavec 2.1.) a (Q,
(viz
odstavec 2.1.) a (Q, )
je
)
je  1 s metrikou
1 s metrikou  (x,y) =
(x,y) =  x
− y
x
− y , pak je
definice spojitého zobrazení
stejná s definicí
spojité funkce n
proměnných v bodě
x∗.
, pak je
definice spojitého zobrazení
stejná s definicí
spojité funkce n
proměnných v bodě
x∗.
Vzhledem k tomu, že spojitost funkce dvou a více proměnných se definuje pomocí pojmu limity funkce stejně jako pro funkci jedné proměnné, obdobně platí věta, že součet, součin a podíl spojitých funkcí je spojitá funkce, a dále platí věta o spojitosti složené funkce.
Věta 2.8. Jsou-li funkce f,g spojité v bodě [x0,y0]

 2,
pak jsou v tomto bodě spojité i funkce f +
g, fg, a je-li g(x0,y0)≠0, je
v tomto bodě spojitá také funkce f∕g.
2,
pak jsou v tomto bodě spojité i funkce f +
g, fg, a je-li g(x0,y0)≠0, je
v tomto bodě spojitá také funkce f∕g.
Příkladem funkcí spojitých v celé rovině jsou např. polynomy ve dvou proměnných, funkce sinu,cosu,eu, kde u je polynom ve dvou proměnných.
Příklad 2.5. Určete body, v nichž nejsou následující funkce spojité
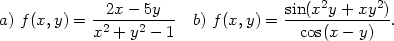
Řešení. a) Funkce f1(x,y) = 2x−5y,f2(x,y) = x2+y2−1 jsou polynomy ve dvou proměnných a ty jsou spojité v celé rovině. Funkce f není spojitá v bodech, ve kterých není definována, tj. kde x2 + y2 = 1. Body, v nichž funkce není spojitá, tvoří kružnici se středem v počátku a s poloměrem 1.
b) Funkce f1(x,y) = x2y + xy2,f2(x,y) = x − y a sinu,cosu jsou spojité v celé rovině. Podle Věty 2.9 o podílu není funkce f spojitá v bodech, kde
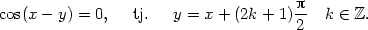
Příklad 2.6. Zjistěte, zda funkce f(x,y) definovaná následujícím způsobem je spojitá v bodě [0,0]:
![{ 3 xx4+yy4 pro [x,y] ⁄= [0,0], f(x,y) = 0 pro [x,y] = [0,0].](diferencialni-pocet168x.png)
Řešení. Nejprve
ověřme, zda existuje lim(x,y) (0,0)f(x,y).
Zvolíme-li y = kx,
snadno vidíme, že výsledná hodnota záleží na k, neboli že záleží na přímce, po které se
k počátku blížíme. Proto uvedená limita neexistuje a daná
funkce nemůže být v počátku spojitá.
(0,0)f(x,y).
Zvolíme-li y = kx,
snadno vidíme, že výsledná hodnota záleží na k, neboli že záleží na přímce, po které se
k počátku blížíme. Proto uvedená limita neexistuje a daná
funkce nemůže být v počátku spojitá.
Poznámka 2.4. Je-li
funkce f spojitá
v bodě
[x0,y0] 
 2, pak
jsou spojité i funkce
jedné proměnné g(x) = f(x,y0) v bodě
x0 a
h(y) = f(x0,y) v bodě
y0.
Spojitá funkce dvou proměnných je tedy spojitou funkcí proměnné x
při
konstantním y
a spojitou funkcí
y při
konstantním x. Opačné tvrzení
neplatí! Ze spojitosti
vzhledem k jednotlivým
proměnným neplyne spojitost jakožto funkce dvou
proměnných.
2, pak
jsou spojité i funkce
jedné proměnné g(x) = f(x,y0) v bodě
x0 a
h(y) = f(x0,y) v bodě
y0.
Spojitá funkce dvou proměnných je tedy spojitou funkcí proměnné x
při
konstantním y
a spojitou funkcí
y při
konstantním x. Opačné tvrzení
neplatí! Ze spojitosti
vzhledem k jednotlivým
proměnným neplyne spojitost jakožto funkce dvou
proměnných.
Uvažujme funkci
z předchozího příkladu.
Není obtížné ověřit, že pro libovolná
pevná
x0,y0

 jsou
funkce f(x,y0),f(x0,y) spojité v
jsou
funkce f(x,y0),f(x0,y) spojité v  , avšak funkce dvou proměnných f není spojitá
v bodě
[0,0], neboť
v tomto
bodě limita neexistuje.
, avšak funkce dvou proměnných f není spojitá
v bodě
[0,0], neboť
v tomto
bodě limita neexistuje.
Stejně jako pro funkci jedné proměnné platí pro funkci n proměnných Weierstrassova3 a Bolzanova4 věta. Uvedeme obě věty pro funkci dvou proměnných.
Připomeňme, že Weierstrassova věta pro funkce jedné proměnné se týká funkcí spojitých na uzavřeném a ohraničeném intervalu, přičemž spojitost na uzavřeném intervalu znamená spojitost zleva (zprava) v pravém (levém) krajním bodě a normální spojitost ve vnitřních bodech. Pro funkci dvou proměnných definujeme spojitost na množině takto:
|
Definice 2.4. Řekneme, že funkce
f je spojitá
na množině M
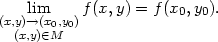
|
Limitní vztah chápeme takto: Ke každému
 > 0 existuje
> 0 existuje  > 0
takové, že pro každé [x,y]
> 0
takové, že pro každé [x,y]


 ([x0,y0])
([x0,y0])
 M platí
M platí  f(x,y)
− f(x0,y0)
f(x,y)
− f(x0,y0) <
<  .
.
Důkaz. Uvedená věta je důsledkem obecné věty z metrických prostorů: Je-li f spojité zobrazení mezi metrickými prostory, pak obrazem kompaktní množiny je kompaktní množina. V Euklidovských prostorech je kompaktní množinou každá ohraničená uzavřená množina. Odtud okamžitě plyne ohraničenost množiny f(M). Protože každá neprázdná shora ohraničená množina má supremum, existuje
 M takový, že f(x0,y0) =
K. Podle definice suprema
existuje pro libovolné n
M takový, že f(x0,y0) =
K. Podle definice suprema
existuje pro libovolné n

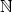 bod [xn,yn]
bod [xn,yn]
 M tak, že f(xn,yn)
> K −
M tak, že f(xn,yn)
> K − . Posloupnost {[xn,yn]} je
ohraničená, proto existuje vybraná podposloupnost {[xnk,ynk]}
konvergující k bodu [x0,y0].
Vzhledem k uzavřenosti množiny M je [x0,y0]
. Posloupnost {[xn,yn]} je
ohraničená, proto existuje vybraná podposloupnost {[xnk,ynk]}
konvergující k bodu [x0,y0].
Vzhledem k uzavřenosti množiny M je [x0,y0]
 M a ze spojitosti funkce f plyne, že {f(xnk,ynk)}
M a ze spojitosti funkce f plyne, že {f(xnk,ynk)} f(x0,y0).
Poněvadž f(xnk,ynk) > K
−
f(x0,y0).
Poněvadž f(xnk,ynk) > K
−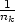 pro všechna k, je
limk
pro všechna k, je
limk
 f(xnk,ynk) = f(x0,y0)
≥ K. Z definice suprema plyne
f(x0,y0)
≤ K, a proto f(x0,y0) =
K.
f(xnk,ynk) = f(x0,y0)
≥ K. Z definice suprema plyne
f(x0,y0)
≤ K, a proto f(x0,y0) =
K.
Podobně se dokáže tvrzení o nejmenší hodnotě funkce f. □
Poznámka 2.5. Důsledkem této věty je ohraničenost spojité funkce na kompaktní množině, což bývá někdy spolu s Větou 2.10 formulováno ve dvou větách jako první a druhá Weierstrassova věta.
V následující větě je
třeba
předpokládat,
že
množina M je souvislá. Připomeňme z teorie metrických
prostorů, že otevřená množina M 
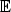 2 se
nazývá souvislá,
jestliže pro každé dva body
X,Y
2 se
nazývá souvislá,
jestliže pro každé dva body
X,Y  M existuje
konečná posloupnost bodu X1,…,Xn
M existuje
konečná posloupnost bodu X1,…,Xn  M, X1
= X,Xn
= Y
taková, že všechny
úsečky XiXi+1 jsou
podmnožinami M.
M, X1
= X,Xn
= Y
taková, že všechny
úsečky XiXi+1 jsou
podmnožinami M.
Věta 2.11. (Bolzanova) Nechť funkce f je spojitá na otevřené souvislé množině
M 
 2.
Nechť pro A,B
2.
Nechť pro A,B  M
platí f(A)≠f(B). Pak
ke každému číslu c ležícímu
mezi hodnotami f(A) a
f(B)
existuje C
M
platí f(A)≠f(B). Pak
ke každému číslu c ležícímu
mezi hodnotami f(A) a
f(B)
existuje C  M tak,
že f(C) =
c.
M tak,
že f(C) =
c.
Důkaz. Položme
g(x,y) =
f(x,y)
−c. Ze souvislosti množiny M plyne existence konečné posloupnosti bodů
X1,…,Xn
 M, X1
= X,Xn
= Y takové, že všechny úsečky XiXi+1 jsou
podmnožinami M. Uvažujeme-li
hodnoty g(Xi), pak
buď existuje index i takový, že
g(Xi) = 0,
nebo existuje j takové, že
g(Xj)
< 0 (>
0), g(Xj+1) >
0 (<
0). Označíme-li Xj
= [x1,y1],
Xj+1 = [x2,y2], jsou
parametrické rovnice úsečky XjXj+1
M, X1
= X,Xn
= Y takové, že všechny úsečky XiXi+1 jsou
podmnožinami M. Uvažujeme-li
hodnoty g(Xi), pak
buď existuje index i takový, že
g(Xi) = 0,
nebo existuje j takové, že
g(Xj)
< 0 (>
0), g(Xj+1) >
0 (<
0). Označíme-li Xj
= [x1,y1],
Xj+1 = [x2,y2], jsou
parametrické rovnice úsečky XjXj+1
![x = x + (x − x )t, y = y + (y − y )t, t ∈ [0,1]. 1 2 1 1 2 1](diferencialni-pocet173x.png)
 [0,1]. Pak
G(0) = g(Xj)
< 0 (>
0), G(1) =
g(Xj+1) >
0 (<
0) a G je spojitá funkce na uzavřeném intervalu.
Podle Bolzanovy věty pro funkci jedné proměnné existuje
t0
[0,1]. Pak
G(0) = g(Xj)
< 0 (>
0), G(1) =
g(Xj+1) >
0 (<
0) a G je spojitá funkce na uzavřeném intervalu.
Podle Bolzanovy věty pro funkci jedné proměnné existuje
t0  (0,1) tak,
že G(t0) = 0.
Zvolíme-li C = [x1
+ (x2
− x1)t0,y1
+ (y2
− y1)t0],
dostaneme g(C) = 0,
tj. f(C) =
c. □
(0,1) tak,
že G(t0) = 0.
Zvolíme-li C = [x1
+ (x2
− x1)t0,y1
+ (y2
− y1)t0],
dostaneme g(C) = 0,
tj. f(C) =
c. □
Poznámka 2.6. Důsledkem této věty je
následující tvrzení: Nechť funkce f je spojitá na otevřené souvislé množině
M 
 2.
Existují-li A,B
2.
Existují-li A,B  M
takové, že f(A)
< 0,f(B)
> 0, pak existuje C
M
takové, že f(A)
< 0,f(B)
> 0, pak existuje C  M tak, že f(C) = 0
(tzv. první Bolzanova věta).
M tak, že f(C) = 0
(tzv. první Bolzanova věta).
Cvičení 
2.1. Pomocí konkrétní specifikace okolí limitního bodu a limity definujte:
a) lim(x,y) (−1,2)f(x,y) = (−1,2)f(x,y) =
 |
b) lim(x,y) ( ( ,1)f(x,y) =
− ,1)f(x,y) =
− |
2.2. Vypočtěte limity následujících funkcí:
a) lim(x,y) (1,1) (1,1)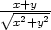 |
d) lim(x,y) (−4,−1) (−4,−1)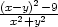 |
b) lim(x,y) (e2,1) (e2,1)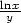 |
e) lim(x,y) (0,0)xy2
cos (0,0)xy2
cos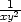 |
c) lim(x,y) (1,0) (1,0) |
2.3. Vypočtěte limity následujících funkcí:
a) lim(x,y) (0,0) (0,0)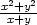 |
e) lim(x,y) ( ( , , ) )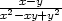 |
b) lim(x,y) (0,0) (0,0)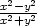 |
f) lim(x,y) (0,2) (0,2)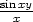 |
c) lim(x,y) (0,0) (0,0)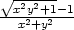 |
g) lim(x,y) ( ( , , ) )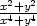 |
d) lim(x,y) (0,0)(x2
+ y2)x2y2 (0,0)(x2
+ y2)x2y2 |
h) lim(x,y) (0,2) (0,2)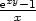 |
2.4. Vypočtěte limity následujících funkcí:
a) lim(x,y) ( ( , , )(x2
+ y2)e−(x+y) )(x2
+ y2)e−(x+y) |
d) lim(x,y) ( ( , , ) ) 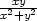  x2 x2 |
b) lim(x,y) ( ( ,1) ,1)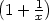 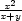 |
e) lim(x,y) (0,0) (0,0)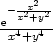 |
c) lim(x,y) (0,0) (0,0) |
f) lim(x,y) (0,0)(1 +
x2y2)− (0,0)(1 +
x2y2)−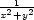 |
∗
Učitel by měl působit tak, že to, co nabídne, je přijímáno jako cenný dar, ne jako úmorná povinnost. (A. Einstein)
∗
1Guillaume de l’Hospital (1661–1704), francouzský matematik
2Heinrich Heine (1821–1881), německý matematik
3Karl T. W. Weierstrass (1815–1897), německý matematik
4Bernard Bolzano (1781–1848), český matematik a filozof
[Další] [Předchozí] [Předchozí – na konec] [Na začátek] [Výše]