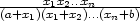Příklad 6.6. i) Určete nejmenší a největší hodnotu funkce
z = f(x,y) =
xy − x2
− y2
+ x +
y v trojúhelníku tvořeném
souřadnými osami a tečnou ke grafu funkce y =
 v bodě [2,2].
v bodě [2,2].
Řešení. Nejprve určeme rovnici tečny ke grafu funkce
y = 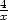 . Platí y
. Platí y = −
= −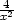 , tj. rovnice tečny
je y−2 =
−
, tj. rovnice tečny
je y−2 =
−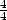 (x−2) =
−x+2.
Tedy množinou M, na níž hledáme
absolutní extrémy, je množina
(x−2) =
−x+2.
Tedy množinou M, na níž hledáme
absolutní extrémy, je množina
![M = {[x, y] ∈ ℝ2 : x ≥ 0,y ≥ 0,y ≤ 4 − x}.](diferencialni-pocet666x.png)
Určíme stacionární body funkce
z

odkud dostáváme stacionární bod
[x,y] =
[1,1]  M
M.
Nyní vyšetřeme funkci f na hranici množiny M, která se skládá z úseček
I. y
= 0, x  [0,4] II.
x =
0, y
[0,4] II.
x =
0, y  [0,4] III.
y =
4 − x, x
[0,4] III.
y =
4 − x, x
 [0,4].
[0,4].
I. y
= 0, x  [0,4].
Dosazením dostáváme u
= f(x,0) =
−x2
+ x a hledáme absolutní extrémy této funkce
jedné proměnné pro x
[0,4].
Dosazením dostáváme u
= f(x,0) =
−x2
+ x a hledáme absolutní extrémy této funkce
jedné proměnné pro x
 [0,4].
Platí u
[0,4].
Platí u (x) =
−2x
+ 1 = 0, odtud x =
(x) =
−2x
+ 1 = 0, odtud x =
 . Funkční hodnoty ve stacionárním bodě a v krajních
bodech intervalu jsou u(
. Funkční hodnoty ve stacionárním bodě a v krajních
bodech intervalu jsou u( )
=
)
=  , u(0) =
0, u(4) = 12.
, u(0) =
0, u(4) = 12.
II. x
= 0, y  [0,4].
Dosazením dostáváme v
= f(0,y) =
−y2
+ y a stejně jako v části
I v(0) = 0, v(4) =
−12, v(
[0,4].
Dosazením dostáváme v
= f(0,y) =
−y2
+ y a stejně jako v části
I v(0) = 0, v(4) =
−12, v( )
=
)
=  .
.
III. y
= 4 − x, x  [0,4].
Dosazením dostáváme w
= f(x,4
− x) =
x(4 −
x) −
x2 −
(4 − y)2
+ x + 4
− x =
−3x2
+ 12x −
12. Platí w
[0,4].
Dosazením dostáváme w
= f(x,4
− x) =
x(4 −
x) −
x2 −
(4 − y)2
+ x + 4
− x =
−3x2
+ 12x −
12. Platí w (x) =
−6x
+ 12 = 0, odtud x = 2,
w(2) = 0.
V krajních bodech w(0) =
−12,w(4) =
−12.
(x) =
−6x
+ 12 = 0, odtud x = 2,
w(2) = 0.
V krajních bodech w(0) =
−12,w(4) =
−12.
Porovnáním funkčních hodnot
funkce f na hranici (tj.
hodnot funkcí u,v,w
v jejich stacionárních bodech a v krajních bodech
intervalů, kde tyto funkce vyšetřujeme) s funkční hodnotou
funkce f v jediném
stacionárním bodě [1,1]
vidíme, že
|
fmin
= −12 pro
[x,y] =
[0,4] a [x,y] =
[4,0], |
|
|
|
fmax
= 1 pro [x,y] =
[1,1]. |
|
|
Závěrem poznamenejme, že algebraické úpravy
spojené s vyjádřením funkce f na hranici bývají nejčastějším zdrojem
numerických chyb. Máme však k dispozici poměrně dobrou
průběžnou kontrolu. V bodě [x,y] =
[4,0] se stýkají části hranice I a III, a
tedy funkce u z I musí pro
x =
4 nabývat stejné funkční hodnoty jako funkce w z III v x = 4.
V našem případě je u(4) =
−12
= w(4). Podobně v bodě [0,0] se
stýkají části I a II a v bodě [0,4]
části II a III. Také v těchto bodech průběžná kontrola
vychází, neboť u(0) = 0 = v(0) a
w(0) = v(4) =
−12. Doporučujeme čtenáři tuto kontrolu vždy
provést, neboť značně minimalizuje možnost šíření numerické chyby
ve výpočtu.
ii) Určete nejmenší a největší hodnotu funkce
z =
(2x2 +
3y2)e−x2−y2 na množině
M = {[x,y]

 2
: x2
+ y2
≤ 4}.
2
: x2
+ y2
≤ 4}.
Řešení. Nejprve určíme stacionární body ležící uvnitř
množiny M, kterou je kruh
o poloměru 2.
Vypočteme parciální derivace
| zx
= |
4xe−x2−y2
− 2x(2x2
+ 3y2)e−x2−y2
= −2xe−x2−y2 ![[ 2 2 ] 2x + 3y − 2](diferencialni-pocet673x.png) , , |
|
|
| zy
= |
6ye−x2−y2
− 2y(2x2
+ 3y2)e−x2−y2
= −2ye−x2−y2 ![[ ] 2x2 + 3y2 − 3](diferencialni-pocet674x.png) |
|
|
a položíme je rovny nule:
xe−x2−y2 ![[ 2 2 ] 2x + 3y − 2](diferencialni-pocet675x.png) |
=
0, |
|
|
ye−x2−y2 ![[ ] 2x2 + 3y2 − 3](diferencialni-pocet676x.png) |
=
0. |
|
|
Odtud dostáváme 4 možnosti:
A)
x = 0 = y
⇒ f(0,0) =
0.
B)
x = 0, 3y2
= 3 ⇒ y
=  1,
f(0,
1,
f(0, 1) = 3e−1
1) = 3e−1.
C)
y = 0, 2x2
= 2 ⇒ x
=  1
1,
f( 1,0) =
2e−1
1,0) =
2e−1.
D)
2x2
+ 3y2
− 2
= 0 a
2x2
+ 3y2
− 3
= 0 – tento systém nemá řešení.
Nyní vyšetřeme funkci f na hranici množiny M. Tu si rozdělíme na dvě části, horní a
dolní půlkružnici.
I. y =  , x
, x  [−2,2],
u = f(x,
[−2,2],
u = f(x,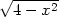 ) =
(2x2 +3(4−x2))e−4 = (12−x2)e−4. Najdeme
největší a nejmenší hodnotu funkce u na intervalu [−2,2].
Těchto extremálních hodnot je dosaženo buď v lokálním extrému
uvnitř intervalu [−2,2],
nebo v některém z krajních bodů x =
) =
(2x2 +3(4−x2))e−4 = (12−x2)e−4. Najdeme
největší a nejmenší hodnotu funkce u na intervalu [−2,2].
Těchto extremálních hodnot je dosaženo buď v lokálním extrému
uvnitř intervalu [−2,2],
nebo v některém z krajních bodů x =
 2. Platí
u
2. Platí
u =
−2xe−4 = 0 ⇒
x =
0. Odtud u(0) = e−4, u(
=
−2xe−4 = 0 ⇒
x =
0. Odtud u(0) = e−4, u( 2) = 8e−4.
2) = 8e−4.
II. y = −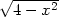 , x
, x  [−2,2]. Zde
je situace zcela stejná jako pro I, neboť f(x,−y) =
f(x,y).
[−2,2]. Zde
je situace zcela stejná jako pro I, neboť f(x,−y) =
f(x,y).
Porovnáním všech vypočtených hodnot vidíme,
že
|
fmax
= 3e−1,
pro [x,y] =
[0, 1], 1], |
|
|
|
fmin
= 0, pro [x,y] =
[0,0]. |
|
|
Graf vyšetřované funkce je znázorněn na obr.
14.13
a
14.14
; zde lze ověřit, že všechny
stacionární body leží uvnitř kruhu
M.
iii) Je dán drát délky l, tento drát je rozdělen na tři části.
Z jedné je vytvořen kruh, z druhé čtverec a ze zbylé
rovnostranný trojúhelník. Určete délky jednotlivých částí tak, aby
plocha omezená těmito obrazci byla minimální, resp. maximální.
Řešení. Označíme-li
x délku strany čtverce,
y poloměr kruhu a z délku strany trojúhelníka, platí
4x +
2py +
3z = l,
odtud z =  . Pro součet obsahů
čtverce, kruhu a trojúhelníka platí
. Pro součet obsahů
čtverce, kruhu a trojúhelníka platí
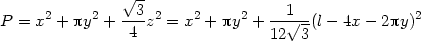
a hledáme absolutní extrémy této funkce na množině
M =
{[x,y] :
x,y ≥ 0, 4x
+ 2py
≤ l}.
Nejprve vypočteme parciální derivace a stacionární body:
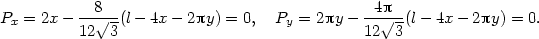
Odtud
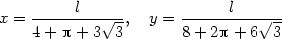
a funkční hodnota v tomto stacionárním bodě je
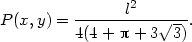
Nyní vyšetřeme funkci P na hranici množiny M.
I. y
= 0,x  [0,
[0,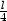 ], označme
], označme 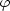 (x) =
P(x,0) =
x2 +
(x) =
P(x,0) =
x2 +
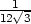 (l −
4x)2.
Pak
(l −
4x)2.
Pak 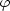 (0)
=
(0)
= 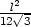 ,
, 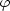 (
(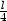 )
=
)
= 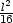 ,
, 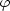
 (x) =
2x −
(x) =
2x −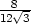 (l
− 4x) = 0,
tj. x=
(l
− 4x) = 0,
tj. x=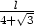 ,
, 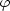 (x) =
(x) =
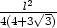 .
.
II. x
= 0,y  [0,
[0,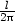 ], označme
], označme 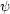 (y) =
P(0,y) =
py2
+
(y) =
P(0,y) =
py2
+ 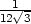 (l −
2py)2.
Platí
(l −
2py)2.
Platí 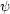 (0)
=
(0)
= 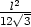 ,
, 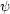 (
(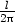 )
=
)
= 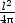 ,
, 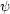
 (y) =
2py −
(y) =
2py −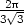 (l
− 2py) =
0 ⇒ y
=
(l
− 2py) =
0 ⇒ y
= 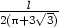 ,
,  (y) =
(y) =
 .
.
III. y
= 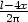 , x
, x  [0,
[0,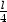 ], označme
], označme  (x) =
P(x,
(x) =
P(x,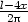 ) = x2
+
) = x2
+  (l −
4x)2.
(l −
4x)2.
 (0)
=
(0)
= 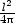 ,
,  (
(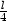 )
=
)
= 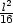 ,
, 
 (x) =
2x −
(x) =
2x − (l
− 4x) =
0 ⇒ x
=
(l
− 4x) =
0 ⇒ x
= 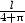 ,
,  (x) =
(x) =
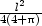 .
.
Porovnáním všech vypočtených hodnot zjistíme, že
největší obsah dostaneme, jestliže celý drát stočíme do kružnice,
tj.
![2 [ ] Pmax = -l- pro [x,y] = 0,-l- , 4p 2p](diferencialni-pocet711x.png)
a nejmenší obsah
Pmin
= P(x,y) =
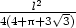
, jestliže jej rozdělíme takto:
| část na čtverec… |
4x
= 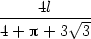 , , |
|
|
| část na kruh… |
2py
= 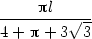 , , |
|
|
| část na trojúhelník… |
3z
= 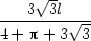 . . |
|
|
 n
n

 nabývá v bodě x∗
nabývá v bodě x∗

 n
lokálního maxima
(minima), jestliže existuje okolí
n
lokálního maxima
(minima), jestliže existuje okolí  (x∗) bodu
x∗ takové, že pro každé x
(x∗) bodu
x∗ takové, že pro každé x 
 (x∗) platí
f(x)
≤ f(x∗)
(f(x)
≥ f(x∗)).
(x∗) platí
f(x)
≤ f(x∗)
(f(x)
≥ f(x∗)). má v bodě
má v bodě ![{ 2 2 f(x,y) = x + y , pro [x,y] ⁄= [0,0], 1, pro [x,y] = [0,0],](diferencialni-pocet612x.png)
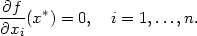

![D(x0, y0) = fxx(x0,y0)fyy(x0,y0)− [fxy(x0,y0)]2 > 0,](diferencialni-pocet616x.png)
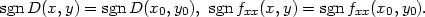
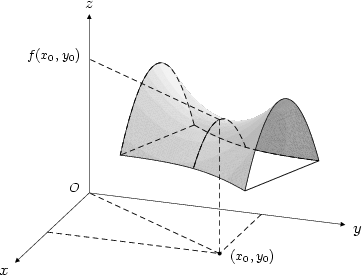
![1 f(x,y) = f (x0,y0) +-[fxx(c1,c2)(x− x0)2+ 2 2 +2fxy(c1,c2)(x − x0)(y − y0)+ fyy(c1,c2)(y − y0)]](diferencialni-pocet618x.png)
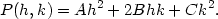
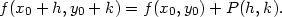
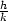
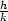
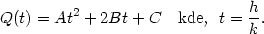
 t
t

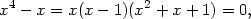
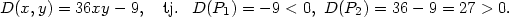

![D(x,y) = f f − [f ]2 = (12x2 − 2)(12y2 − 2)− 4. xx yy xy](diferencialni-pocet629x.png)

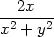
![[ 2 2 2x2 ] ln(x + y )+ x2 +-y2](diferencialni-pocet631x.png)
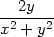
![[ ] ln(x2 + y2)+ --2y2-- x2 + y2](diferencialni-pocet633x.png)

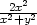
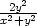
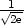
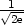
![[ ] √1-,√1-- 2e 2e](diferencialni-pocet638x.png) (ležícím uvnitř jednotkové kružnice) je lokální
minimum, neboť na hranici množiny, která je tvořena souřadnými
osami a jednotkovou kružnicí a kde leží tento bod, je funkce
nulová a uvnitř této množiny je funkce
(ležícím uvnitř jednotkové kružnice) je lokální
minimum, neboť na hranici množiny, která je tvořena souřadnými
osami a jednotkovou kružnicí a kde leží tento bod, je funkce
nulová a uvnitř této množiny je funkce ![[ --1 -1-] −√2e-,−√2e-](diferencialni-pocet639x.png) a ve zbývajících dvou bodech je
lokální maximum. Graf funkce
a ve zbývajících dvou bodech je
lokální maximum. Graf funkce 


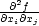
 >
>

 >
>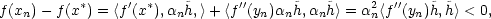
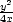
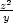

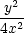
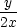
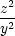
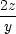
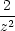
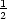

 v bodě
v bodě 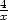 . Platí
. Platí 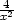 , tj. rovnice tečny
je
, tj. rovnice tečny
je 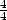
![M = {[x, y] ∈ ℝ2 : x ≥ 0,y ≥ 0,y ≤ 4 − x}.](diferencialni-pocet666x.png)

 . Funkční hodnoty ve stacionárním bodě a v krajních
bodech intervalu jsou
. Funkční hodnoty ve stacionárním bodě a v krajních
bodech intervalu jsou 
 ,
, 
 .
.![[ 2 2 ] 2x + 3y − 2](diferencialni-pocet673x.png)
![[ ] 2x2 + 3y2 − 3](diferencialni-pocet674x.png)
![[ 2 2 ] 2x + 3y − 2](diferencialni-pocet675x.png)
![[ ] 2x2 + 3y2 − 3](diferencialni-pocet676x.png)

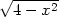
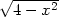
 . Pro součet obsahů
čtverce, kruhu a trojúhelníka platí
. Pro součet obsahů
čtverce, kruhu a trojúhelníka platí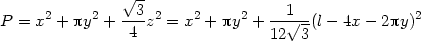
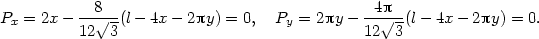
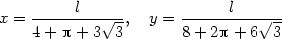
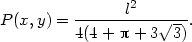
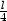
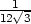
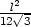 ,
, 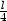
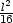 ,
, 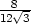
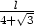 ,
, 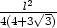
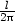
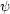
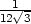
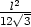 ,
, 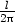
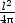 ,
, 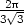
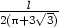 ,
, 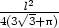 .
.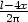
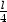

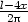

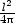 ,
, 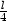
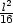 ,
, 
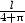 ,
, 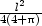 .
.![2 [ ] Pmax = -l- pro [x,y] = 0,-l- , 4p 2p](diferencialni-pocet711x.png)
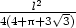 , jestliže jej rozdělíme takto:
, jestliže jej rozdělíme takto:
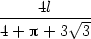
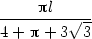
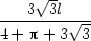
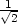 . Minimum nastává v bodě
. Minimum nastává v bodě
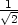
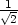
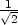
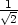
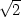 ,
, 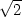 . Všimněme
si také, že průsečíky přímky
. Všimněme
si také, že průsečíky přímky 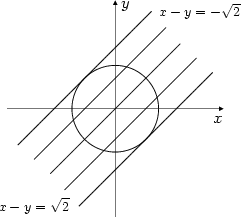

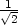
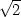 , a minimum
je v bodě
, a minimum
je v bodě 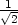
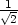
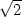 .
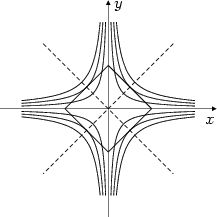
. ). Stejnou úvahou jako v předchozím příkladu
zjistíme, že funkce nabývá absolutního maxima
). Stejnou úvahou jako v předchozím příkladu
zjistíme, že funkce nabývá absolutního maxima  v bodech
v bodech 

 v bodech
v bodech 



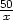
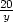
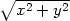
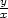

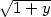
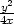
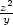
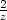 ,
, 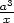
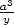



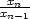
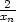 ,
,