![M = {[x,y] ∈ 𝒟(F ) : F (x,y) = 0}.](diferencialni-pocet825x.png)
[Další] [Předchozí] [Předchozí – na konec] [Na konec] [Výše]
Uvažujme tento problém: Nechť F je funkce dvou proměnných a označme množinu (křivku)
![M = {[x,y] ∈ 𝒟(F ) : F (x,y) = 0}.](diferencialni-pocet825x.png)
Zvolme libovolný bod na křivce M. Chceme vyšetřit chování křivky v okolí tohoto bodu, zejména určit rovnici tečny v tomto bodě a rozhodnout, zda křivka v okolí tohoto bodu leží nad, nebo pod tečnou.
Jestliže křivka M je přímo grafem funkce jedné proměnné
y = f(x),
tj. F(x,y) =
y − f(x) = 0,
problém snadno vyřešíme výpočtem derivací f ,f
,f
 . Rovněž
v jednoduchých případech, jako je rovnice kružnice, lze využít
metod diferenciálního počtu funkcí jedné proměnné, neboť
z rovnice kružnice můžeme snadno spočítat y jako funkci proměnné x. Je-li však rovnice křivky
komplikovanější, např. x3
+ y3
− 2xy
= 0, a chceme určit rovnici
tečny ke křivce určené touto rovnicí v bodě [x0,y0] =
[1,1], předchozí postup selhává, protože
z rovnice křivky nelze y
rozumně spočítat.
. Rovněž
v jednoduchých případech, jako je rovnice kružnice, lze využít
metod diferenciálního počtu funkcí jedné proměnné, neboť
z rovnice kružnice můžeme snadno spočítat y jako funkci proměnné x. Je-li však rovnice křivky
komplikovanější, např. x3
+ y3
− 2xy
= 0, a chceme určit rovnici
tečny ke křivce určené touto rovnicí v bodě [x0,y0] =
[1,1], předchozí postup selhává, protože
z rovnice křivky nelze y
rozumně spočítat.
V této kapitole ukážeme, jak tuto nesnáz obejít. Budeme se nejprve zabývat problémem, zda je křivka M v okolí daného bodu totožná s grafem nějaké funkce jedné proměnné, a pokud ano, jak spočítat její derivace.
V prvním odstavci je tento problém vyřešen pro funkci jedné proměnné, v druhém pro funkci n proměnných a v třetím odstavci pro zobrazení mezi prostory vyšších dimenzí.
Jinými slovy, funkce y =
f(x) je
v okolí bodu [x0,y0] zadána
implicitně1 rovnicí F(x,y) =
0, jestliže existuje  >
0 takové, že F(x,f(x)) = 0
pro x
>
0 takové, že F(x,f(x)) = 0
pro x  (x0
−
(x0
−  ,x0
+
,x0
+  ).
).
V případě rovnice kružnice x2
+ y2
− 1
= 0 z obrázku vidíme, že v okolí libovolného bodu
P0≠[ 1,0] této
kružnice je rovnicí x2
+ y2
− 1
= 0 implicitně zadána funkce y =
f(x) =
1,0] této
kružnice je rovnicí x2
+ y2
− 1
= 0 implicitně zadána funkce y =
f(x) =

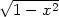 (znaménko + bereme, leží-li bod na horní
půlkružnici, a znaménko −,
je-li na dolní půlkružnici).
(znaménko + bereme, leží-li bod na horní
půlkružnici, a znaménko −,
je-li na dolní půlkružnici).
Dále vidíme, že v okolí bodů [ 1,0] není
rovnicí zadána žádná funkce proměnné x.
1,0] není
rovnicí zadána žádná funkce proměnné x.
Jako jiný příklad uvažujme křivky dané rovnicemi
| F(x,y) := x − y2 = 0 | (parabola) |
| F(x,y) := x2 − y2 = 0 | (dvojice přimek y =
 x) x) |
Je vidět, že v libovolném okolí počátku
není rovnicí F(x,y) = 0
určena implicitně žádná funkce. Naopak v dostatečně malém
okolí každého jiného bodu těchto křivek je rovnicí F(x,y) = 0
definována funkce y = f(x).
V prvním případě to jsou funkce y =
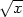 nebo y = −
nebo y = −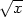 , podle toho, leží-li bod v horní,
nebo dolní polorovině určené osou x, ve druhém případě y =
x nebo y =
−x, podle toho, na které z dvojice
přímek bod leží.
, podle toho, leží-li bod v horní,
nebo dolní polorovině určené osou x, ve druhém případě y =
x nebo y =
−x, podle toho, na které z dvojice
přímek bod leží.
V následující Větě 8.1 je uvedena postačující podmínka pro existenci funkce zadané implicitně v okolí daného bodu křivky a ve Větě 8.2 způsob pro výpočet její derivace.
Věta 8.1. Nechť je funkce F
spojitá na čtverci R
= {[x,y]

 (F):
(F): x −
x0
x −
x0 < a,
< a,  y
− y0
y
− y0 < a}
a nechť F(x0,y0) = 0.
Dále předpokládejme, že funkce F má spojitou parciální derivaci
< a}
a nechť F(x0,y0) = 0.
Dále předpokládejme, že funkce F má spojitou parciální derivaci 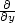 F(x,y)
v bodě [x0,y0] a platí
F(x,y)
v bodě [x0,y0] a platí
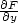 (x0,y0)≠0.
(x0,y0)≠0.
Pak existuje okolí bodu [x0,y0], v němž je rovností F(x,y) = 0 implicitně definována právě jedna funkce y = f(x), která je spojitá.
Důkaz. Existenci
implicitně zadané funkce dokážeme pomocí Banachovy věty
o pevném bodu kontraktivního zobrazení v úplném metrickém
prostoru, viz [D-D]. Nechť
 ,
, > 0
jsou reálná čísla, jejichž přesnou hodnotu určíme později, a
označme I = [x0
−
> 0
jsou reálná čísla, jejichž přesnou hodnotu určíme později, a
označme I = [x0
− ,x0
+
,x0
+  ].
Uvažujme prostor funkcí
].
Uvažujme prostor funkcí
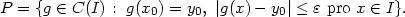
 -
- obdélníku kolem bodu [x0,y0]. Na
P uvažujme metriku stejnoměrné
konvergence
obdélníku kolem bodu [x0,y0]. Na
P uvažujme metriku stejnoměrné
konvergence  (f,g) =
maxx
(f,g) =
maxx I
I f(x)
−g(x)
f(x)
−g(x) . Označme
d = Fy(x0,y0)≠0 a
definujme na P zobrazení
T : P
. Označme
d = Fy(x0,y0)≠0 a
definujme na P zobrazení
T : P
 C(I)
předpisem
C(I)
předpisem
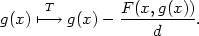
 P zobrazení T, je tento bod hledanou implicitně zadanou
funkcí f. Vskutku, je-li
f(x) =
T(f)(x) =
f(x)
− d−1F(x,f(x)), je
d−1F(x,f(x)) = 0
pro x
P zobrazení T, je tento bod hledanou implicitně zadanou
funkcí f. Vskutku, je-li
f(x) =
T(f)(x) =
f(x)
− d−1F(x,f(x)), je
d−1F(x,f(x)) = 0
pro x  I, což
podle Definice 8.1
znamená, že funkce f je implicitně zadána rovností
F(x,y) =
0.
I, což
podle Definice 8.1
znamená, že funkce f je implicitně zadána rovností
F(x,y) =
0.
Určíme nyní konstanty  a
a  tak, aby
zobrazení T bylo kontrakcí a
zobrazovalo prostor P do sebe
(což jsou spolu s úplností prostoru P předpoklady Banachovy věty).
tak, aby
zobrazení T bylo kontrakcí a
zobrazovalo prostor P do sebe
(což jsou spolu s úplností prostoru P předpoklady Banachovy věty).
Nechť f,g
 P. Využitím Lagrangeovy věty o střední
hodnotě pro funkci F
dostáváme
P. Využitím Lagrangeovy věty o střední
hodnotě pro funkci F
dostáváme
 T(f)(x)−T(g)(x) T(f)(x)−T(g)(x) = maxx = maxx I I f(x)−d−1F(x,f(x))
− g(x) +
d−1F(x,g(x)) f(x)−d−1F(x,f(x))
− g(x) +
d−1F(x,g(x)) = = |
|||
=
 f(x)
− g(x)
− f(x)
− g(x)
−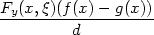  = =  f(x)
− g(x) f(x)
− g(x)  1 − 1 −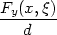  , , |
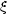 =
=
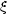 (x) leží
mezi f(x) a
g(x).
Protože funkce Fy
je spojitá v bodě [x0,y0] a
Fy(x0,y0) =
d, existují
(x) leží
mezi f(x) a
g(x).
Protože funkce Fy
je spojitá v bodě [x0,y0] a
Fy(x0,y0) =
d, existují  ,
, 1
> 0 taková, že
1
> 0 taková, že  1
− d−1Fy(x,y)
1
− d−1Fy(x,y) <
< 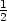 pro x
pro x  (x0
−
(x0
−  1,x0
+
1,x0
+  1),
y
1),
y  (y0
−
(y0
−  ,y0
+
,y0
+  ). Je-li
). Je-li
 ≤
≤
 1, pro
takto zvolená
1, pro
takto zvolená  ,
, 1 platí
1 platí
 (T(f),T(g)) (T(f),T(g)) |
=
maxx I I f(x)
− g(x) f(x)
− g(x)  1 − 1 −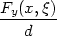  ≤ ≤ |
||
≤ maxx maxx I I f(x)
− g(x) f(x)
− g(x) = =   (f,g), (f,g), |
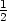 . Nechť f
. Nechť f
 P. Pak T(f) je
spojitá funkce a T(f)(x0) =
f(x0)
− d−1F(x0,f(x0)) =
y0. Odtud plyne existence
P. Pak T(f) je
spojitá funkce a T(f)(x0) =
f(x0)
− d−1F(x0,f(x0)) =
y0. Odtud plyne existence  2
> 0 tak, že pro x
2
> 0 tak, že pro x  (x0
−
(x0
−  2,x0
+
2,x0
+  2) platí
2) platí

Položme  = min{
= min{ 1,
1, 2}, pak
pro takto určená
2}, pak
pro takto určená  ,
, je
T kontraktivní
zobrazení P do sebe, což
jsme potřebovali dokázat. □
je
T kontraktivní
zobrazení P do sebe, což
jsme potřebovali dokázat. □
Poznámka 8.1. i) Uvědomme si, že rovností F(x,y) = 0 může být v dostatečně velkém okolí bodu [x0,y0] zadána jedna či více spojitých nebo nespojitých funkcí. Tuto skutečnost ilustruje následující příklad.
Uvažujme rovnici y(y
− 1) = 0. Touto rovnicí je v okolí bodu
[0,0]
určena spojitá funkce y
 0
a kromě ní také nespojitá funkce
0
a kromě ní také nespojitá funkce
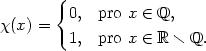
 y=0 = 0, a přesto je rovnicí v okolí
počátku implicitně určena funkce y =
y=0 = 0, a přesto je rovnicí v okolí
počátku implicitně určena funkce y =
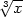 .
.
iii) Na zadávající rovnici F(x,y) = 0
se můžeme dívat také jako na rovnici definující funkci x =
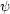 (y)
proměnné y. Snadno se vidí
na základě Věty 8.1
, že dostatečnou podmínkou pro
existenci takto implicitně zadané funkce x =
(y)
proměnné y. Snadno se vidí
na základě Věty 8.1
, že dostatečnou podmínkou pro
existenci takto implicitně zadané funkce x =
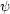 (y)
v okolí b.
[x0,y0] je
Fx(x0,y0)≠0. Na
obrázku 8.2
je vidět, že rovnicí x2
+ y2
− 1
= 0 je v okolí bodu [1,0]
implicitně určena funkce x
=
(y)
v okolí b.
[x0,y0] je
Fx(x0,y0)≠0. Na
obrázku 8.2
je vidět, že rovnicí x2
+ y2
− 1
= 0 je v okolí bodu [1,0]
implicitně určena funkce x
= 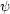 (y) =
(y) =
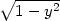 .
.
Derivaci implicitně zadané funkce vypočteme podle následující věty.
Věta 8.2. Nechť jsou splněny předpoklady Věty 8.1 a funkce F má na R spojité parciální derivace 1. řádu. Pak má funkce f, která je implicitně určena v okolí bodu [x0,y0] rovnicí F(x,y) = 0, derivaci v bodě x0 a platí
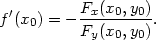 |
(8.1) |
Důkaz. Nechť
f je funkce implicitně určená
v okolí bodu [x0,y0] rovnicí
F(x,y) =
0, tj. existuje  >
0 takové, že pro x
>
0 takové, že pro x  (x0
−
(x0
−  ,x0
+
,x0
+  ) platí
F(x,f(x)) = 0.
Důkaz existence derivace implicitně zadané funkce f zde nebudeme provádět (lze jej
s podrobnostmi nalézt např. v [N
2]), zde se zaměříme pouze na odvození
vzorce pro f
) platí
F(x,f(x)) = 0.
Důkaz existence derivace implicitně zadané funkce f zde nebudeme provádět (lze jej
s podrobnostmi nalézt např. v [N
2]), zde se zaměříme pouze na odvození
vzorce pro f . Derivováním rovnosti F(x,f(x))
podle x dostáváme
. Derivováním rovnosti F(x,f(x))
podle x dostáváme
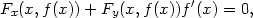
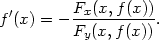
Příklad 8.1. i) Určete rovnici tečny a normály ke křivce dané rovnicí x3 + y3 − 2xy = 0 v bodě [1,1] (viz úvodní komentář).
Řešení. Označme F(x,y) = x3 + y3 − 2xy. Platí Fy(x,y) = 3y2− 2x,Fy(1,1) = 1≠ 0, jsou tedy splněny všechny předpoklady věty, tj. rovností x3 + y3 − 2xy = 0 je v jistém okolí bodu [1,1] určena implicitně funkce jedné proměnné y = f(x), pro jejíž derivaci v bodě x = 1 dostáváme
![Fx(1,1) 3x2 − 2y f′(1) = −------- = − --2-----∣[x,y]=[1,1] = − 1. Fy(1,1) 3y − 2x](diferencialni-pocet849x.png)
ii) Určete, ve kterých bodech křivky x2 + y2 −xy − 1 = 0 je tečna rovnoběžná s osou x, resp. y.
Řešení. Stejně jako
v předchozím příkladu zjistíme, že ve všech bodech, kde
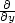 [x2
+ y2
− xy −
1] = 2y −
x≠0, je
rovnicí x2 +
y2 −xy
− 1
= 0 implicitně určena jistá funkce proměnné x. Pro její derivaci platí
[x2
+ y2
− xy −
1] = 2y −
x≠0, je
rovnicí x2 +
y2 −xy
− 1
= 0 implicitně určena jistá funkce proměnné x. Pro její derivaci platí
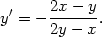
 =0, musí proto platit 2x−y
= 0. Protože hledaný bod leží na
křivce x2 +
y2 −xy
− 1
= 0, dostáváme systém rovnic
=0, musí proto platit 2x−y
= 0. Protože hledaný bod leží na
křivce x2 +
y2 −xy
− 1
= 0, dostáváme systém rovnic
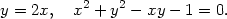

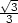 , y =
, y = 
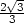 , tedy tečna ke křivce je vodorovná v bodech
[
, tedy tečna ke křivce je vodorovná v bodech
[
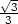 ,
,
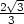 ].
].
Při určení bodů, kde je tečna rovnoběžná
s osou y, postupujeme
podobně. Tečna může být svislá pouze v bodech, kde je
jmenovatel zlomku vyjadřující y nulový. (Ke
stejnému výsledku dojdeme, jestliže se na rovnici x2
+ y2
− xy −
1 = 0 díváme jako na rovnici
určující implicitně x jako
funkci proměnné y.) Obdržíme
systém rovnic
nulový. (Ke
stejnému výsledku dojdeme, jestliže se na rovnici x2
+ y2
− xy −
1 = 0 díváme jako na rovnici
určující implicitně x jako
funkci proměnné y.) Obdržíme
systém rovnic


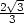 ,
,
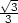 ], v nichž je tečna ke křivce
svislá.
], v nichž je tečna ke křivce
svislá.
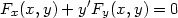 |
(8.2) |
a z této rovnice vypočteme y .
.
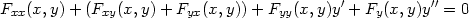

 . Dalším
derivováním poslední rovnice odvodíme vztah pro y
. Dalším
derivováním poslední rovnice odvodíme vztah pro y

 atd.
atd.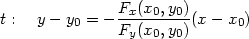
Příklad 8.2.
Řešení. Rovnici tečny jsme vypočítali v Příkladu 8.1 i) podle vzorce o derivaci funkce dané implicitně.
Nyní postupujme jako při odvození tohoto
vzorce. Derivujeme-li rovnici x3
+ y3
− 2xy
= 0 podle x a uvážíme-li, že y je funkce proměnné x, dostáváme 3x2
+ 3y2y −
2y −
2xy
−
2y −
2xy = 0. Dalším derivováním podle x obdržíme 6x
+ 6y(y
= 0. Dalším derivováním podle x obdržíme 6x
+ 6y(y )2
+ 3y2y
)2
+ 3y2y
 − 2y
− 2y −
2y
−
2y −
2xy
−
2xy
 = 0 a odtud
= 0 a odtud
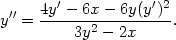
 = −1 (tato
hodnota je vypočítána při výpočtu tečny), dostaneme y
= −1 (tato
hodnota je vypočítána při výpočtu tečny), dostaneme y
 (1) = −16, což
znamená, že křivka leží v okolí bodu [1,1] pod
tečnou (neboť implicitně určená funkce je v bodě x = 1
konkávní).
(1) = −16, což
znamená, že křivka leží v okolí bodu [1,1] pod
tečnou (neboť implicitně určená funkce je v bodě x = 1
konkávní).
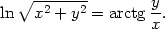 |
(8.3) |
Řešení. Derivováním rovnosti implicitně zadávající y jako funkci proměnné x dostáváme

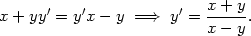
 =0 máme
x= −
y a dosazením do (8.3)
dostáváme ln
=0 máme
x= −
y a dosazením do (8.3)
dostáváme ln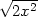 = arctg(−1) a
odtud x =
= arctg(−1) a
odtud x = 
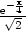 ,y =
,y = 
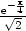 . Nyní vypočteme y
. Nyní vypočteme y
 v nalezených stacionárních bodech. Derivujeme-li rovnici
x + yy
v nalezených stacionárních bodech. Derivujeme-li rovnici
x + yy = y
= y x −
y „implicitně“ podle
x (jiná možnost, vedoucí
samozřejmě ke stejnému výsledku, je derivovat podle x zlomek
x −
y „implicitně“ podle
x (jiná možnost, vedoucí
samozřejmě ke stejnému výsledku, je derivovat podle x zlomek 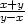 ), dostáváme 1 +
(y
), dostáváme 1 +
(y )2
+ yy
)2
+ yy
 = y
= y
 x +
y
x +
y − y
− y . Odtud
. Odtud
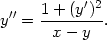

 (−
(−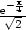 ) <
0, y
) <
0, y
 (
(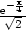 ) >
0, tedy v bodě x =
−
) >
0, tedy v bodě x =
−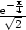 má implicitně zadaná funkce lokální maximum a
v bodě x =
má implicitně zadaná funkce lokální maximum a
v bodě x = 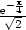 lokální minimum.
(Geometricky se o správnosti výpočtu můžeme přesvědčit
náčrtkem křivky, přejdeme-li v (8.3) k polárním
souřadnicím x = r
cos
lokální minimum.
(Geometricky se o správnosti výpočtu můžeme přesvědčit
náčrtkem křivky, přejdeme-li v (8.3) k polárním
souřadnicím x = r
cos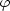 , y
= r sin
, y
= r sin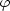 , pak pro
, pak pro
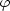
 (−
(−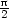 ,
,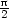 ) dostáváme část logaritmické spirály
r =
e2
) dostáváme část logaritmické spirály
r =
e2 a pro
a pro 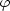
 (
(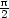 ,
,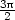 ) křivku, která je středově symetrická podle
počátku s touto spirálou.)
) křivku, která je středově symetrická podle
počátku s touto spirálou.)
V úvahách prováděných na začátku
předchozího odstavce se můžeme snadno „posunout“ o dimenzi
výše. Uvažujme v  3
množinu M = {[x,y,z]
3
množinu M = {[x,y,z]

 3
: F(x,y,z) =
0}, kde F je nějaká funkce tří proměnných. Za
celkem přirozených předpokladů na funkci F (např. diferencovatelnost) je
M nějaká plocha
v
3
: F(x,y,z) =
0}, kde F je nějaká funkce tří proměnných. Za
celkem přirozených předpokladů na funkci F (např. diferencovatelnost) je
M nějaká plocha
v  3 a můžeme si klást otázku, jaká je rovnice
tečné roviny k ploše M
v bodě [x0,y0,z0]
3 a můžeme si klást otázku, jaká je rovnice
tečné roviny k ploše M
v bodě [x0,y0,z0]
 M, popř. zda v okolí tohoto bodu je
plocha pod, nebo nad tečnou rovinou. Lze-li z rovnice
F(x,y,z) =
0 vypočítat proměnnou z,
můžeme použít postup ze čtvrté kapitoly. Pokud toto není možné,
zcela analogicky jako pro funkci dvou proměnných můžeme odvodit
podmínku, kdy je množina M
v okolí bodu [x0,y0,y0] totožná
s grafem nějaké funkce dvou proměnných z =
f(x,y),
tj. v okolí bodu [x0,y0,z0] platí
F(x,y,f(x,y)) =
0 a f(x0,y0) =
z0. Pokud taková funkce existuje, řekneme, že
je v okolí bodu [x0,y0,z0]
implicitně zadána rovnicí
F(x,y,z) =
0.
M, popř. zda v okolí tohoto bodu je
plocha pod, nebo nad tečnou rovinou. Lze-li z rovnice
F(x,y,z) =
0 vypočítat proměnnou z,
můžeme použít postup ze čtvrté kapitoly. Pokud toto není možné,
zcela analogicky jako pro funkci dvou proměnných můžeme odvodit
podmínku, kdy je množina M
v okolí bodu [x0,y0,y0] totožná
s grafem nějaké funkce dvou proměnných z =
f(x,y),
tj. v okolí bodu [x0,y0,z0] platí
F(x,y,f(x,y)) =
0 a f(x0,y0) =
z0. Pokud taková funkce existuje, řekneme, že
je v okolí bodu [x0,y0,z0]
implicitně zadána rovnicí
F(x,y,z) =
0.
Zcela analogická je situace, kdy je rovnicí F(x1,…,xn,y) = 0 v okolí bodu [x∗,y] = [x1∗,…,xn∗,y] implicitně určena funkce n proměnných y = f(x1,…,xn). Přistoupíme proto k formulaci existenčního tvrzení přímo pro tento obecný případ. Důkaz tvrzení neuvádíme, protože je v podstatě totožný s případem, kdy x je skalární proměnná.
Věta 8.3. Nechť funkce F
:  n+1
n+1 
 ,
M = {[x,y] =
[x1,…,xn,y]
,
M = {[x,y] =
[x1,…,xn,y]

 n+1, F(x,y) =
0}, [x∗,y∗]
n+1, F(x,y) =
0}, [x∗,y∗]
 M a F
je spojitá na množině R
= {[x,y] =
[x1,…,xn,y] :
M a F
je spojitá na množině R
= {[x,y] =
[x1,…,xn,y] :
 xi
− xi∗
xi
− xi∗ < a,i =
1,…,n,
< a,i =
1,…,n,  y
− y∗
y
− y∗ < a}. Dále předpokládejme, že F má spojitou parciální derivaci
Fy v bodě [x∗,y∗] a
< a}. Dále předpokládejme, že F má spojitou parciální derivaci
Fy v bodě [x∗,y∗] a
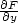 (x∗,y∗)≠0. Pak
existuje okolí bodu [x
∗,y∗],
v němž je rovnicí F(x,y) =
F(x1…,xn,y) = 0
implicitně určena právě jedna spojitá funkce y =
f(x) =
f(x1,…,xn).
(x∗,y∗)≠0. Pak
existuje okolí bodu [x
∗,y∗],
v němž je rovnicí F(x,y) =
F(x1…,xn,y) = 0
implicitně určena právě jedna spojitá funkce y =
f(x) =
f(x1,…,xn).
Má-li navíc funkce F v bodě [x∗,y∗] spojité
parciální derivace 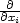 F, má implicitně určená funkce f v bodě x∗
= [x1∗…,xn∗]
parciální derivace a platí
F, má implicitně určená funkce f v bodě x∗
= [x1∗…,xn∗]
parciální derivace a platí
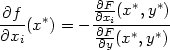
Příklad 8.3. i) Určete rovnici tečné roviny v bodě [1,0,1] k ploše určené rovnicí x3 + y3 + z3 − 3xyz − x − y − z = 0.
Řešení. Určíme parciální derivace implicitně zadané funkce z = z(x,y). Derivováním zadávající rovnice podle x a podle y (uvážíme při tom, že z je funkcí proměnných x a y) dostáváme
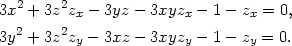
|
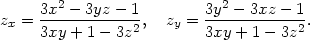
ii) Rozhodněte, zda plocha v  3
daná rovnicí x + y2
+ z3
+ z −
4 = 0 leží v okolí bodu
[1,1,1] pod
tečnou rovinou, nebo nad tečnou rovinou sestrojenou v tomto
bodě.
3
daná rovnicí x + y2
+ z3
+ z −
4 = 0 leží v okolí bodu
[1,1,1] pod
tečnou rovinou, nebo nad tečnou rovinou sestrojenou v tomto
bodě.
Řešení. Postupem popsaným ve Větě 8.3 určíme parciální derivace v bodě [1,1] funkce z = z(x,y). Dostáváme
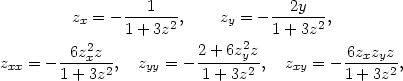
|
 , zy =
−
, zy =
− , zxx =
−
, zxx =
−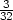 , zxy =
−
, zxy =
−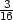 , zyy =
−
, zyy =
−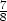 . Tečná rovina v bodě [1,1,1] má
rovnici z − 1 =
−
. Tečná rovina v bodě [1,1,1] má
rovnici z − 1 =
−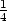 (x −
1) −
(x −
1) −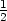 (y
− 1).
(y
− 1).
Nyní použijeme tvrzení uvedené v Poznámce 6.3 . Platí

a zxx(1,1) =
−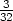 . Proto plocha určená rovnicí x +
y2 +
z3 +
z − 4 = 0
leží v okolí bodu [1,1,1] pod
tečnou rovinou v tomto bodě.
. Proto plocha určená rovnicí x +
y2 +
z3 +
z − 4 = 0
leží v okolí bodu [1,1,1] pod
tečnou rovinou v tomto bodě.
iii) Určete lokální extrémy funkce z =
f(x,y)
určené implicitně rovnicí F(x,y,z) =
x2 +
y2 +
z2 −
xz −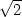 yz
= 1.
yz
= 1.
Řešení. Derivováním zadávající rovnosti podle x a y dostáváme
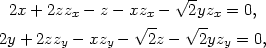
|
(8.4) |
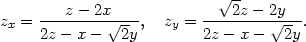
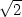 y, tedy y =
y, tedy y =
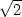 x. Dosazením do
zadávající rovnice obdržíme dvojici stacionárních bodů P1
= [1,
x. Dosazením do
zadávající rovnice obdržíme dvojici stacionárních bodů P1
= [1,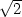 ,2],
P2 =
[−1,−
,2],
P2 =
[−1,−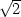 ,−2].
V těchto bodech je Fz≠0, tedy
v jejich okolí je implicitně určena jistá funkce z =
f(x,y).
Derivováním (8.4)
vypočteme parciální derivace 2. řádu ve stacionárních bodech
,−2].
V těchto bodech je Fz≠0, tedy
v jejich okolí je implicitně určena jistá funkce z =
f(x,y).
Derivováním (8.4)
vypočteme parciální derivace 2. řádu ve stacionárních bodech
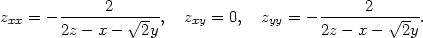
Podobným způsobem jako v Poznámce 8.2 iii) lze dokázat následující tvrzení.
Ve vektorovém zápisu je uvedený vztah
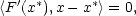
 .,.
.,. značí skalární součin v
značí skalární součin v  n), tedy
vektor F
n), tedy
vektor F (x∗) = (
(x∗) = (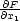 (x∗),…,
(x∗),…,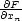 (x∗)) je normálovým vektorem v bodě
x∗ k plo
še F(x) = 0.
(x∗)) je normálovým vektorem v bodě
x∗ k plo
še F(x) = 0.
Příklad 8.4. Určete rovnici tečné nadroviny v bodě [1,1,…,1] k (n − 1)-rozměrné ploše dané rovnicí x1 + x22 + ⋯ + xnn − n = 0.
Řešení. Platí 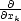
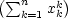 = kxkk−1. Odtud
dosazením do (8.5
)
dostáváme rovnici
tečné nadroviny
= kxkk−1. Odtud
dosazením do (8.5
)
dostáváme rovnici
tečné nadroviny
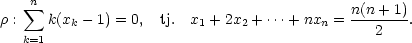
Poznámka 8.3. Derivace vyšších řádů funkce y
= f(x1,…,xn) zadané
implicitně rovnicí
F(x1,…,xn,y) = 0 vypočteme úplně stejně
jako pro
dvě proměnné. Například parciální derivaci
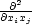 f(x) vypočteme
tak, že rovnici
F(x1,…,xn,y) = 0 derivujeme nejprve
podle xi a pak podle
xj (přitom vždy bereme
v úvahu,
že
y je
funkcí vektorové
proměnné x = [x1,…,xn]).
f(x) vypočteme
tak, že rovnici
F(x1,…,xn,y) = 0 derivujeme nejprve
podle xi a pak podle
xj (přitom vždy bereme
v úvahu,
že
y je
funkcí vektorové
proměnné x = [x1,…,xn]).
V tomto odstavci se zabýváme nejobecnějším případem. Nechť je dáno m funkcí Fi , n + m proměnných x = [x1,…,xn], y = [y1,…,ym], i = 1,…,m a uvažujme systém rovnic
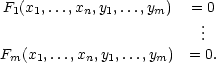 |
(8.6) |
Na m-tici
funkcí F1,…,Fm se
můžeme
dívat
jako na zobrazení
z  n+m
n+m 
 m,
které
označíme
m,
které
označíme  . Pak F1,…,Fm jsou
složky tohoto zobrazení, tj.
. Pak F1,…,Fm jsou
složky tohoto zobrazení, tj.  = {F1,…,Fm}. Podobně
jako v předchozích dvou
odstavcích označme M = {[x,y]
= {F1,…,Fm}. Podobně
jako v předchozích dvou
odstavcích označme M = {[x,y] 
 n+m :
n+m :  (x,y) = 0} a nechť
[x∗,y∗]
(x,y) = 0} a nechť
[x∗,y∗]  M. Jestliže existuje
okolí bodu [x∗,y∗]
M. Jestliže existuje
okolí bodu [x∗,y∗] 
 n+m
n+m  ([x∗,y∗]) =
([x∗,y∗]) =
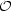 (x∗)
(x∗) 
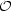 (y∗) a zobrazení
(y∗) a zobrazení
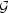 :
:  m
m

 n takové, že pro
každé [x,y]
n takové, že pro
každé [x,y] 
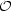 ([x∗,y∗]) je množina
bodů [x,y]
([x∗,y∗]) je množina
bodů [x,y]  M
totožná s množinou
bodů [x,
M
totožná s množinou
bodů [x,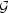 (x)],x
(x)],x 
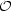 (x∗), řekneme, že zobrazení
(x∗), řekneme, že zobrazení
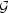 je
v okolí bodu
[x∗,y∗] implicitně
určeno rovnicí
je
v okolí bodu
[x∗,y∗] implicitně
určeno rovnicí
 (x,y) = 0.
(x,y) = 0.
Hledáme
podmínky pro existenci implicitně zadaného
zobrazení. Jinými slovy, chceme v okolí
bodu [x∗,y∗] ze systému rovnic
(8.6) jednoznačně určit proměnné y1,…,ym v z
ávislosti na x1,…,xn, neboli
hledáme podmínky, za
kterých
systém rovnic (8.6) určuje
v okolí bodu
[x∗,y∗]  M nějaké spojité
zobrazení
M nějaké spojité
zobrazení 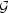 :
:
 m
m

 n.
Současně odvodíme vzorec pro Jacobiho
matici tohoto implicitně
určeného
zobrazení.
n.
Současně odvodíme vzorec pro Jacobiho
matici tohoto implicitně
určeného
zobrazení.
Čtenáři doporučujeme při čtení výsledků tohoto odstavce dosadit m = n = 1 (tj. všechny matice a vektory se redukují na skalární hodnoty) a porovnat je s tvrzeními z odstavce 8.1. Takto zjistíme, že když „zapomeneme“, že x,y jsou vektorové proměnné, je tvrzení Věty 8.5 stejné jako ve Větách 8.1 , 8.2 .
Věta 8.5. Nechť  = {F1,…,Fm} je spojité
zobrazení na
množině R = {[x,y]
= {F1,…,Fm} je spojité
zobrazení na
množině R = {[x,y] 
 n+m : [x,y]
n+m : [x,y] 
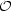 a(x∗)
a(x∗) 
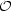 a(y∗)}, nechť matice
a(y∗)}, nechť matice
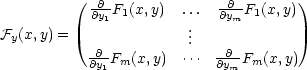
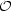 ([x∗,y∗]) =
([x∗,y∗]) =
 (x∗)
(x∗) 
 (y∗) bodu [x∗,y∗] takové, že
rovnicí
(y∗) bodu [x∗,y∗] takové, že
rovnicí  (x,y) = 0 je v tomto
okolí bodu [x∗,y∗] určeno jediné
spojité zobrazení
(x,y) = 0 je v tomto
okolí bodu [x∗,y∗] určeno jediné
spojité zobrazení
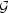 :
: 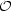 (x∗)
(x∗) 
 (y∗), tj. pro
x
(y∗), tj. pro
x 
 (x∗) je
(x∗) je  (x,
(x,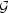 (x)) = 0.
(x)) = 0.
Jsou-li navíc v bodě [x∗,y∗] spojité prvky matice
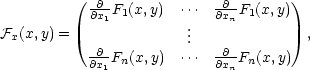
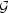 spojité
v x∗
a platí
spojité
v x∗
a platí
![𝒢 ′(x∗) = [ℱy(x∗,y∗)]−1ℱx(x∗,y∗).](diferencialni-pocet914x.png)
Důkaz.
Označíme-li d
= det y(x∗,y∗) a budeme-li s maticemi
y(x∗,y∗) a budeme-li s maticemi  y,
y, x
manipulovat v podstatě
stejně jako
v důkazu
Vět 8.1
, 8.2
,
zjistíme, že důkaz těchto
vět
„projde“ i v maticovém případě. Se všemi technickými podrobnostmi je tato
myšlenka realizována ve
skriptu [N2].
□
x
manipulovat v podstatě
stejně jako
v důkazu
Vět 8.1
, 8.2
,
zjistíme, že důkaz těchto
vět
„projde“ i v maticovém případě. Se všemi technickými podrobnostmi je tato
myšlenka realizována ve
skriptu [N2].
□
Nyní se budeme
zabývat definicí
tečného a
normálového prostoru k podmnožinám v  n,
které jsou definovány jako
množina řešení jistého systému rovnic. Podrobně,
nechť
n,
které jsou definovány jako
množina řešení jistého systému rovnic. Podrobně,
nechť  :
:  n
n

 m,
m < n, fi
:
m,
m < n, fi
:  n
n 
 , i = 1,…,m jsou složky tohoto zobrazení a označme M =
, i = 1,…,m jsou složky tohoto zobrazení a označme M =  −1(0) =
{x
= [x1,…,xn]
−1(0) =
{x
= [x1,…,xn] 
 n :
n :  (x) = 0}, tj. M je množina řešení systému rovnic
(x) = 0}, tj. M je množina řešení systému rovnic
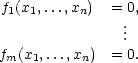
Jako model
uvažujme dvojici rovnic x2
+ y2
+ z2
− 1 =
0, x + y + z = 0. Z geometrického významu je
zřejmé, že množinou
M v  3 určenou touto dvojicí
rovnic je kružnice,
která je průsečíkem sféry x2
+ y2
+ z2
= 1 s rovinou
x +
y +
z =
0. Je-li [x∗,y∗,z∗]
3 určenou touto dvojicí
rovnic je kružnice,
která je průsečíkem sféry x2
+ y2
+ z2
= 1 s rovinou
x +
y +
z =
0. Je-li [x∗,y∗,z∗]  M, pak je přirozené
nazvat směrový vektor
tečny
ke kružnici v bodě
[x∗,y∗,z∗] tečným prostorem k M
v bodě
[x∗,y∗,z∗] a ortogonální doplněk k tomuto jednorozměrnému podprostoru
normálovým
prostorem. Je zřejmé, že
normálový prostor k M
v [x∗,y∗,z∗] je lineární podprostor v
M, pak je přirozené
nazvat směrový vektor
tečny
ke kružnici v bodě
[x∗,y∗,z∗] tečným prostorem k M
v bodě
[x∗,y∗,z∗] a ortogonální doplněk k tomuto jednorozměrnému podprostoru
normálovým
prostorem. Je zřejmé, že
normálový prostor k M
v [x∗,y∗,z∗] je lineární podprostor v  3,
který je generován
normálovými vektory ke kulové
ploše a
k rovině. Z tohoto pohledu je přirozená
následující definice.
3,
který je generován
normálovými vektory ke kulové
ploše a
k rovině. Z tohoto pohledu je přirozená
následující definice.
Poznámka 8.4. i)
V literatuře věnované
diferenciální geometrii a
globální analýze (viz např. [S])
bývá tečný prostor k podmnožinám v  n definován
poněkud odlišně, pro
množiny zadané
systémem rovnic
při
splnění předpokladů
z předchozí
definice je však tento objekt
totožný s námi
definovaným tečným prostorem. Podrobněji o této problematice pojednává skriptum [N2]
a monografie [S].
n definován
poněkud odlišně, pro
množiny zadané
systémem rovnic
při
splnění předpokladů
z předchozí
definice je však tento objekt
totožný s námi
definovaným tečným prostorem. Podrobněji o této problematice pojednává skriptum [N2]
a monografie [S].
ii) Předpoklad na hodnost
matice 
 (x∗) v Definici 8.2 nelze vypustit. Uvažujme v
(x∗) v Definici 8.2 nelze vypustit. Uvažujme v  2 množinu M = {[x,y] : f(x,y) = x2 − y2
= 0, y
≥ 0}. Pak evidentně
M je
tvořena dvojicí
polopřímek y
2 množinu M = {[x,y] : f(x,y) = x2 − y2
= 0, y
≥ 0}. Pak evidentně
M je
tvořena dvojicí
polopřímek y  x = 0 a v počátku (kde fx(0,0) = 0 = fy(0,0)) tečnu nelze sestrojit, neboť křivka zde
má „hrot“.
x = 0 a v počátku (kde fx(0,0) = 0 = fy(0,0)) tečnu nelze sestrojit, neboť křivka zde
má „hrot“.
Příklad 8.5. i) Určete parametrickou rovnici tečny v bodě [x0,y0,z0], z0 > 0 k prostorové křivce, která je průsečíkem kulové plochy x2 + y2 + z2 = 4 s válcovou plochou x2 + y2 − 2x = 0 (tzv. Vivianiho křivka2).
Řešení. Normálové vektory
k jednotlivým
plochám v bodě
[x0,y0,z0] jsou n1
= (2x0,2y0,2z0) pro kouli a n2
= (2x0
− 2,2y0,0) pro válec. Normálový prostor ke
křivce je generován těmito
dvěma vektory
(všimněte si, že v bodě
[4,0,0] jsou lineárně závislé, zde
má
křivka
hrot – načrtněte si
obrázek). Jejich vektorový součin u = (−y0z0,z0(x0
− 1),y0) je směrovým vektorem
tečny, která
má
tedy rovnici t
: [x,y,z] = [x0,y0,z0] +  (−y0z0,z0(x0
− 1),y0),
(−y0z0,z0(x0
− 1),y0), 

 .
.
ii) Určete Jacobiho matici
zobrazení F :  2
2

 2: u = u(x,y),v = v(x,y), které
je v okolí
bodu [x∗,y∗,u∗,v∗] =
[1,0,1,0] určeno
implicitně dvojicí
rovnic
2: u = u(x,y),v = v(x,y), které
je v okolí
bodu [x∗,y∗,u∗,v∗] =
[1,0,1,0] určeno
implicitně dvojicí
rovnic
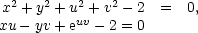 |
(8.7) |
Řešení. Označme M množinu
bodů v  4,
které vyhovují
zadávající dvojici rovnic.
Přímým
dosazením snadno ověříme, že vskutku
[x∗,y∗,u∗,v∗]
4,
které vyhovují
zadávající dvojici rovnic.
Přímým
dosazením snadno ověříme, že vskutku
[x∗,y∗,u∗,v∗]  M a derivováním
systému rovnic podle x
(s tím, že u,v jsou funkce
proměnných x,y) dostáváme (po
jednoduché úpravě)
M a derivováním
systému rovnic podle x
(s tím, že u,v jsou funkce
proměnných x,y) dostáváme (po
jednoduché úpravě)
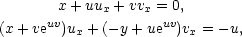 |
 2 systémy většinou nejrychlejší metoda řešení)
2 systémy většinou nejrychlejší metoda řešení)
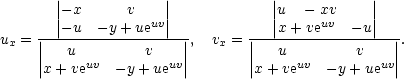
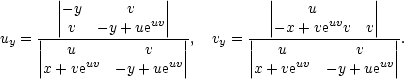
Dosazení
m bodu [x∗,y∗,u∗,v∗] do těchto vyjádření vidíme, že
systém (8.7
)
definuje implicitně v okolí
bodu [x∗,y∗,u∗,v∗] opravdu zobrazení
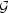 : [x,y]↦[u,v] (neboť
jmenovatel všech
zlomků je nenulový) a
platí ux
= −1, vx = 0, uy
= 0,
vy = 0, tedy det
: [x,y]↦[u,v] (neboť
jmenovatel všech
zlomků je nenulový) a
platí ux
= −1, vx = 0, uy
= 0,
vy = 0, tedy det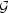
 (x∗,y∗) =
0.
(x∗,y∗) =
0.
Cvičení 
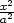 +
+ 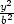 −
−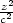 = 1 nejsou splněny
předpoklady Věty 8.3
o existenci implicitní funkce
z = f(x,y)?
= 1 nejsou splněny
předpoklady Věty 8.3
o existenci implicitní funkce
z = f(x,y)?
8.2. Vypočtěte y funkce
y = f(x)
zadanou implicitně rovnicí:
funkce
y = f(x)
zadanou implicitně rovnicí:
| a) x − y2 = lny | b) xy = yx, kde x > 0,y > 0. |
8.3. Určete rovnici tečny ke kuželosečce:
8.4. Na elipse o rovnici x2 + 3y2 − 2x + 6y − 8 = 0 najděte body, v nichž je normála rovnoběžná s osou y.
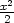 − 3y
+ 2z2
= 0 v bodě T =
[2,
− 3y
+ 2z2
= 0 v bodě T =
[2,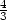 ,−1].
,−1]. : x
+ 4y +
6z = 0.
: x
+ 4y +
6z = 0. : x
− y +
2z = 0.
: x
− y +
2z = 0.
8.7. Určete parciální derivace 1. a 2. řádu funkce z = z(x,y) dané implicitně rovnicí:
a) x
+ y +
z =
e−(x+y+z), b) z
= 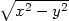 tg
tg 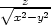 . . |
8.8. Najděte stacionární body funkce y = y(x) dané implicitně rovnicí
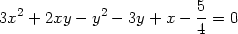
8.9. Najděte stacionární body funkce z = f(x,y) a zjistěte, zda jsou v těchto bodech lokální extrémy:
∗
Nic na světě nemůže nahradit vytrvalost. Nenahradí ji ani talent; nic není běžnější než neúspěšný člověk s talentem. Ani genialita; nedoceněný génius je téměř přísloveč ný. Pouze vytrvalost a odhodlání jsou všemocné . (C. Coolidge)
∗
1Doslovný český překlad slova implicitní je nerozvinutý, v něčem obsažený.
2Vincenzo Viviani (1622–1703), italský matematik, žák G. Galileiho
3Gabriel Cramer (1704–1752), švýcarský matematik
[Další] [Předchozí] [Předchozí – na konec] [Na začátek] [Výše]