Lékařská fakulta Masarykovy univerzity
Mgr. David Severa, Mgr. Petr Veselý, DiS., Ph.D., Mgr. Pavel Beneš, Ph.D
Základní rozdělení subjektivních metod korekce refrakčních vad
Jacksonovy zkřížené cylindry
Jednou z nejpoužívanějších subjektivních metod při korekci astigmatizmu je metoda pomocí Jacksonových zkřížených cylindrů (JZC). Tato metoda historicky vychází z tzv. Stokesovy čočky, která byla v 19. století jednou z prvních optických pomůcek určených k změření parametrů astigmatizmu. Jednalo se o kombinaci rotačního plankonvexního a plankonkávního cylindru s plynulým nárůstem účinku. Cílem byla snaha o určení osy korekčního účinku cylindru. JZC byly uvedeny Edwardem Jacksonem (1887) nejprve jako nástroj pro určení optické mohutnosti korekčního cylindru, teprve později byl prokázán jejich přínos při určování orientace osy cylindru. Hlavním rozdílem oproti Stokesově čočce bylo fixní, kolmé uspořádání os cylindrů. Tyto pomůcky byly přirozenou odpovědí na vzrůstající schopnosti praktiků diagnostikovat a dále korigovat typ ametropie. I vzrůstající požadavky na přesnost korekce tak byly hnací silou tohoto počínání. (Tasman a kol. 2006)
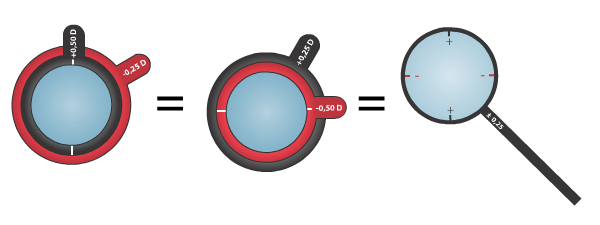
Jak už bylo naznačeno výše v textu, JZC konstrukčně představují spojný a rozptylný plancylindr, které jsou vůči sobě ve fixním kolmém uspořádání. Fakticky se nejedná o dva samostatné optické členy, nýbrž o jejich ekvivalent v podobě výbrusu jedné optické komponenty s jednou plochou sférickou a druhou cylindrickou. Oba hlavní řezy cylindrů vykazují stejnou hodnotu vrcholové lámavosti, avšak jeden z nich prošlé paprsky konverguje (spojný cylindr) a druhý diverguje (rozptylný cylindr). Při hodnocení lámavého účinku JZC na šíření rovnoběžných paprsků (tj. paprsků přicházejícím z nekonečna), se vychází ze znalostí o kolmém optickém účinku cylindru vůči jeho korekčnímu účinku. Osy korekčních účinků obou cylindrů jsou vždy graficky znázorněny nebo odlišeny pomocí znamének + a -, popř. pomocí barevných značek, které ideálně korespondují s barvami plancylindrů ze sady zkušebních čoček. Popsaný optický člen je zasazen do kulaté objímky, opatřené držátkem umístěným v místě mezi osami cylindrů. Toto umístění není náhodné, ale otočení držátka mezi prsty o 180° umožňuje rychlou a přesnou výměnu orientace os obou cylindrů. Snadnost manipulace bývá často podpořena vhodným profilem držátka, které je buďto kulaté, nebo čtyřhranné.
Obr. 4.1 Nákres konstrukce JZC
V praxi se mohou používat JZC o hodnotách ±0,12 D, ±0,25 D, ±0,37 D, ±0,50 D a ±0,75 D.
Cylindricko-cylindrické zápisy pro jednotlivé hodnoty JZC jsou:
+0,12 D cyl ax 90° komb. -0,12 D cyl ax 180°
+0,25 D cyl ax 90° komb. -0,25 D cyl ax 180°
+0,37 D cyl ax 90° komb. -0,37 D cyl ax 180°
+0,50 D cyl ax 90° komb. -0,50 D cyl ax 180°
+0,75 D cyl ax 90° komb. -0,75 D cyl ax 180°
Předřazení libovolného Jacksonova cylindru před oko se navodí sférický i cylindrický účinek. Vrcholovou lámavost JZC ±0,25 D lze ve sféro-cylindrickém zápisu popsat s rozptylnou hodnotou cylindru orientovanou ve 180° jako
sph +0,25 D komb. cyl -0,50 D ax 180°
nebo se spojnou hodnotou cylindru jako
sph -0,25 D komb. cyl +0,50 D ax 90°.
Pokud otočíme držátkem JZC kolem jeho osy, vyměníme tak orientaci rozptylného cylindru ze 180° na 90°, respektive z 90° na 180° a stejný zápis pro rozptylnou vrcholovou lámavost cylindru bude vypadat:
sph +0,25 D komb. cyl -0,50 D ax 90°
a pro spojnou vrcholovou lámavost
sph -0,25 D komb. cyl +0,50 D ax 180°.
Sférický ekvivalent každého JZC (vypočtený jako součet sférické hodnoty a poloviny hodnoty cylindru) je tedy roven nule! (Rutrle 2000)
Při hledání osy cylindru korigovaného oka dochází k vektorovému průmětu lomivých účinků cylindrů předřazeného JZC do skutečné osy očního astigmatizmu. Vyšetřovaný pak pouze vybírá, který z nabízených obrazů (tedy směrů se svou orientací, respektive účinkem) se blíží více finální astigmatické korekci.
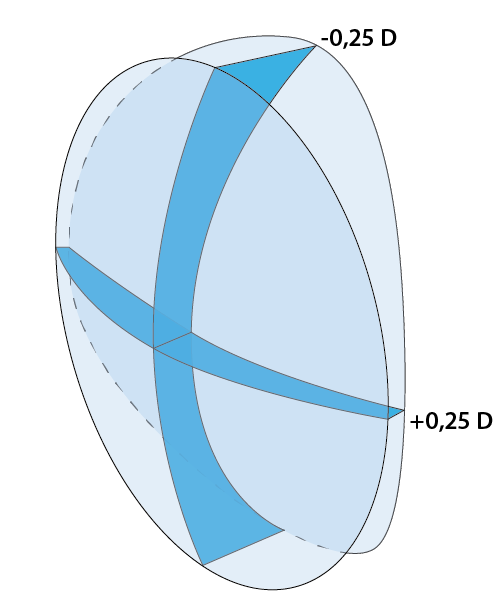
Je vhodné vyzdvihnout fakt, že plná hodnota optického účinku každého cylindru je vždy v kolmém směru na orientaci jeho osy korekčního účinku. V rozmezí těchto 90° dochází směrem od osy cylindru k lineárnímu zesilování refrakční hodnoty, od 0 D až po jeho maximální vrcholovou lámavost, tzn., že plancylinr -1,0 D bude mít ve své ose korekčního účinku skutečnou vrcholovou lámavost 0 D, ve 45°od osy -0,5 D a v kolmém směru plnou -1,0 D. (Tasman a kol. 2006; Linksz 1942)
Obr. 4.4 Optický účinek předřazeného plancylindru -1,0 D
Na příklad plancylindr -1,0 D bude orientován svým korekčním účinkem do osy 0°. Jeho vrcholovou lámavost v 0°, 45° a 90° jsme již uvedli. V praxi se ale nemusíme vždy spokojit s takto hrubými údaji. Obzvlášť v situacích, kdy je třeba stanovit účinek chybně určené astigmatické korekce, například u korekčního cylindru může vzniknout potřeba určit jeho vrcholovou lámavost v libovolném meridiánu. V takovém případě tak učiníme dosazením do vzorce
φn = φ. sin2 α
, kdy jn je optická mohutnost daného meridiánu, j je maximální hodnota optické mohutnosti uvažovaného plancylindru a α je úhel, pro který je optický účinek uvažován. (Tasman a kol. 2006; Linksz 1942)
V rámci problematiky řešení korekce astigmatizmu je třeba uvést několik základních souvisejících pojmů:
Sturmův konoid je geometricko-optický útvar, který se rozkládá mezi oběma fokálami pravidelně astigmatického optického systému oka. V případě astigmatizmu podle pravidla, kdy vertikální řez oka vykazuje větší lámavost, je horizontální fokála (tvořena vertikálně probíhajícími paprsky) ve větší vzdálenosti před sítnicí, nežli vertikální fokála (tvořena horizontálně probíhajícími paprsky). Oba hlavní řezy nekorigovaného astigmatického oka vytvoří na sítnici místo bodového obrazu eliptický útvar, což je prakticky obraz eliptického svazku dopadajících paprsků. Vertikální řez vytvoří vertikální elipsu, horizontální řez horizontální elipsu. Pro srovnání, v nekorigovaném lidském oku, zatíženém čistě sférickou vadou by došlo na sítnici k projekci rozptylného kroužku, nikoliv elipsy.
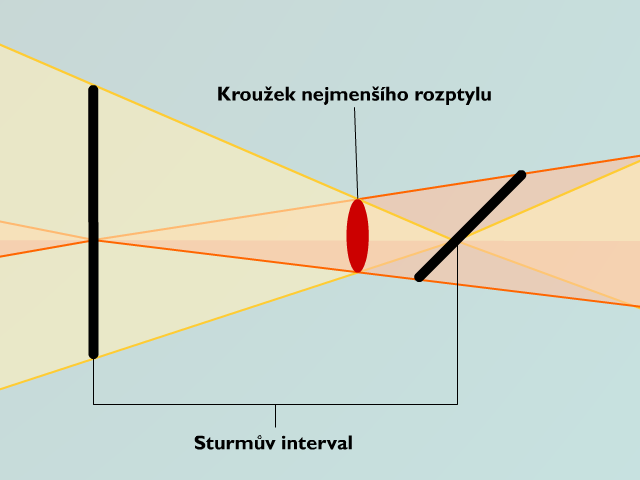
Obr. 4.5 Schéma astigmatizmu podle a proti pravidlu – ukázka Sturmova konoidu a kroužku nejmenšího rozptylu
Kroužek nejmenšího rozptylu (KNR) je kruhový svazek paprsků, nacházející se v dioptrickém středobodu Sturmova konoidu a je v předozadním směru ohraničen hlavními fokálami. (Grosvenor 2007)
Zamlžovací metoda
Druhou základní subjektivní metodou pro určení parametrů ametropie oka, respektive očního astigmatizmu je tzv. zamlžovací metoda. Z hlediska potřeby přístrojového vybavení jde o nenáročnou techniku. Některé fáze tohoto postupu se odehrávají ve fázi zamlžení, odtud tedy její charakteristický název. Hlavním účelem je vyřazení akomodace a snaha o navození “statického” optického systému. Očekávaným efektem je akomodačně nezkreslená astigmatická korekce. Paradoxně však tato fáze může být při nevhodně zvolené úrovni zamlžení pro některé klienty poněkud matoucí z hlediska nalezení ostřejší části astigmatického testu v celkově rozostřeném obrazu.
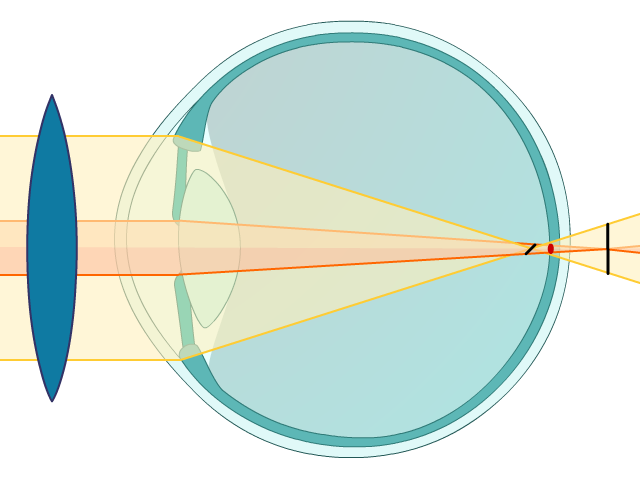
Obr. 4.6 Astigmatické oko s nejlepší sférickou korekcí (ast. smíšený)
Po nalezení nejlepší sférické korekce dochází k zamlžení odpovídající spojnou čočkou a navození složeného myopického astigmatizmu, respektive posunutí Sturmova konoidu před sítnici. Tento stav, kdy jsou obě fokály umístěny před sítnicí a neexistuje tak přímý spouštěč akomodace, je rozhodující pro akomodačně nezkreslený výsledek a lze jej předřazením vhodné spojky navodit z jakékoliv jiné formy pravidelného astigmatizmu.
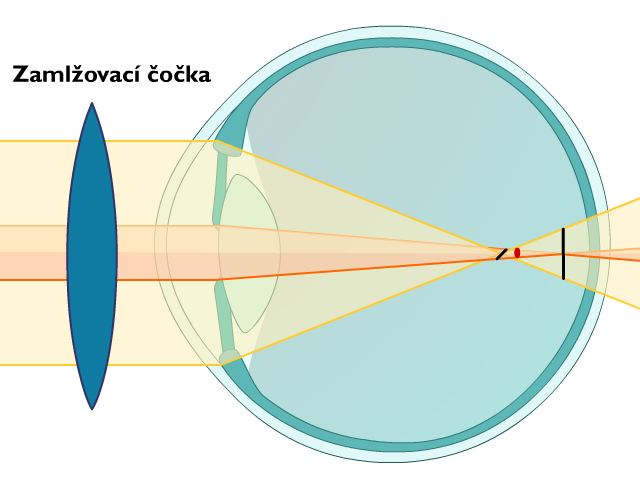
Obr. 4.7 Astigmatické oko po zamlžení (ast. složený hypermetropický převeden na ast. složený myopický)
Nejčastějšími testy, používanými pro určení osy a hodnoty očního astigmatizmu jsou astigmatická růžice a astigmatický vějíř. Ty slouží k determinaci nejostřejší/nejtmavší části testu a na základě tohoto poznatku je vyhodnocen předběžný směr osy astigmatizmu. Další fází je porovnání nejtmavších a nejsvětlejších partií testu, vedoucích k určení samotné hodnoty cylindru. Finální fází je potom jemné sférické dokorigování. (Grosvenor 2007)
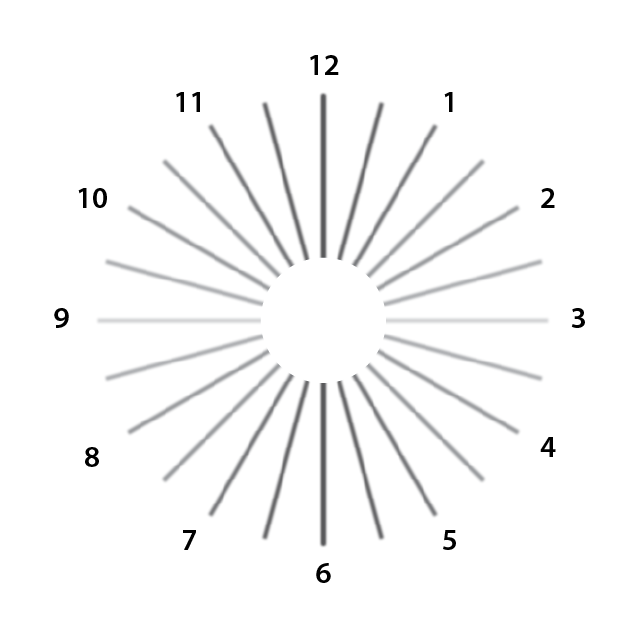
Obr. 4.8 Zobrazení astigmatické figury okem po zamlžení
Každé rameno astigmatické růžice si lze představit jako nekonečnou množinu jednotlivých bodů. V případě astigmatizmu podle pravidla je lámavost vertikálního řezu větší, tzn., že horizontální linie se promítne ve větší vzdálenosti před sítnicí. Ve fázi zamlžení dochází k posunu obou linií před sítnici s tím, že vertikální linie je blíž k sítnici. Bodový předmět se v tomto případě zobrazí jako vertikálně orientovaná elipsa. Pokud tímto okem zobrazíme zmíněný astigmatický test, všechny dílčí body každého z ramen se zobrazí jako vertikálně protažené elipsy. Rozdíl v tmavosti jednotlivých ramen růžice je dán silným překryvem bodů ve vertikálním rameni a slabým překryvem bodů v rameni horizontálním. Při práci s testovou figurou, kde každý z paprsků je tvořen trojitou tenkou čárou, může dotyčný jedinec vnímat jako horší to rameno, ve kterém z jeho pohledu dochází ke splynutí (bodovému slití) této „trojčáry“. Vzhledem k zamlžení a tím pádem vyloučení akomodační aktivity lze odpovědi pacienta považovat za poměrně stabilní. (Grosvenor 2007)
Mgr. Pavel Beneš, Ph.D. |
KOO, Lékařská fakulta Masarykovy univerzity |
Návrat na úvodní stránku webu, přístupnost |
| Servisní středisko pro e-learning na MU
| Fakulta informatiky Masarykovy univerzity, 2016
Centrum interaktivních a multimediálních studijních opor pro inovaci výuky a efektivní učení | CZ.1.07/2.2.00/28.0041