Překryv map
Úvod
Cílem této kapitoly je ukázat, jakým způsobem uchováváme v počítači data, která umožňují kreslit mapy, a jak z dat popisujících dvě různé mapy vytvářet nová data popisující překryv těchto dvou map. Co to je překryv map (map overlay), je znázorněno na následujícím obrázku, kde máme dvě mapy, červenou a modrou, a jejich překryv, který je černý.

Obrázek 3.1
Překryv červené a modré mapy vytvoří černou mapu
Popis map – rovinných podrozdělení
Mapou bude pro nás rovinné podrozdělení (plane subdivision), které se skládá z konečného počtu význačených bodů, úseček, které jsou spojnicemi těchto bodů a vzájemně se neprotínají ve vnitřních bodech, a souvislých oblastí, které jsou ohraničeny těmito úsečkami. Rovinná podrozdělení budeme popisovat pomocí tzv. dvojitě souvislých seznamů (doubly connected edge list).
Takový seznam se skládá ze tří tabulek, které popisují vrcholy, hrany a oblasti. Vrcholy (verteces) jsou význačné body rovinného podrozdělení. Hrana (edge) je úsečka rovinného podrozdělení společně s orientací. Vrchol, ze kterého hrana vychází, se nazývá počátek (origin). Ke každé hraně existuje hrana určená stejnou úsečkou ale s opačnou orientací. Tu nazýváme dvojčetem (twin) dané hrany. Třetím pojmem v popisu rovinných podrozdělení jsou oblasti (faces). Oblast, která sousedí zleva s danou hranou (co je zleva a co je zprava, je určeno orientací hrany) se nazývá přilehlá k dané hraně. Tento pojem umožňuje pro danou hranu $e$ jednoznačně definovat jejího následníka $\operatorname{next}(e)$ a předchůdce $\operatorname{prev}(e)$. Následník vychází z koncového bodu hrany $e$, má stejnou přilehlou oblast a mezi ním a hranou $e$ nejsou žádné jiné hrany s těmito vlastnostmi. Předchůdce je hrana, která končí v počátku hrany $e$, má rovněž stejnou přilehlou oblast a mezi ním a hranou $e$ nejsou žádné jiné hrany s předchozími dvěma vlastnostmi. Všechny tyto pojmy jsou demonstrovány na následujících obrázcích.
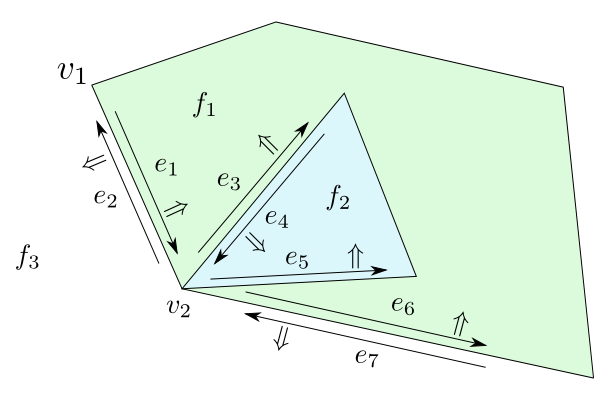
Obrázek 3.2
Hrana $e_1$ vychází z vrcholu $v_1$, hrana $e_2$ je dvojčetem hrany $e_1$, oblast $f_1$ je přilehlá k hranám $e_1$, $e_3$ a $e_6$. Následníkem hrany $e_1$ je $e_3$, nikoliv $e_6$. Předchůdcem hrany $e_2$ je $e_7$.
Dalším pojmem, který budeme používat, je pojem cyklu. Je to posloupnost hran $e_1,e_2,\dots,e_n, e_{n+1}$ taková, že $e_{i+1}$ je následníkem $e_i$ a $e_{n+1}=e_1$. Každá omezená oblast je ohraničena vnější hranicí, kterou při vhodné orientaci můžeme popsat jako cyklus hran, které mají danou oblast za přilehlou. Hovoříme o vnějším cyklu. Některé oblasti jsou ohraničeny i zevnitř jedním nebo více cykly. Orientaci jejich hran bereme opět tak, aby hrany byly k dané oblasti přilehlé. Nazýváme je vnitřní cykly.

Obrázek 3.3
Posloupnost hran $e_1,e_2,e_3,e_4,e_5,e_6,e_7$ je vnějším cyklem oblasti $f$, posloupnosti $e_8,e_9,e_{10}$ a $e_{11}, e_{12}, e_{13}, e_{14}$ jsou vnitřními cykly oblasti $f$.
Nyní můžeme popsat tabulky dvojitě souvislého seznamu podrobněji.
Vrcholy. V tabulce pro vrcholy je pro každý vrchol uvedeno jeho jméno, jeho souřadnice a ukazatel (pointer) na jednu vycházející hranu.
Hrany. Řádek v tabulce hran uvádí pro každou hranu její jméno, ukazatel na její počátek (bod, ze kterého vychází), ukazatel na její dvojče, ukazatel na přilehlou oblast, ukazatel na následníka a ukazatel na předchůdce.
Oblasti. Řádek v tabulce pro oblasti vypadá takto: jméno oblasti, ukazatel na jednu hranu z vnější hranice (existuje-li), ukazatel na jednu hrana z každého cyklu vnitřní hranice (existují-li).
Příklad jednoduchého rovinného podrozdělení a jeho popis pomocí dvojitě souvislého seznamu najdete na obrázku 3.4 a v následující tabulce.
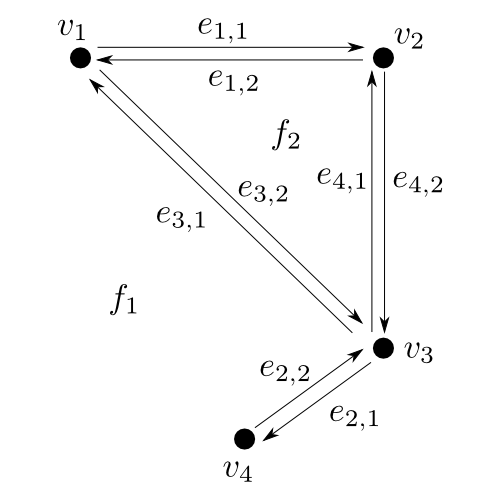
Obrázek 3.4
Příklad jednoduchého (i když trochu netypického) rovinného podrozdělení.
| Vrchol | souřadnice | vycházející hrana |
|---|---|---|
| $v_1$ | $(0,4)$ | $e_{1,1}$ |
| $v_2$ | $(2,4)$ | $e_{4,2}$ |
| $v_3$ | $(2,2)$ | $e_{3,1}$ |
| $v_4$ | $(1,1)$ | $e_{2,2}$ |
| Hrana | Počátek | Dvojče | Next | Prev | Přilehlá oblast |
|---|---|---|---|---|---|
| $e_{1,1}$ | $v_1$ | $e_{1,2}$ | $e_{4,2}$ | $e_{3,1}$ | $f_1$ |
| $e_{1,2}$ | $v_2$ | $e_{1,1}$ | $e_{3,2}$ | $e_{4,1}$ | $f_2$ |
| $e_{2,1}$ | $v_3$ | $e_{2,2}$ | $e_{2,2}$ | $e_{4,2}$ | $f_1$ |
| $e_{2,2}$ | $v_4$ | $e_{2,1}$ | $e_{3,1}$ | $e_{2,1}$ | $f_1$ |
| $e_{3,1}$ | $v_3$ | $e_{3,2}$ | $e_{1,1}$ | $e_{2,2}$ | $f_1$ |
| $e_{3,2}$ | $v_1$ | $e_{3,1}$ | $e_{4,1}$ | $e_{1,2}$ | $f_2$ |
| $e_{4,1}$ | $v_3$ | $e_{4,2}$ | $e_{1,2}$ | $e_{3,2}$ | $f_2$ |
| $e_{4,2}$ | $v_2$ | $e_{4,1}$ | $e_{2,1}$ | $e_{1,1}$ | $f_1$ |
| Oblast | Vnější cyklus | Vnitřní cykly |
|---|---|---|
| $f_1$ | - | $e_{3,1}$ |
| $f_2$ | $e_{1,2}$ | - |
Dvojitě souvislý seznam pro podrozdělení z obrázku 3.4
Popis pomocí dvojitě souvislého seznamu lze chápat jako minimální popis rovinného podrozdělení, ze kterého můžeme algoritmicky získat všechna další data v čase $O(n)$, kde $n$ je množství požadovaných dat. Chceme-li například najít všechny hrany vnějšího cyklu oblasti $f$, vezmeme jednu hranu z tabulky, k ní najdeme následníka, k následníkovi najdeme opět následníka a to provádíme tak dlouho, až se dostaneme k původní hraně. Díky tomu, že používáme ukazatele, lze hledání následníka považovat za krok časové náročnosti $O(1)$ a díky tomu je časová náročnost vyhledání všech hran vnější hranice rovna $O(n)$, kde $n$ je počet hran ve vnějším cyklu. Obdobným způsobem si jako jednoduché cvičení vyřešte tyto úkoly:
- najít všechny hrany vycházející z daného vrcholu $v$ a vypsat je v pořadí proti směru hodinových ručiček.
- najít všechny oblasti, které sousedí s vrcholem $v$ a vypsat je v pořadí proti směru hodinových ručiček. (Pozor, některé oblasti se mohou opakovat.)
Algoritmus pro překryv map
Mějme dána dvě rovinná podrozdělení $\mathcal{S}_1$ a $\mathcal{S}_2$, popsaná dvojitě souvislými seznamy $\mathcal{D}(\mathcal {S}_1)$ a $\mathcal{D}(\mathcal {S}_2)$. Cílem našeho algoritmu je vytvořit dvojitě souvislý seznam $\mathcal{D}$ pro překryv $\mathcal O(\mathcal S_1, \mathcal S_2)$ map $\mathcal{S}_1$ a $\mathcal{S}_2$. Navíc, u každé nové oblasti $f$ překryvu chceme uvést jména původních oblastí v $\mathcal{S}_1$ a $\mathcal{S}_2$, ve kterých oblast $f$ leží.
Pro zjednodušení budeme o rovinném podrozdělení $\mathcal{S}_1$ mluvit jako o červené mapě a o podrozdělení $\mathcal{S}_2$ jako o modré mapě. Tomu budou odpovídat i naše obrázky. Algoritmus začíná tím, že vytvoříme nový seznam $\mathcal D$ spojením dvojitě souvislých seznamů pro obě mapy. Úprava takto vytvořeného seznamu na dvojitě souvislý seznam překryvu má dva kroky. V prvém z nich doplňujeme a upravujeme záznamy v $\mathcal D$ týkající se vrcholů a hran tak, aby odpovídaly překryvu map. V druhé části provádíme úpravy týkající se oblastí.
Vrcholy a hrany
Tato část je založena na algoritmu zametací přímky pro nalezení průsečíků úseček, který byl podrobně popsán v předchozí kapitole. Jde však o jeho relativně pracnou modifikaci, proto v této kapitole provedeme popis algoritmu pouze slovně a jeho průběh budeme demonstrovat na příkladech. Popis pomocí pseudokódů by byl příliš dlouhý. Čtenáře odkazujeme na pseudokódy 4 – 10 v diplomové práci Dominika Janků:
https://is.muni.cz/auth/th/359588/fi_m/diplomka.pdfZačneme tím, že vytvoříme seznam úseček zadaných červenými a modrými hranami a jejich koncových vrcholů. (Pro zjednodušení předpokládejme, že průnikem červené a modré úsečky je buď bod, nebo prázdná množina, nebo jsou obě úsečky totožné. V posledním případě považujeme úsečky za jedinou úsečku, která je ovšem nositelem obou barev.) Ke každému vrcholu $p$ přiřadíme seznamy $L(p)$ a $U(p)$ se stejným významem jako v předchozí kapitole, přitom si budeme pamatovat, kolik úseček v těchto seznamech je červených a kolik modrých. Aktivujeme frontu událostí $\mathcal Q$, aby obsahovala všechny vrcholy, a binární vyvážený strom, který bude na začátku prázdný. Stejně jako v předchozí kapitole začněme provádět metodu zametací přímky.
Popíšeme algoritmus při průchodu událostí $p$. Jestliže množina $C(p)$ úseček, pro které je $p$ vnitřním bodem, je prázdná a sjednocení $L(p)\cup U(p)$ obsahuje pouze úsečky jedné barvy, neprovádíme v seznamu $\mathcal D$ žádné změny. Uvažujme případ, že $C(p)$ je neprázdná, a tudíž obsahuje úsečky obou barev. (Rozbor případu, že $C(p)$ je prázdná a $L(p)\cup U(p)$ obsahuje úsečky obou barev, je jednodušší a ponecháváme ho na čtenáři.) V tomto případě každou úsečku z $C(p)$ rozdělíme na dvě úsečky s koncovým bodem $p$ a ty zařadíme do $L(p)$ a $U(p)$. Novým úsečkám přiřadíme hrany – těm, které končí v $p$ přiřadíme hrany původní, těm, které začínají v $p$ hrany nové, viz následující obrázek.

Obrázek 3.5
Původní a nové označení úseček a hran.
Nyní provedeme v seznamu $\mathcal D$ tyto změny. Přidáme řádek pro vrchol $p$, upravíme řádky pro původní hrany odpovídající úsečkám, obsahujícím vrchol $p$, a přidáme řádky pro nové hrany. Pro určení nových následníků a předchůdců zmíněných hran uspořádáme pomocí binárního stromu nejdříve úsečky z $L(p)$ (to odpovídá poloze zametací přímky před událostí $p$) a potom uspořádáme úsečky z $U(p)$ (při poloze zametací přímky pod událostí $p$). Tím dostaneme uspořádání úseček z $L(p)$ a $U(p)$ kolem bodu $p$ ve směru hodinových ručiček. Konkrétní realizaci této myšlenky si ukažme na příkladu z obrázku 3.5
Pořadí úseček z $L(p)$ je $s_u\lt s'_u$. Pořadí úseček z $U(p)$ je $s'_l\lt s_l$. Tím je určeno pořadí úseček kolem bodu $p$ ve směru hodinových ručiček: $s_u, s'_u,s_l,s'_l$. Z tohoto pořadí určíme například, že následníkem hrany $e_1$ je $e_8$ a předchůdcem $e_5$ je $e_3$. Nový řádek pro vrchol $p$, upravený řádek pro hranu $e_1$ a nový řádek pro $e_5$ budou tedy vypadat takto
| Vrchol | souřadnice | vycházející hrana |
|---|---|---|
| $p$ | $(1,2)$ | $e_5$ |
| Hrana | Počátek | Dvojče | Next | Prev | Přilehlá oblast |
|---|---|---|---|---|---|
| $e_1$ | $v_1$ | $e_5$ | $e_8$ | ponecháme | ponecháme |
| $e_5$ | $p$ | $e_1$ | stejná jako pro $e_2$ | $e_3$ | stejná jako pro $e_2$ |
Veškeré informace týkající se oblastí ponecháváme beze změn. Tímto postupem dostaneme v seznamu $\mathcal D$ všechny informace o vztazích vrcholů a hran obou překryvů.
Oblasti
Každá omezená oblast je určena svou vnější hranicí představovanou vnějším cyklem. Proto k určení oblastí překryvu potřebujeme najít všechny cykly a mezi nimi určit ty, které jsou vnějšími cykly.
K určení cyklů nám stačí informace o následnících, které jsou již v seznamu $\mathcal D$ zachyceny. Vezmeme nějakou hranu $e$, najdeme jejího následníka, k němu dalšího následníka a tak dále až se dostaneme opět k hraně $e$. Potom vezmeme nějakou hranu, která v tomto cyklu nevystupuje. Stejným postupem dostaneme další cyklus. Takto tedy dostaneme všechny cykly.
Nyní si ukážeme, jak rozlišíme vnější a vnitřní cykly. V daném cyklu vezmeme vrchol $v$, který leží nejvíce vlevo (je nejmenší v lexikografickém uspořádání z 1. kapitoly). Nechť do vrcholu $v$ přichází hrana $e_1$ a vychází hrana $e_2$. Jestliže úhel od $e_1$ k $e_2$ měřený přes přilehlou oblast je menší než $180^o$, jde o cyklus vnější. Je-li tento úhel větší než $180^o$, je cyklus vnitřní.

Obrázek 3.6
Vnější cyklus $c_1$ s úhlem $\alpha\lt 180^o$, vnější cyklus $c_2$ s úhlem $\beta\gt 180^o$.
Početně o tom rozhodneme podle znaménka determinantu
$$\det \begin{pmatrix} e_{1x} \ e_{1y}\\ e_{2x} \ e_{2y} \end{pmatrix},$$kde $e_1$ a $e_2$ bereme jako vektory o souřadnicích $(e_{ix}, e_{iy})$. Je-li kladné, je cyklus vnější, je-li záporné, jde o cyklus vnitřní.
Známe tedy všechny vnější a vnitřní cykly pro překryv. Pro neomezenou oblast zaveďme ještě fiktivní cyklus $c_\infty$, který tuto oblast omezuje zvnějšku. Nyní každý vnější cyklus definuje právě jednu oblast. Abychom k oblastem přiřadili i vnitřní cykly sestrojíme následující graf $\mathcal G$. Jde o graf ve smyslu teorie grafů, jehož uzly jsou všechny cykly. Hrany tohoto grafu vytvoříme následujícím způsobem:
Vezmeme vnitřní cyklus $c_1$. Nechť $p$ je ten z jeho vrcholů, který leží nejvíce vlevo. Nechť $s$ je úsečka ležící nejblíže vlevo od $p$ (informaci o nejbližší levé úsečce pro každou událost zjišťujeme v prvém kroku algoritmu při použití zametací přímky). Úsečka $s$ určuje hranu $e$ se stejnou přilehlou oblastí jako má vnitřní cyklus $c_1$. Tato hrana pak určuje cyklus $c_2$, který může být vnitřní i vnější. Jestliže vlevo od $p$ neleží žádná úsečka, vezmeme za $c_2$ onen fiktivní vnější cyklus $c_\infty$. Cykly $c_1$ a $c_2$ spojíme v grafu $\mathcal G$ hranou.

Obrázek 3.7
V grafu $\mathcal G$ je vnitřní cyklus $c_1$ spojen hranou s vnitřním cyklem $c_2$ a ten je spojen hranou s vnějším cyklem $c_3$.
V takto sestrojeném grafu určíme komponenty souvislosti. V každé komponentě je právě jeden vnější cyklus, ten určuje jednu oblast překryvu. Tedy mezi komponentami souvislosti grafu a oblastmi je vzájemně jednoznačná korespondence. Vnitřní cykly v dané komponentě souvislosti jsou vnitřními cykly odpovídající oblasti. Se znalostí vnějšího cyklu a všech vnitřních cyklů každé oblasti teď můžeme napsat v seznamu $\mathcal D$ tabulku pro oblasti. Dále ke každé hraně najdeme cyklus, ve kterém leží, a k tomuto cyklu jeho oblast. To je přilehlá oblast k dané hraně. Tím doplníme i poslední údaj v tabulce hran.
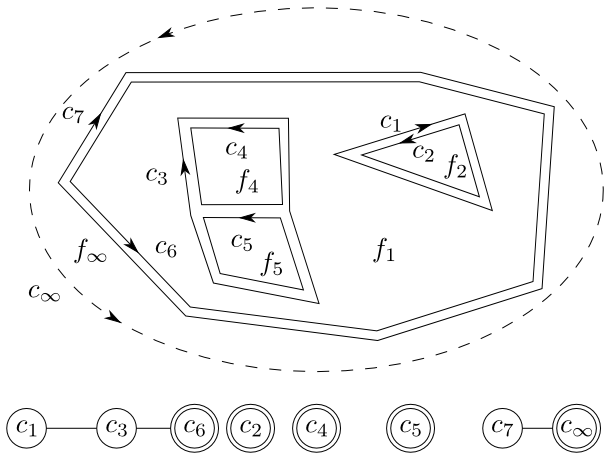
Obrázek 3.8
Cykly v rovinném podrozdělení a graf $\mathcal G$, který vytvářejí. Komponentám souvislosti grafu odpovídají postupně oblasti $f_1$, $f_2$, $f_4$, $f_5$, $f_\infty$.
Určení původních oblastí
Ještě zbývá ke každé oblasti $f$ překryvu najít oblasti $f_1$ z červené mapy a $f_2$ z modré mapy, ve kterých $f$ leží. Mohou nastat dvě možnosti. Pokud v hraničních cyklech oblasti $f$ leží hrany obou barev, pak přilehlá oblast k červené hraně je $f_1$ a přilehlá oblast k modré hraně je $f_2$, jak ukazuje následující obrázek.

Obrázek 3.9
Určení původních oblastí $f_1$ a $f_2$ pro novou oblast $f$.
Pokud jsou všechny hraniční cykly oblasti $f$ jednobarevné, řekněme červené, určíme $f_1$ stejně jako v předchozím případě. Je-li $f$ neomezená, je $f_2$ neomezená oblast v modré mapě. Pro omezenou oblast $f$ určíme oblast $f_2$ takto: vezmeme vrchol vnějšího cyklu oblasti $f$ ležící nejvíce vlevo. Najdeme k němu nejbližší úsečku vlevo. Ta určuje vnitřní nebo vnější cyklus pro oblast $f'$ sousedící s $f$. Je-li aspoň jedna hrana cyklů této oblasti modrá, určíme $f_2$ jako oblast k ní přilehlou v modré mapě. Je-li $f'$ neomezená, je oblastí $f_2$ neomezená oblast v modré mapě. Je-li $f'$ omezená a jsou-li všechny hrany jejích cyklů červené, pokračujeme stejným postupem jenom oblast $f$ teď nahradíme oblastí $f'$. Příslušná modrá oblast pro $f'$, je oblastí $f_2$ pro původní oblast $f$.

Obrázek 3.10
Určení původních oblastí $f_1$ a $f_2$ pro novou oblast $f$.
Průniky a sjednocení mnohoúhelníků
Předchozí algoritmus pro překryv map lze použít k nalezení průniku, sjednocení nebo rozdílu dvou obecně nekonvexních mnohoúhelníků. Jednoduše souvislý mnohoúhelník je takový mnohoúhelník, který je souvislý a ve svém vnitřku nemá „díry“, tj. každá uzavřená křivka lze v něm stáhnout spojitě bez přetržení do bodu. Jednoduše souvislý mnohoúhelník tedy určuje rovinné podrozdělení se dvěma oblastmi, vnitřní a vnější. Průnikem dvou mnohoúhelníků jsou ty oblasti překryvu jejich rovinných podrozdělení, které leží ve vnitřních oblastech obou podrozdělení. Podobně sjednocení mnohoúhelníků je tvořeno těmi oblastmi překryvu, které leží aspoň v jedné vnitřní oblasti odpovídajících podrozdělení. Viz následující obrázky.

Obrázek 3.11
Průnikem červeného a modrého mnohoúhelníka je sjednocení oblastí $f_2$ a $f_4$. Sjednocení mnohoúhelníků je popsáno sjednocením oblastí $f_0$ až $f_{10}$.
Pseudokódy pro algoritmu, jeho implementace a složitost
Algoritmus lze stručně shrnout takto:
Algorithm MapOverlay($S_1, S_2$)
Input. Two planar subdivisions $S_1$ and $S_2$ stored in doubly-connected edge lists.
Output. The overlay of $S_1$ and $S_2$ stored in doubly-connected edge list $\mathcal D$.
- Copy the doubly-connected edge lists for $S_1$ and $S_2$ to a new doubly-connected edge list $\mathcal D$
- Compute all intersections between edges from $S_1$ and $S_2$ with the plane sweep algorithm of Section 2.1. In addition to the actions on $\mathcal T$ and $\mathcal Q$ required at the event points, do the following:
- Update $\mathcal D$ as explained above if the event involves edges of both $S_1$ and $S_2$. (This was explained for the case where an edge of $S_1$ passes through a vertex of $S_2$)
- Store the edge immediately to the left of the event point at the vertex in $\mathcal D$ representing it.
- (* Now $\mathcal D$ is the doubly-connected edge list for $\mathcal O(S_1, S_2)$, except that the information about the faces has not been computed yet. *)
- Determine the boundary cycles in $\mathcal O(S_1, S_2)$ by traversing $\mathcal D$.
- Construct the graph $\mathcal G$ whose nodes correspond to boundary cycles and whose arcs connect each hole cycle to the cycle to the left of its leftmost vertex, and compute its connected components. (The information to determine the arcs of $\mathcal G$ has been computed in line 2, second item.)
- for each connected component in $\mathcal G$
- do Let $\mathcal C$ be the unique outer boundary cycle in the component and let $f$ denote the face bounded by the cycle. Create a face record for $f$, set OuterComponent($f$) to some edge of $\mathcal C$, and construct the list InnerComponents($f$) consisting of pointers to one edge in each hole cycle in the component. Let the InnerFace() pointers of all edges in the cycles point to the face record of $f$.
- Label each face of $\mathcal O(S_1, S_2)$ with the names of the faces of $S_1$ and $S_2$ containing it, as explained above.
Podrobné pseudokódy lze nalézt v diplomové práci Překryvy map Dominika Janků:
https://is.muni.cz/auth/th/359588/fi_m/diplomka.pdfŘádky 1 a 2 se realizují pomocí pseudokódů 4 až 10 z diplomové práce. Hledání cyklů v řádek 4 je popsán pseudokódem 13, vnitřní a vnější cykly najdeme pomocí pseudokódů 11 a 12. Komponenty souvislosti grafu $\mathcal G$ v řádku 5 se sestrojí pomocí pseudokódu 14, řádek 6 a 7 je popsán pseudokódem 16 a řádek 8 pseudokódem 15.
Součástí diplomové práce je rovněž implementace algoritmu. Její popis je v poslední kapitole práce, potřebné soubory jsou komprimovány v souboru cdrom.zip.
https://is.muni.cz/auth/th/359588/fi_m/Složitost algoritmu je charakterizována následující větou, kterou uvedeme bez důkazu.