Průnik polorovin

V této kapitole si ukážeme, jak efektivně popsat a najít průnik $n$ polorovin v rovině. Chceme postupovat rekurentně podle strategie „rozděl a panuj“. To znamená, že množinu

zadaných polorovin rozdělíme na dvě přibližně stejně velké části $H_1$ a $H_2$ a průnik

počítáme jako jako průnik $C_1\cap C_2$, kde

Zásadní roli pro postupné počítání průniků $C_1\cap C_2$ má způsob, kterým budeme průniky polorovin popisovat.

Popis průniku polorovin

Průnik polorovin je konvexní množina, která může být jak omezená, tak neomezená. Vylučme případ, že mezi polorovinami jsou dvě navzájem opačné. V tomto případě by průnik byl podmnožinou jejich společné přímky a šlo by o jednodimenzionální úlohu o průniku polopřímek na přímce.

Pokud je tedy průnik polorovin omezený a dvoudimenzionální, jde o konvexní mnohoúhelník a ten umíme popsat pomocí dvojitě souvislého seznamu s dvěma oblastmi, jednou omezenou a jednou neomezenou. Pro případ, že je průnik neomezený musíme tento popis modifikovat. Za tímto účelem použijeme lexikografické uspořádání bodů v rovině definované takto:

Uvažujme nyní neprázdnou konvexní množinu $C$, která je průnikem polorovin a přitom není podmnožinou přímky. Nastane právě jedna z následujících možností:

1. Množina C má v daném lexikografickém uspořádání maximální bod $p$ a minimální bod $q$. Oba leží na hranici a dělí ji na levou a pravou část, zkráceně na levou a pravou hranici. Každá z nich je lomená čára určená posloupností vrcholů a úseček, tyto posloupnosti budeme označovat $L(C)$ a $P(C)$.
   
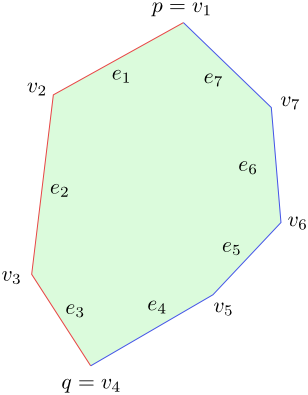
   Obrázek 5.1
   Levá hranice množiny $C$ je $L(C)=(p=v_1,e_1,v_2,e_2,v_3,e_3,q=v_4)$, pravá hranice je $P(C)=(p=v_1,e_7,v_7,e_6,v_6,e_5, v_5,e_4,q=v_4)$.
2. Množina $C$ obsahuje maximální bod $p$, ale neobsahuje minimální bod. V tomto případě dělí bod $p$ hranici množiny opět na dvě části, levou a pravou. Každá z nich je lomená čára. Určuje ji posloupností vrcholů a úseček zakončená polopřímkou.
   
   Obrázek 5.2
   Levá hranice $L(C)=(p=v_1,e_1,v_2,e_2,v_3,e_3)$, pravá hranice $P(C)=(p=v_1,e_7,v_7,e_6,v_6,e_5, v_5,e_4)$.
3. Množina $C$ obsahuje minimální bod $q$, ale neobsahuje maximální bod. V tomto případě dělí bod $q$ hranici množiny opět na dvě části, levou a pravou. Jde o lomené čáry určené posloupnostmi, které začínají polopřímkou, za kterou následují vrcholy a úsečky.
   
   Obrázek 5.3
   $L(C)=(e_1,v_2,e_2,v_3,e_3,q=v_4)$, $P(C)=(e_7,v_7,e_6,v_6,e_5, v_5,e_4,q=v_4)$.
4. Množina $C$ neobsahuje maximální bod ani minimální bod. V tomto případě má hranice levou a pravou část jenom v případě, že jde o rovnoběžné přímky. V ostatních případech má hranice pouze jedinou část, buď levou nebo pravou. Ta je určena buď jedinou přímkou nebo posloupností začínající a končící polopřímkou, mezi nimiž je posloupnost vrcholů a úseček. O druhé části hranice budeme mluvit jako o prázdné.
   
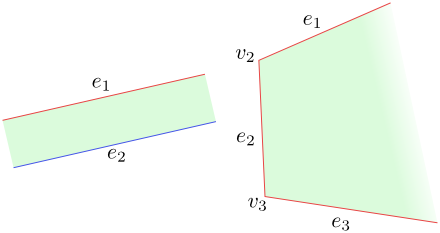
   Obrázek 5.4
   Vlevo: $L(C)=(e_1)$, $L(C)=(e_2)$. Vpravo: $L(C)=(e_1,v_2,e_2,v_3,e_3)$, $P(C)=(\ )$.

Algoritmus pro určení průniku

Nechť $C_1$ a $C_2$ jsou konvexní množiny, které vznikly jako průniky disjunkních množin polorovin. Proto jsou určeny svou levou a pravou hranicí. Popíšeme algoritmus, který z těchto čtyř posloupností vytvoří dvě posloupnosti popisující levou a pravou hranici průniku $C_1\cap C_2$.

K tomu si stačí uvědomit, že vrcholy v levé hranici $C_1\cap C_2$ jsou následující body:

• vrcholy v $L(C_1)$, které leží v $C_2$,
• vrcholy v $L(C_2)$, které leží v $C_1$,
• průsečíky levých hranic $L(C_1)$ a $L(C_2)$,
• průsečíky $L(C_1)$ a $P(C_2)$ nebo $L(C_2)$ a $P(C_1)$. Ty tvoří v daném lexikografickém uspořádání maximální nebo minimální vrchol v $L(C_1\cap C_2)$.

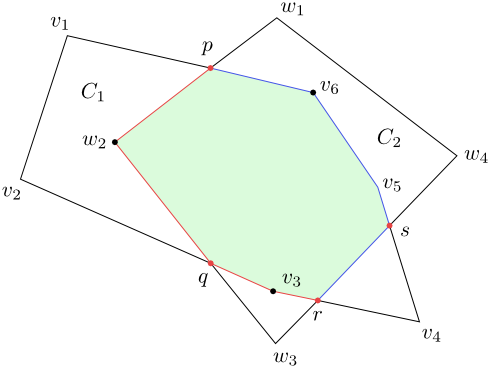
Obrázek 5.5
Vrcholy levé hranice průniku jsou $p$ – průsečík $L(C_2)$ a $P(C_1)$, $w_2\in L(C_2)$ ležící v $C_1$, $q$ – průsečík $L(C_1)$ a $L(C_2)$, $v_3\in L(C_1)$ ležící v $C_2$ a $r$ – průsečík $L(C_1)$ a 

Analogicky vrcholy v pravé hranici $C_1\cap C_2$ jsou:

• vrcholy v $P(C_1)$, které leží v $C_2$,
• vrcholy v $L(C_2)$, které leží v $C_1$,
• průsečíky pravých hranic $P(C_1)$ a $P(C_2)$,
• průsečíky $L(C_1)$ a $P(C_2)$ nebo $L(C_2)$ a $P(C_1)$. Ty jsou v daném lexikografickém uspořádání maximálním nebo minimálním vrcholem v $P(C_1\cap C_2)$.

K vytvoření seznamů $L(C_1\cap C_2)$ a $P(C_1\cap C_2)$ musíme tedy vybrat vhodné hraniční vrcholy $C_1$ a $C_2$, spočítat průsečíky hranic a vybrané vrcholy lexikograficky uspořádat. Náš algoritmus se tedy bude podobat algoritmu pro nalezení průsečíků úseček z kapitoly 1. Událostmi budou vrcholy hranic $C_1$ a $C_2$ a vypočtené průsečíky hranic. Na začátku algoritmu uspořádáme vrcholy hranic lexikograficky do fronty. Vzhledem k tomu, že v obou levých a pravých hranicích jsou vrcholy již uspořádány, tak vytvoření fronty trvá čas úměrný počtu vrcholů. Postupně budeme do fronty událostí také zařazovat vypočtené průsečíky hranic $C_1$ a $C_2$. Vzhledem k tomu, že budeme vědět, na které úsečce, resp. polopřímce, resp. přímce hranice leží, jejich zařazení do fronty bude trvat pouze konstantní čas.

V případě, že ani jedna z konvexních množin $C_1$ a $C_2$ nemá maximální bod, spočteme průniky polopřímek (přímek), kterými levé i pravé hranice obou oblastí začínají. Protože $C_1$ a $C_2$ jsou průniky disjunkních množin polorovin, tak průniky hranic budou buď prázdné konečné množiny bodů. Takto získané body zařadíme do fronty.

Zametací horizontální přímka $l$ postupuje shora dolů. Začíná v poloze nad nejvyšší událostí. U každé události ve frontě budeme evidovat, na které leží hranici a které úsečky, polopřímky nebo přímky (pro všechny tři typy objektů budeme používat společné označení hrana) jí procházejí. Rovněž budeme evidovat v jakém pořadí protínají hrany jednotlivých hranic zametací přímku. Vzhledem k tomu, že jde o pořadí nejvýše čtyř objektů, není potřeba uvažovat strom. Při průchodu přímky událostí $v$ provádíme následující akce:

• Zařadíme nebo nezařadíme událost jako vrchol do posloupnosti $L(C_1\cap C_2)$ nebo $P(C_1\cap C_2)$ podle kriterií uvedených výše.
• Je-li $v$ prvá událost zařazená do levé nebo pravé hranice průniku a vycházejí-li z ní směrem vzhůru nějaké polopřímky, rozhodneme, která z nich bude v pravé nebo levé hranici průniku.
  
  Obrázek 5.6
  Bod $v$ je prvá událost zařazená do $L(C_1\cap C_2)$. Polopřímka $f_1$ bude částí $L(C_1\cap C_2)$ nad bodem $v$, proto $L(C_1\cap C_2)=(f_1,v,\dots)$.
• Rozhodneme, která z hran vycházejících z události $v$ směrem dolů bude částí levé nebo pravé hranici průniku.
  
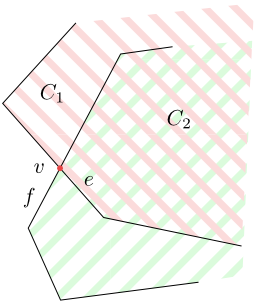
  Obrázek 5.7
  Z události $v\in L(C_1\cap C_2)$ vycházejí směrem dolů hrany $e$ a $f$. Hranu $e$ zařadíme do $L(C_1\cap C_2)$ pod událostí $v$, zatímco $f$ nikoliv.
• Vypočteme průsečík levé hrany $e_l$ vycházejících z události $v$ směrem dolů se sousední levou hranou $s_l$ hranice druhé množiny a průsečík pravé hrany $e_p$ vycházejících z události $v$ směrem dolů se sousední pravou hranou $s_p$ hranice druhé množiny. Pokud průsečíky existují, zařadíme je do fronty.
  
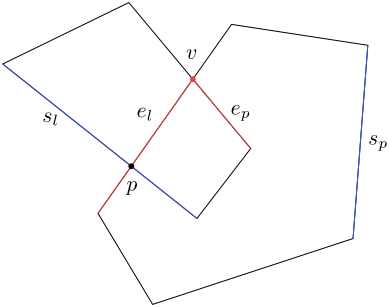
  Obrázek 5.8
  Událost $v$ a k ní příslušné hrany $e_l$, $e_p$, $s_l$, $s_p$. Průsečík $p=e_l\cap s_l$ zařadíme do fronty. Průnik $e_p\cap s_p$ je prázdný.
• Jestliže najdeme událost, která bude minimálním vrcholem levé i pravé hranice průniku, vyjmeme z fronty všechny události, neboť popis levé a pravé hranice průniku je již úplný. V opačném případě vyjmeme z fronty pouze událost $v$.

Algoritmus končí v okamžiku, kdy je fronta událostí prázdná.

Pseudokódy a jejich časová náročnost

Průnik dvou konvexních množin získáme takto:

Průchod zametací přímky přes událost $v$ zachycuje následující pseudód:

Časová náročnost posledního pseudokódu je konstantní. Nechť konvexní množiny $C_1$ a $C_2$ jsou popsány $n_1$ a $n_2$ vrcholy. Potom časová náročnost pseudokódu IntersectionOfTwo($C_1,C_2$) je $O(n_1+n_2)$.

Časová náročnost $T(n)$ celého algoritmu pro výpočet průniku $n$ polorovin je dána rekurentně vztahem

Ten vede k výsledné časové náročnosti

Animace

Výpočet průniku dvou konvexních množin $C_1$ a $C_2$ podle druhého a třetího algoritmu je zachycen v následující animaci.