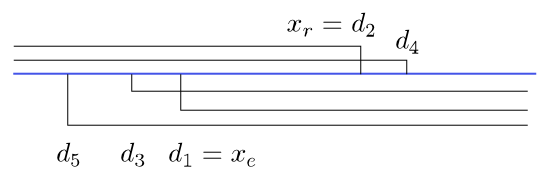Úloha lineárního programování v rovině
Úvod
Pro zadanou lineární funkci $f:\mathbb R^2\to \mathbb R$:
$$f(x,y)=c_1x+c_2y,\qquad (c_1,c_2)\ne (0,0),$$
a množinu $n$ polorovin $H = \{h_1, h_2, \dots, h_n\}$ chceme
najít bod v průniku těchto polorovin
$$(x,y)\in h_1\cap h_2\cap\dots\cap h_n=\bigcap_{i=1}^{n}h_i=\bigcap H,$$
v němž funkce $f$ nabývá svého maxima. Body polorovin $h_i$ přitom
splňují nerovnosti
\begin{equation}\label{polorovina}
a_{i1}x+a_{i2}y\le b_i.
\end{equation}
Jaký je geometrický význam této úlohy? Funkce $f$ je určena vektorem
$\vec{c}=(c_1,c_2)$. Stejné hodnoty $k\in \mathbb R$ nabývá funkce $f$ na přímce
$$\{(x,y)\in \mathbb R^2; c_1x+c_2y=k\}.$$
Přitom vektor $c$ je kolmý na všechny takové přímky. Tedy $f$ se mění
ve směru vektoru $\vec{c}$. Protože $f(c_1,c_2)=c_1^2+c_2^2>0$, tak funkce $f$ ve
směru vektoru $\vec{c}$ roste. Nabývá-li tedy funkce $f$ na průniku polorovin
svého maxima, pak je to v bodě, který je „nejvzdálenějším“ bodem průniku ve
směru vektoru $\vec{c}$.
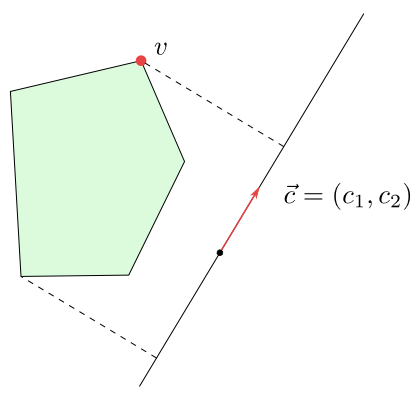
Obrázek 6.1
Bod $v$ je bodem, kde $f$ nabývá svého maxima na daném pětiúhelníku.
Jak je to s řešitelností naší úlohy? Mohou nastat tyto možnosti:
- Průnik polorovin je prázdný.
- Existuje jediný bod, v němž $f$ nabývá svého maxima.
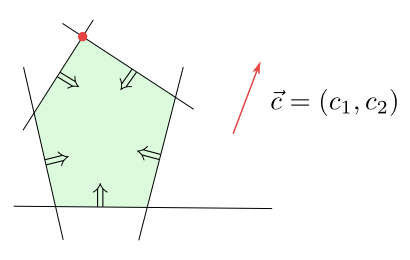
Obrázek 6.2
- Existuje nekonečně mnoho bodů, v nichž $f$ nabývá svého maxima.
Tyto body tvoří úsečku, polopřímku nebo přímku.
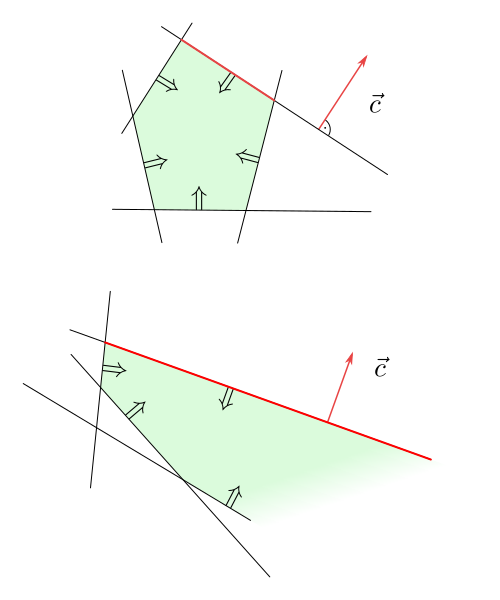
Obrázek 6.3
- Funkce $f$ je na průniku polorovin shora neomezená. V tomto případě existuje
v průniku polorovin polopřímka a $f$ podél ní roste.
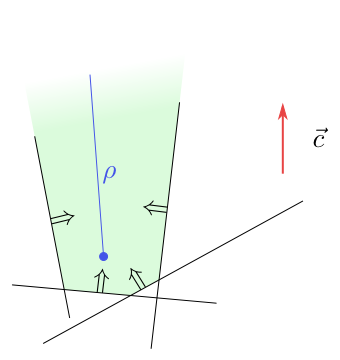
Obrázek 6.4
Funkce $f$ je na polopřímce $\rho$ shora neomezená.
Vstupem našeho algoritmu bude tedy nenulový vektor $\vec{c}$ a poloroviny
$h_1,h_2,\dots,h_n$ zadané nerovnostmi (\ref{polorovina}). Výstupem bude
jedna z následujících možností:
- Informace, že průnik polorovin je prázdný, společně se
třemi polorovinami $h_i$, $h_j$, $h_k$ takovými, že
$$h_i\cap h_j\cap h_k=\emptyset.$$
- Jeden bod, v němž $f$ nabývá svého maxima.
- Informace, že $f$ nenabývá v průniku svého maxima, společně s rovnicí
polopřímky, která leží v průniku polorovin a podél níž funkce $f$ roste.
Jednodimenzionální úloha lineárního programování
Úlohu
lineárního programování můžeme formulovat v libovolné dimenzi. V dimenzi 1
je řešení této úlohy obzvláště jednoduché a náš algoritmus pro řešení
dvoudimenzionální úlohy bude řešení jednodimenzionální úlohy používat v několika krocích.
V jednodimenzionální úloze jde o to najít $x\in \mathbb R$, v němž funkce
$$f(x)=cx,\qquad c\ne 0,$$
nabývá svého maxima za podmínek
$$a_ix\le b_i, \qquad a_i\ne 0,$$
pro $i=1,2,\dots,n$. Nechť $I=\{i;a_i>0\}$ a $J=\{j;a_j\lt0\}$. Pak po dělení
čísly $a_i$ dostaneme
\begin{align*}
x&\le \frac{b_i}{a_i}=d_i\quad \text{pro} i\in I,\\
x&\ge \frac{b_j}{a_j}=d_j\quad \text{pro} j\in J.
\end{align*}
Položme
$$x_l=\max\{d_j,-\infty;j\in J\} \quad \text{a}\quad
x_r=\min\{d_i,\infty;i\in I\}.$$
Mohou nastat tyto možnosti:
- $x_r\lt x_l$. Pak je průnik polopřímek určených nerovnostmi prázdný.
- $x_l\le x_r<\infty$ a $c>0$. V tomto případě nabývá $f$ svého maxima
v $x_r$.
- $-\infty\lt x_l\le x_r$ a $c\lt0$. V tomto případě nabývá $f$ svého maxima
v $x_l$.
- Pokud $x_r=\infty$ a $c>0$ nebo $x_l=-\infty$ a $c\lt0$, pak průnik
polopřímek je polopřímka, na které funkce $f$ roste.
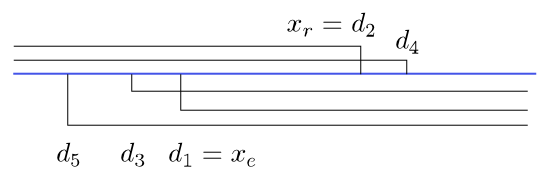
Obrázek 6.5
Určení $x_l$ a $x_r$ pro $I=\{2,4\}$ a $J=\{1,3,5\}$.
Z předchozího postupu je vidět, že řešit jednodimenzionální úlohu
lineárního programování s $n$ nerovnostmi spočívá v nalezení maxima a minima
z množiny čísel, která má maximálně $n$ prvků. Časová náročnost takového
algoritmu je tedy $O(n)$.
Omezená úloha lineárního programování v rovině
Nejprve si
ukážeme, jak řešit úlohu lineárního programování v rovině v případě, že
máme zaručeno, že funkce $f$ je na průniku polorovin omezená.
Předpokládejme, že mezi polorovinami $h_i$ jsou dvě, označme je $h_1$ a $h_2$, takové, že $f$ je omezená na $h_1\cap h_2$. Navíc předpokládejme,
že průnikem není polorovina. Potom $f$ nabývá svého maxima na $h_1\cap h_2$
určitě v průsečíku $v_2$ hraničních přímek $l_1\cap l_2$. To je buď jediný bod
maxima, nebo, pokud je bodů maxima více, je minimální či
maximální v lexikografickém uspořádání – viz obrázek 6.6. Pro další úvahy
budeme předpokládat, že $v_2$ je z těch bodů, v nichž $f$ dosahuje svého
maxima, v lexikografickém uspořádání minimální.
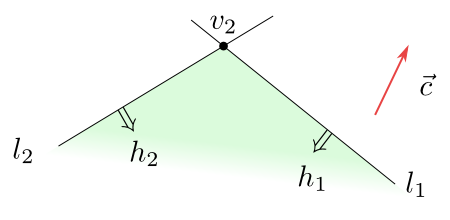
Obrázek 6.6
Funkce $f$ je omezená na $h_1\cap h_2$. Svého maxima nabývá v bodě $v_2$.
Bod
maxima funkce $f$ na $C_2=h_1\cap h_2$ známe a chceme najít
postupně body
$$v_i\in C_i=h_1\cap h_2\cap h_3\cap \dots \cap h_i$$
tak, že (pokud je $C_i$ neprázdná)
- funkce $f$ nabývá v bodě $v_i$ svého maxima na množině $C_i$,
- z bodů, v nichž $f$ nabývá svého maxima, je $v_i$ minimální v lexikografickém uspořádání.
Následující věta říká, jak najdeme $v_i$, známe-li $v_{i-1}$.
Věta 6.1
Je-li $v_{i-1}\in h_i$, pak $v_i=v_{i-1}$.
Jestliže $v_{i-1}\notin h_i$, pak buď $C_i=\emptyset$ nebo $v_i$ leží na
hraniční přímce $l_i$ poloroviny $h_i$. V tomto případě najdeme $v_i$
řešením úlohy jednodimenzionálního lineárního programování. V případě, že průnik polopřímek
při řešení jednodimenzionální úlohy je prázdný, dostaneme poloroviny $h_k$, $h_j$ s $k,j\lt i$ takové, že $h_k\cap h_j\cap h_i=\emptyset$.
Důkaz
Platí, že $C_i\subseteq C_{i-1}$. Je-li $v_{i-1}\in h_i$, je $v_{i-1}\in
C_i$ a protože je bodem maxima funkce $f$ na $C_{i-1}$, musí být bodem
maxima funkce $f$ i na $C_i$. Protože je z bodů maxima na $C_{i-1}$
minimální, podrží si tuto vlastnost i na $C_i$.
Nechť nyní $v_{i-1}\notin h_i$. Předpokládejme, že $v_i\in h_i$, ale neleží
na hraniční přímce $l_i$. Spojme body $v_{i-1}$ a $v_i$ úsečkou. Ta musí
protínat přímku $l_i$. Jejich průsečík označme $q$, viz obrázek 6.7. Platí
$$f(v_{i-1})\ge f(v_i).$$
Funkce $f$ je lineární na úsečce $[v_{i-1},v_i]$.
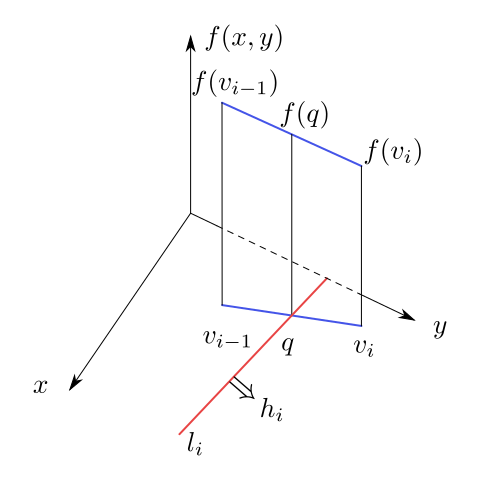
Obrázek 6.7
Funkce $f$ je lineární na úsečce $[v_{i-1},v_i]$.
Jestliže tedy
$f(v_{i-1})>f(v_i)$, pak musí platit
$$f(v_{i-1})>f(q)>f(v_i).$$
Protože $q\in C_i$, dostáváme spor s tím, že $v_i$ je bodem maxima funkce
$f$ na $C_i$.
Jestliže $f(v_{i-1})=f(v_i)$, pak $f(v_{i-1})=f(q)$. V tomto případě musí být
v lexikografickém uspořádání $v_{i-1}\lt q$, neboť $v_{i-1}$ je z bodů, kde $f$ nabývá svého maxima na $C_{i-1}$, minimální v lexikografickém uspořádání. A protože body na úsečce jsou
uspořádány lexikograficky lineárně, je také
$$v_{i-1}\lt q\lt v_i,$$
což je opět spor s definicí $v_i$ jako bodu maxima funkce $f$ na $C_i$
minimálního v lexikografickém uspořádání.
Tím jsme dokázali, že $v_i$ musí ležet na přímce $l_i$. Ukážeme si, jak jej
najdeme. Nechť souřadnice bodu $v_i$ jsou $(x,y)$. Protože leží na přímce
$l_i$ splňují rovnici $a_{i1}x+a_{i2}y=b_i$. Předpokládejme, že $a_{i2}\ne
0$. Pak můžeme spočítat $y$ pomocí $x$
$$y=\frac{b_i-a_{i1}x}{a_{i2}}.$$
Hledáme maximum funkce $f$ na $l_i$. Tuto funkci lze považovat za funkci
jedné proměnné
$$g(x)=c_1x+c_2\left(\frac{b_i-a_{i1}x}{a_{i2}}\right)=
\left(c_1-c_2\frac{a_{i1}}{a_{i2}}\right)x
-c_2\frac{b_i}{a_{i2}}.$$
Bod maxima lineární funkce $g$ nezávisí na konstantě, proto je stejný jako
bod maxima funkce
$$\widetilde g(x)=\left(c_1-c_2\frac{a_{i1}}{a_{i2}}\right)x=cx.$$
Její maximum hledáme na množině
$C_{i-1}\cap l_i$, která je popsána nerovnostmi
$$a_{j1}x+a_{j2}\left(\frac{b_i-a_{i1}x}{a_{i2}}\right)\le b_j$$
pro $j=1,2,\dots,i-1$. Ty lze upravit na nerovnosti
$$\left(a_{j1}-a_{j2}\frac{a_{i1}}{a_{i2}}\right)x\le b_j-a_{j2}
\frac{b_i}{a_{i2}}.$$
Je tedy vidět, že nalezení souřadnic bodu $v_i$ nebo zjištění, že $C_i$ je
prázdné v případě $v_{i-1}\notin h_i$, je řešením jednodimenzionální úlohy
lineárního programování.
\(\Box\)
Časová náročnost algoritmu pro omezenou úlohu lineárního programování
Předchozí věta určuje algoritmus pro řešení omezené úlohy
lineárního programování. Ten je níže popsán v pseudokódu 2dRandomizedLP v řádcích 10–17.
Časová náročnost nalezení $v_i$ je konstantní, jestliže $v_{i-1}\in h_i$,
a lineární $O(i)$, jestliže $v_{i-1}\notin h_i$. Protože řešením úlohy je
nalezení bodu $v_n$, je celková časová náročnost nejvýše rovna
$$O(3)+O(4)+\dots +O(n)=O(3+4+\dots +n)=O(n^2).$$
Tato časová náročnost je příliš vysoká. Ve skutečnosti záleží na tom, v jakém pořadí bereme pro výpočet $v_3, v_4, \dots, v_n$ poloroviny
$h_3,h_4,\dots,h_n$. Ukažme si to na příkladu z obrázků 6.8 a 6.9.
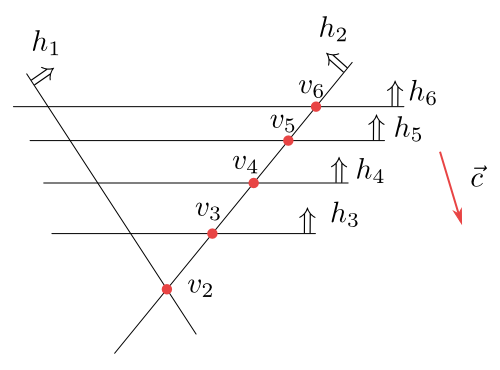
Obrázek 6.8
V této situaci máme pořadí polorovin $h_3,h_4,h_5,h_6$ a navzájem různé
body $v_2$, $v_3$, $v_4$, $v_5$, $v_6$. Přitom jsme všechny s výjimkou prvého museli
počítat pomocí 1-dimenzionální úlohy lineárního programování.
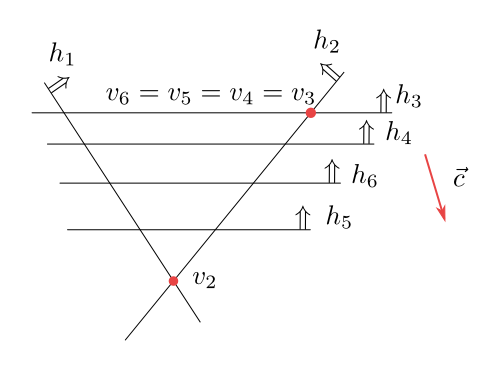
Obrázek 6.9
Tento obrázek zachycuje stejnou situaci, jenom jednotlivé poloroviny jsou
očíslovány tak, že $v_3=v_4=v_5=v_6$ Tedy pouze $v_3$ jsme museli počítat
pomocí 1-dimenzionální úlohy lineárního programování.
Náhodnostní algoritmus
Uvažujme všechna možná pořadí polorovin $h_3, h_4, \dots, h_n$. Z předchozího příkladu je vidět, že pro různá pořadí dostaneme v konkrétním případě různou časovou náročnost výpočtu. Očekávaná časová náročnost (expected randomized time) je průměrná doba výpočtu. V případě lineárního programování v rovině bude daleko příznivější než $O(n^2)$. Vezmeme-li tedy pořadí polorovin $h_3, h_4, \dots, h_n$ náhodně lze očekávat, že reálná doba výpočtu se bude shodovat s očekávanou časovou náročností. Tyto úvahy vedou k tzv. náhodnostnímu algoritmu. Náhodné pořadí polorovin
lze realizovat podle následujícího algoritmu:
Algorithm RandomPermutation(A)
Input. An array $A[1\ldots n]$.
Output. The array $A[1\ldots n]$ with the same elements, but rearranged into a random permutation.
- for $k\leftarrow n$ downto $2$
- do rndindex$\leftarrow$Random$(k)$
- Exchange $A[k]$ and $A[$rndindex$]$.
kde procedura RANDOM($k$) generuje v konstantním čase náhodné přirozené číslo mezi $1$ a $k$.
Cílem tohoto paragrafu je ukázat, že platí
Věta 6.2
Očekávaná časová náročnost popsaného algoritmu pro řešení
$2$-dimenzionální úlohy lineárního programování pro $n$ polorovin je $O(n)$.
Důkaz
Všimněte si, že tvrzení je formulováno i pro neomezenou úlohu. Důkaz provedeme pouze
pro omezenou úlohu. Jeho doplnění pro neomezenou úlohu je totiž jednoduché.
Nechť $X_i$ je náhodná veličina definovaná takto:
\begin{equation*}
X_i =
\begin{cases}
1, &\text{je-li $v_{i-1}\notin h_i$,}\\
0, &\text{je-li $ v_{i-1}\in h_i$.}
\end{cases}
\end{equation*}
Čas potřebný k provedení algoritmu je potom shora odhadnut náhodnou veličinou
$$\sum_{i=3}^n O(i) X_i.$$
Očekávaná časová náročnost pak bude střední hodnotou této náhodné veličiny
$$E\left(\sum_{i=3}^n O(i) X_i\right)=\sum_{i=3}^n O(i)E(X_i).$$
Střední hodnotu náhodné veličiny $X_i$, která nabývá hodnot $0$ a $1$ spočítáme takto:
\begin{align*}
E(X_i)&=0\cdot \text{pravděpodobnost}\{X_i=0\}+1\cdot \text{pravděpodobnost}\{X_i=1\}\\
&=\text{pravděpodobnost}\{X_i=1\}.
\end{align*}
Stačí tedy spočítat pravděpodobnost, že $v_{i-1}\notin h_i$. Provedeme tzv. zpětnou analýzu.
Bod $v_i\in C_i$ leží vždy na průsečíku dvou přímek $l_j$ a $l_k$ ohraničujících poloroviny
$h_j$ a $h_k$ pro $j,k\leq i$ a $j,k$ minimální s touto vlastností. Pravděpodobnost, že $v_{i-1}\notin h_i$ je stejná jako pravděpodobnost, že $j=i$ nebo $k=i$, a ta je
$\frac{2}{i}$. Tedy
$$ E\left(\sum_{i=3}^n O(i) X_i\right)=\sum_{i=3}^n O(i) \frac{2}{i}=\sum_{i=3}^n O(1)=O(n).$$
\(\Box\)
Neomezená úloha lineárního programování
Pro řešení obecné úlohy lineárního programování musíme nejdříve zjistit, zda je funkce $f$ na průniku polorovin vůbec omezená.
Dokladem pro neomezenost $f$ je existence polopřímky
$$\rho=\{p+\lambda \vec{d}, \lambda\geq 0\}$$
v průniku polorovin, na které $f$ roste s rostoucím $\lambda$. Zde je $p$ bod v průniku polorovin a $\vec{d}$ je vhodný vektor.
Nutná a postačující podmínka pro to, aby $f$ byla na $\rho$ neomezená, je, že úhel mezi vektory $\vec{c}$ a $\vec{d}$ je ostrý, tj. že skalární součin $\langle \vec{d}, \vec{c}\rangle>0$. (Připomeňme, že $f$ roste ve směru vektoru $\vec{c}$.)
Nutná podmínka pro to, aby polopřímka $\rho$ ležela v polorovině $h_i$, je dána tím, že vektor $\vec{d}$ nesmí s vnitřním normálovým vektorem $\vec{\eta_i}$ poloroviny $h_i$ svírat tupý úhel, tj.
skalární součin $\langle \vec{d},\vec{\eta_i}\rangle\geq 0$. Jestliže $\vec{d}$ svírá s $\vec{\eta_i}$ tupý úhel, pak každá polopřímka se směrovým vektorem $\vec{d}$ polorovinu $h_i$ dříve nebo později opustí, viz obrázek.
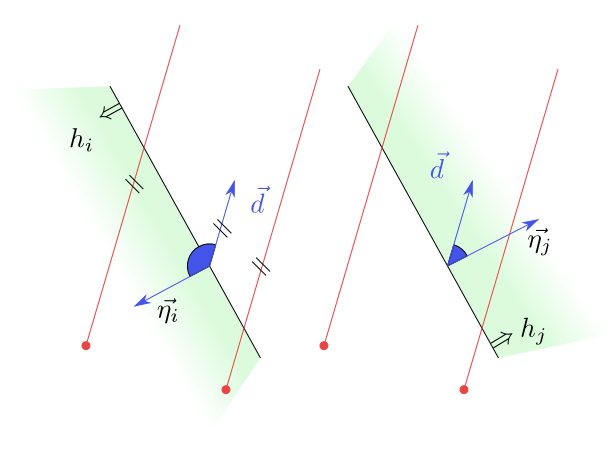
Obrázek 6.10
Je-li $\langle \vec{d},\vec{\eta_i}\rangle\lt 0$, pak polorovina $h_i$ neobsahuje polopřímku se směrovým vektorem $\vec{d}$. Je-li $\langle \vec{d},\vec{\eta_j}\rangle\geq 0$,
pak $h_j$ takové polopřímky obsahuje.
Důležitou roli, hrají také poloroviny, jejichž hranice je rovnoběžná s vektorem $\vec{d}$, tj. ty, pro které
je $\langle \vec{d},\vec{\eta_i}\rangle=0$. Polopřímka $\rho$ musí ležet v jejich průniku, tedy speciálně, tento průnik musí být neprázdný.
Úlohu lineárního programování budeme zkráceně nazývat lineární program a označovat $LP(H,\vec{c})$, kde $H$ označuje množinu polorovin a $\vec{c}$ definuje funkci $f$ na vstupu. Řekneme, že lineární program je neomezený, jestliže v průniku polorovin existuje polopřímka $\rho$, na které $f$ roste. Předchozí úvahy vedou k následujícímu tvrzení:
Věta 6.3
$LP(H,\vec{c})$ je neomezený, právě když existuje vektor $\vec{d}$ tak, že platí
\begin{equation}\label{d}
\langle \vec{d},\vec{c}\rangle>0,\quad \text{a}\quad \langle \vec{d},\vec{\eta_i}\rangle\geq 0
\quad\text{pro}1\leq i\leq n,
\end{equation}
a poloroviny z množiny $H'=\{h_i\in H; \langle \vec{d},\vec{\eta_i}\rangle=0\} $ mají neprázdný průnik.
Podstatné pro nás je jak najít vektor $\vec{d}$ algoritmicky.
Věta 6.4
Vektor $\vec{d}$ z předchozí věty lze najít řešením $1$-dimenzionální úlohy lineárního programování,
o neprázdnosti průniku polorovin z $H'$ lze rozhodnout rovněž řešením
$1$-dimenzionální úlohy lineárního programování.
Jestliže vektor $\vec{d}$ splňující (\ref{d}) neexistuje, dá nám $1$-dimenzionální úloha dvě roviny $h_j$ a $h_k$, že $f$ je omezená na
$h_j\cap h_k$. Jestliže $\vec{d}$ existuje, ale průnik polorovin z $H'$ je prázdný, dá nám $1$-dimenzionální algoritmus pro hledání tohoto průniku dvě poloroviny z $H'$, jejichž průnik je prázdný.
Důkaz
Jestliže vektor $\vec{d}$ splňuje podmínky věty 6.3, pak je splňuje každý jeho kladný násobek. Hledejme tedy $\vec{d}$ ve tvaru
$$\vec{d}=\vec{c}+t\vec{e},$$
kde $\vec{e}$ je pevný jednotkový vektor kolmý k $\vec{c}$. Pak
$$\langle \vec{d},\vec{c}\rangle=\langle \vec{c}+t\vec{e},\vec{c}\rangle=\langle \vec{c},\vec{c}\rangle>0$$
a stačí najít reálné číslo $t$ tak, aby
$$\langle \vec{c}+t\vec{e},\vec{\eta_i}\rangle\geq 0 \quad\text{pro všechna $i$}.$$
To vede k hledání $t\in \mathbb R$, které splňuje nerovnosti
$$t\langle \vec{e},\vec{\eta_i}\rangle \geq -\langle \vec{c},\vec{\eta_i}\rangle\quad\text{pro všechna $i$},$$
což je $1$-dimenzionální úloha lineárního programování. Jestliže tato úloha nemá řešení, je to proto, že soustava pouze dvou nerovností pro nějaké $j$ a $k$ nemá řešení. Tedy $f$ bude omezená na průniku $h_j\cap h_k$.
Existuje-li $\vec{d}$ splňující nerovnosti z věty 6.3, určíme množinu $H'$. Vezměme přímku
$L=\{(x,y), \langle(x,y),\vec{d}\rangle=0\}$. Ta je kolmá k hraničním přímkám všech polorovin $h_i$ z $H'$. Průnik polorovin z $H'$ je neprázdný, právě když je neprázdný průnik polopřímek
$$\cap_{h_i\in H'}(L\cap h_i).$$
To je opět úloha $1$-dimenzionálního lineárního programování. Je-li průnik prázdný, dostaneme dvě poloroviny, jejichž průnik je prázdný. To pak vede k závěru, že průnik všech polorovin z $H$ je prázdný.
\(\Box\)
Celý algoritmus, jehož detaily jsme vysvětlili, je nyní zachycen v následujícím pseudokódu
Algorithm 2DRandomizedLP($H,\vec{c}$)
Input. A linear program ($H,\vec{c}$), where $H$ is a set of $n$ half-planes and $\vec{c}\in\mathbb R^2$.
Output. If ($H,\vec{c}$) is unbounded, a ray is reported. If it is infeasible, then two or three certificate half-planes are reported. Otherwise, the lexicographically smallest point $p$ that maximizes $f_{\vec{c}}(p)$ is reported.
- Determine whether there is a direction vector $\vec{d}$ such that $\vec{d}\cdot\vec{c}\gt 0$ and $\vec{d}\cdot\vec{\eta}(h)\ge 0$ for all $h\in H$
- if $\vec{d}$ exists
- then compute $H^{'}$ and determine whether $H^{'}$ is feasible.
- if $H^{'}$ is feasible
- then Report a ray proving that ($H,\vec{c}$) is unbounded and quit.
- else Report that ($H,\vec{c}$) is infeasible and quit.
- Let $h_1, h_2\in H$ be certificates proving that ($H,\vec{c}$) is bounded and has a unique lexicographically smallest solution.
- Let $v_2$ be the intersection of $l_1$ and $l_2$.
- Let $h_3, h_4,\ldots, h_n$ be a random permutation of the remainning half-planes in $H$.
- for $i\leftarrow 3$ to $n$
- do if $v_{i-1}\in h_i$
- then $v_i\leftarrow v_{i-1}$
else $v_i\leftarrow$the point $p$ on $l_i$ that maximizes $f_{\vec{c}}(p)$, subject to the constraints in $H_{i-1}$.
- if $p$ does not exist
then Let $h_j, h_k$ (with $j,k\lt i$) be the certificates (possibly $h_j=h_k$) with $h_j\cap h_k\cap l_i =\emptyset$.
Report that the linear program is infeasible, with $h_i, h_j, h_k$ as certificates, and quit.
- return $v_n$
Detailní popis algoritmu včetně implementace lze najít v bakalářské práci Jana Kováře
na webové stránce
https://is.muni.cz/auth/th/323609/prif_b/?lang=cs