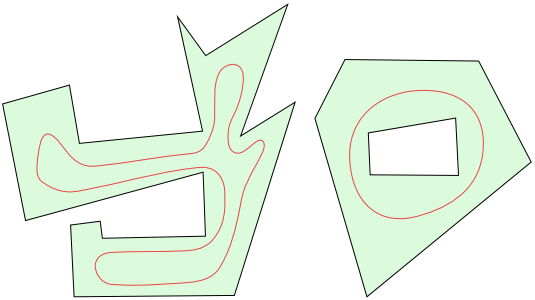Triangulace mnohoúhelníka
Úvod
V této kapitole si ukážeme, jak daný jednoduchý mnohoúhelník rozdělit na trojúhelníky s vrcholy ve vrcholech tohoto mnohoúhelníka. Připomeňme si, že v jednoduchém mnohoúhelníku lze každou uzavřenou křivku stáhnout spojitě do jediného bodu. To znamená, že v něm nejsou žádné „díry“ a že má pouze vnější hranici tvořenou jedinou lomenou čarou.
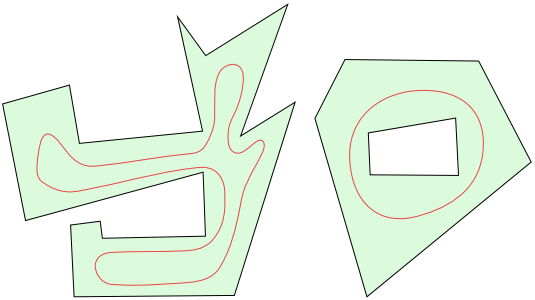
Obrázek 4.1
Jednoduchý a nejednoduchý lichoběžník.
Vstupem našeho algoritmu bude dvojitě souvislý seznam pro rovinné podrozdělení určené mnohoúhelníkem a výstupem bude dvojitě souvislý seznam pro rovinné podrozdělení dané triangulací mnohoúhelníka.
Obrázek 4.2
Ukázka triangulace.
Podíváte-li se na předchozí obrázek a spočítáte-li si počet trojúhelníků, na které jsme daný
17-úhelník rozdělili, tak vás následující tvrzení nepřekvapí:
Věta 4.1
Každý jednoduchý $n$-úhelník lze triangulovat. Každá jeho triangulace se skládá z $n-2$ trojúhelníků.
Důkaz
Budeme postupovat indukcí podle $n$. Pro $n=3$ jsou obě tvrzení evidentní. Předpokládejme, že jsou pravdivá pro všechny $k$-úhelníky s $3\leq k\lt n$ a uvažujme libovolný $n$-úhelník $P$.
Prvně ukážeme, že ho lze triangulovat.
Vezměme jeho vrchol $v$, který je nejmenší v lexikografickém uspořádání nejdřív podle souřadnice $x$ a potom podle $y$. (Leží ze všech vrcholů nejvíce vlevo, a pokud je takových více, tak nejvíce dole.) Z tohoto vrcholu vedou strany do vrcholů $u$ a $w$. Jestliže úsečka $uw$ leží v $P$, můžeme vytvořit v $P$ trojúhelník $uvw$ a tím se $P$ rozpadne na tento trojúhelník a na $(n-1)$-úhelník $Q$. Ten lze triangulovat podle indukčního předpokladu.
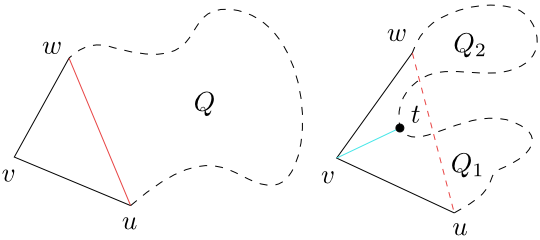
Obrázek 4.3
K důkazu věty 4.1.
Jestliže úsečka $uw$ neleží celá v $P$, musí v trojúhelníku $uvw$ ležet ještě nějaké další vrcholy mnohoúhelníka $P$. Z nich vybereme vrchol $t$ nejdále od úsečky $uw$. Potom úsečka $vt$ leží celá v mnohoúhelníku $P$. (Kdyby tomu tak nebylo, musela by ji protínat nějaká strana a jeden z jejích vrcholů by ležel od $uw$ dále než vrchol $t$.) Tedy spojnice $vt$ rozděluje
$n$-úhelník na dva jednoduché mnohoúhelníky $Q_1$ a $Q_2$ se společnou stranou $tv$, které lze triangulovat. Jejich triangulace dává triangulaci mnohoúhelníka $P$.
Nyní uvažujme libovolnou triangulaci $n$-úhelníka $P$. Pokud je $n\gt 3$, pak některá strana trojúhelníka v této triangulaci není stranou mnohoúhelníka a tedy rozděluje $n$-úhelník $P$
na dva jednoduché triangulované mnohoúhelníky $Q_1$ a $Q_2$ se společnou stranou, které mají postupně
$n_1$ a $n_2$ vrcholů. Proto $n_1+n_2=n+2$. Použijeme-li na $Q_1$ a $Q_2$ indukční předpoklad, je celkový počet trojúhelníků v triangulaci mnohoúhelníka $P$ roven
$$(n_1-2)+(n_2-2)=(n_1+n_2)-4=(n+2)-4=n-2.$$
\(\Box\)
Monotónní mnohoúhelníky
Triangulace konvexního mnohoúhelníku je velice jednoduchá. Jedna z více možností je, že vezmeme nějaký vrchol a spojíme ho se všemi nesousedními vrcholy.
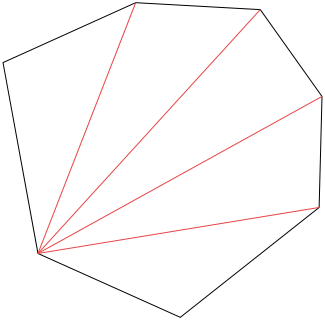
Obrázek 4.4
Triangulace konvexního mnohoúhelníku.
Požadavek konvexnosti můžeme oslabit. Můžeme požadovat, aby každá přímka rovnoběžná s osou $x$ (tedy daná rovnicí $y=k$) protínala mnohoúhelník v konvexní množině, tj. v úsečce, bodě nebo prázdné množině. Takový mnohoúhelník budeme nazývat monotónní vzhledem k ose $y$.
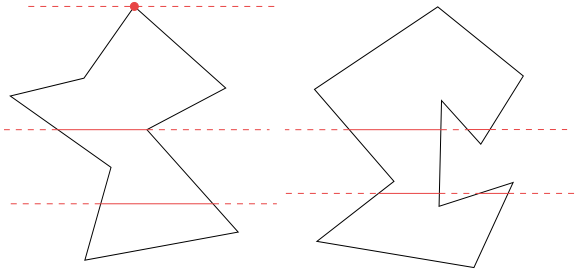
Obrázek 4.5
Monotónní a nemonotónní mnohoúhelnik.
Tato definice je geometricky názorná, ale pro naše potřeby vyžaduje zpřesnit. Uvažujme lexikografické uspořádání používané pro metodu zametací přímky:
$$p\gt q\ \text{právě když}\ p_y\gt q_y\ \text{nebo}\ p_y=q_y\ \text{a}\ p_x\lt q_x.$$
Označme vrchol mnohoúhelníka maximální v tomto uspořádání jako $u$ a minimální vrchol jako
$d$. Tyto body dělí hranici mnohoúhelníka na dvě části – levou a pravou. Budeme mluvit o levé cestě a pravé cestě od $u$ k $d$. Zpřesnění definice mnohoúhelníka monotónního vzhledem k ose $y$ spočívá v tom, že požadujeme, aby obě cesty od $u$ k $d$ klesaly v popsaném lexikografickém uspořádání. Mnohoúhelník monotónní podle této definice je určitě monotónní podle předchozí geometrické definice. Opačně to neplatí, jak ukazuje následující obrázek.
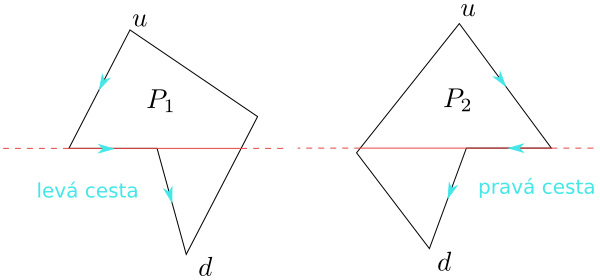
Obrázek 4.6
Podle geometrické definice jsou oba mnohoúhelníky monotónní. Podle zpřesněné definice je monotónní pouze $P_1$. Pravá cesta mnohoúhelníku $P_2$ není klesající.
Ukazuje se, že monotónní mnohoúhelníky lze relativně dobře triangulovat. Proto rozdělíme algoritmus pro triangulaci jednoduchého mnohoúhelníka na dvě části:
- rozdělení mnohoúhelníka na monotónní mnohoúhelníky,
- triangulace monotónních mnohoúhelníků.
Typy vrcholů mnohoúhelníka a jeho monotónnost
Nechť $v$ je vrchol mnohoúhelníka a $p$ a $n$ jsou jeho sousední vrcholy. Vrchol $v$ je právě jedním z následujících typů:
Start – jestliže cesta z $p$ do $v$ je rostoucí v uvažovaném lexikografickém uspořádání, cesta z $v$ do $n$ je klesající a mnohoúhelník $P$ sousedí s vrcholem $v$ zdola.
End – jestliže cesta z $p$ do $v$ je klesající, cesta z $v$ do $n$ je rostoucí a mnohoúhelník $P$ sousedí s vrcholem $v$ shora.
Split – jestliže cesta z $p$ do $v$ je rostoucí, cesta z $v$ do $n$ je klesající a mnohoúhelník $P$ sousedí s vrcholem $v$ shora.
Merge – jestliže cesta z $p$ do $v$ je klesající, cesta z $v$ do $n$ je rostoucí a mnohoúhelník $P$ sousedí s vrcholem $v$ zdola.
Regular – jestliže cesta z $p$ přes $v$ do $n$ je buď rostoucí nebo klesající.
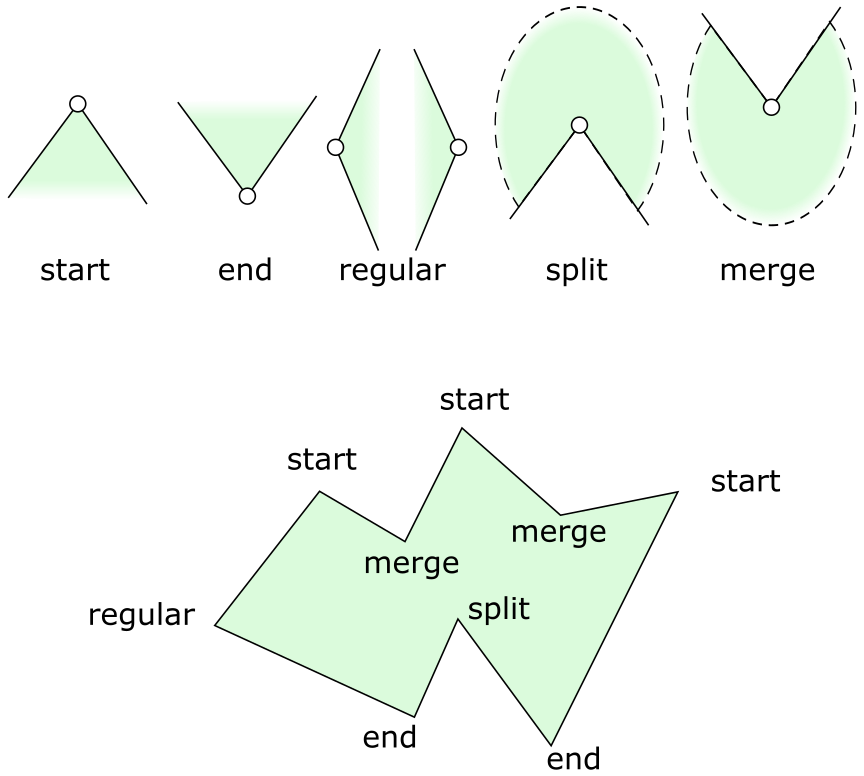
Obrázek 4.7
Typy vrcholů.
Algoritmus pro rozdělení mnohoúhelníka na monotónní části je založen na tvrzení:
Věta 4.2
Jednoduchý mnohoúhelník je monotónní vzhledem k ose $y$, právě když nemá vrcholy typu split a merge.
Důkaz
Z definic je zřejmé, že pokud má mnohoúhelník vrcholy typu split nebo merge nemůže být monotónní.
Jestliže mnohoúhelník $P$ není monotónní, pak část jeho pravé nebo levé cesty mezi vrcholy $u$ a $d$ není klesající. Tedy existují na ní postupně vrcholy $p\ne d$ a $s\ne u$ takové, že
- cesta mezi $u$ a $p$ klesá a $p$ je minimální vrchol s touto vlastností,
- cesta mezi $s$ a $d$ klesá a $s$ je maximální vrchol s touto vlastností.
Jestliže bod $p$ má mnohoúhelník zdola, je vrcholem typu merge. Jestliže ho má shora, má ho shora i vrchol $s$, a proto je vrchol $s$ typu split.
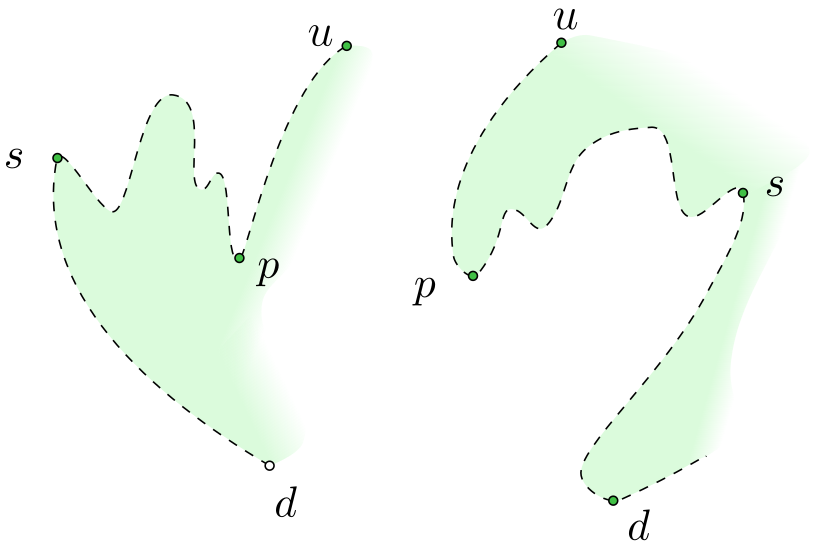
Obrázek 4.8
K důkazu věty 4.2.
\(\Box\)
Algoritmus pro dělení mnohoúhelníka na monotónní části
Cílem algoritmu bude přidávat v mnohoúhelníku $P$ spojnice vrcholů typu split a merge s dalšími vrcholy tak, abychom mnohoúhelník rozdělili na monotónní mnohoúhelníky, které již nebudou obsahovat žádné vrcholy těchto dvou typů. Spojnice z vrcholů typu split musí být tedy vedeny směrem nahoru, zatímco spojnice z vrcholů typu merge směrem dolů. Budeme to provádět metodou zametací přímky. Událostmi budou vrcholy mnohoúhelníka
seřazené podle popsaného lexikografického uspořádání od největšího (to je vrchol $u$) k nejmenšímu (vrchol $d$) do fronty $\mathcal Q$. Zametací přímka bude postupovat shora dolů a při přechodu událostí (= vrcholem) provedeme proceduru, která bude záviset na typu vrcholu a bude se týkat pouze "nejbližšího okolí" tohoto vrcholu nad zametací přímkou.
Toto „nejbližší okolí“ najdeme pomocí vyváženého binárního stromu $\mathcal T$, v jehož listech
budou strany mnohoúhelníka, které
- protínají zametací přímku a
- mají mnohoúhelník $P$ zprava.
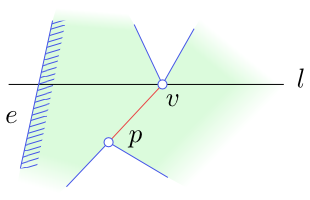
V popisu algoritmu hraje důležitou roli pojem pomocníka strany $e$ $(\operatorname{helper}(e))$. Vrchol $p$ mnohoúhelníka nazveme pro danou polohu zametací přímky $l$ pomocníkem strany $e$, která je
zametací přímkou protínána, jestliže
- $p$ leží nad zametací přímkou $l$,
- $p$ leží vpravo od úsečky $e$,
- horizontální úsečka spojující bod $p$ s úsečkou $e$ leží celá v mnohoúhelníku $P$,
- ze všech vrcholů splňujících předchozí podmínky má $p$ minimální $y$-ovou souřadnici
(je nejblíže nad zametací přímkou).
Ve stromě $\mathcal T$ budeme s každou stranou $e$ držet i jejího pomocníka.
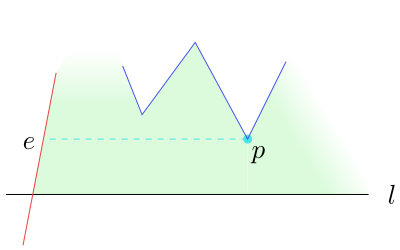
Obrázek 4.9
Bod $p$ je pomocník strany $e$.
Strategie algoritmu je následující. Vrcholy typu split odstraňujeme v okamžiku. kdy jimi prochází zametací přímka. V tomto případě spojíme tento vrchol s pomocníkem zleva nejbližší strany mnohoúhelníka. Tuto stranu najdeme pomocí binárního stromu $\mathcal T$.
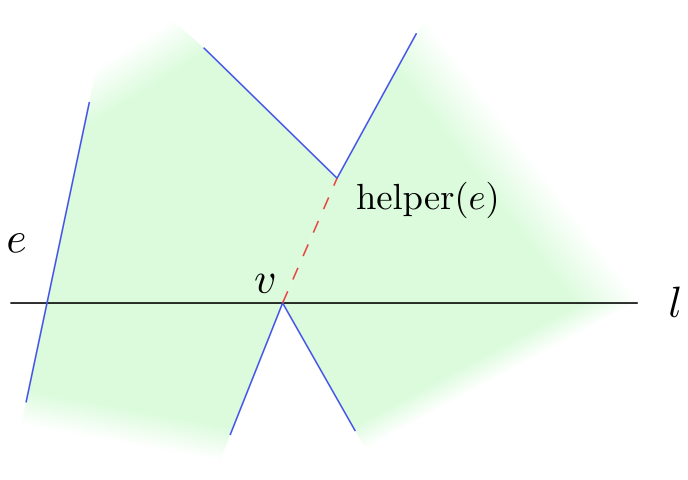
Obrázek 4.10
Odstranění split vrcholu $v$.
Odstranění vrcholů typu merge je složitější. Tyto vrcholy neodstraníme, když jimi zametací přímka prochází, neboť v tomto okamžiku neznáme „situaci“ pod zametací přímkou a nemůžeme vrchol spojovat s vrcholy pod ním. K odstranění merge vrcholů dochází zpětně. V každém z procházených vrcholů testujeme, zda pomocník jeho nejbližších stran je typu merge. Pokud ano, spojíme s ním daný vrchol.
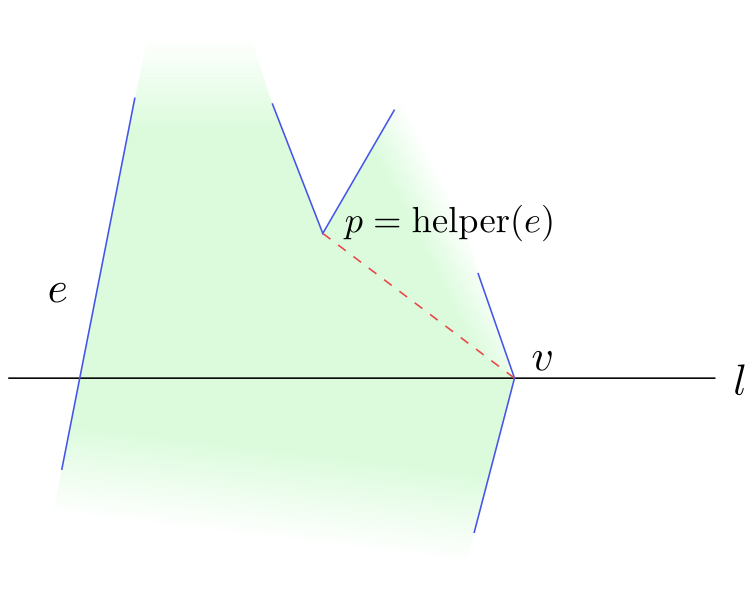
Obrázek 4.11
Odstranění merge vrcholu $p$.
Následující pseukód tvoří základní rámec algoritmu dělení na monotónní části.
Algorithm MakeMonotone($P$)
Input. A simple polygon $P$ stored in doubly-connected edge list $\mathcal D$.
Output. A partitioning of $P$ into monotone subpolygons, stored in $\mathcal D$.
- Construct a priority queue $\mathcal Q$ on the vertices of $P$, using their $y$-coordinates as priority. If two points have the same $y$-coordinate, the one with smaller $x$-coordinate has higher priority.
- Initialize an empty binary search tree $\mathcal T$.
- while $\mathcal Q$ is not empty
- do Remove the vertex $v_i$ with the highest priority $\mathcal Q$.
- Call the appropriate procedure to handle the vertex, depending on its type.
Procedury pro průchod různými typy vrcholů
Při průchodu zametací přímky událostmi provádíme následující akce:
- spojujeme vrchol s pomocníkem některé strany,
- do stromu $\mathcal T$ přidáváme strany mnohoúhelníka i s jejich pomocníky,
- měníme pomocníky některých stran ve stromu $\mathcal T$,
- ze stromu $\mathcal T$ odstraňujeme některé strany mnohoúhelníka.
Procedury pro konkrétní typy vrcholů jsou popsány a ilustrovány obrázky v následujícím textu.
Pro popis vrcholů mnohoúhelníka uspořádaných proti směru hodinových ručiček používáme značení $v_1$, $v_2$, $\dots$, $v_n$. Strana $e_i$ spojuje vrcholy $v_i$ a $v_{i+1}$, přičemž
bereme $v_{n+1}=v_1$.
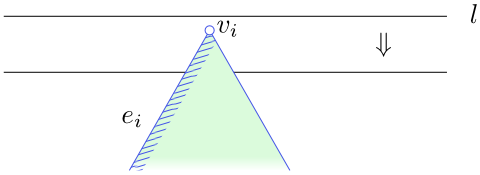
Obrázek 4.12
Průchod zametací přímky vrcholem typu start.
HandleStartVertex($v_i$)
- Insert $e_i$ in $\mathcal T$ and set $\operatorname{helper}(e_i)$ to $v_i$
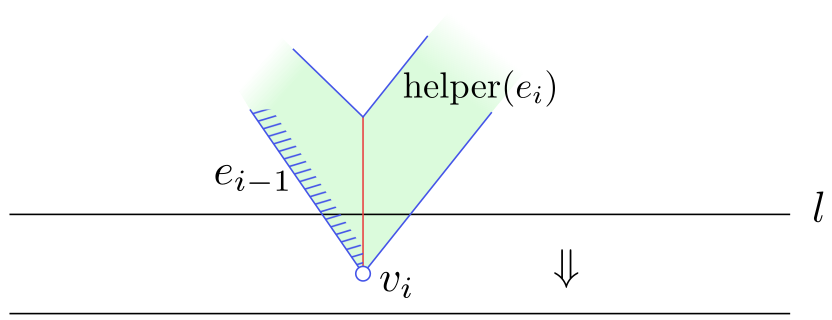
Obrázek 4.13
Průchod zametací přímky vrcholem typu end.
HandleEndVertex($v_i$)
- if $\operatorname{helper}(e_{i-1})$ is a merge vertex
- then Insert the diagonal connecting $v_i$ to $\operatorname{helper}(e_{i-1})$ in $\mathcal D$.
- Delete $e_{i-1}$ from $\mathcal T$.
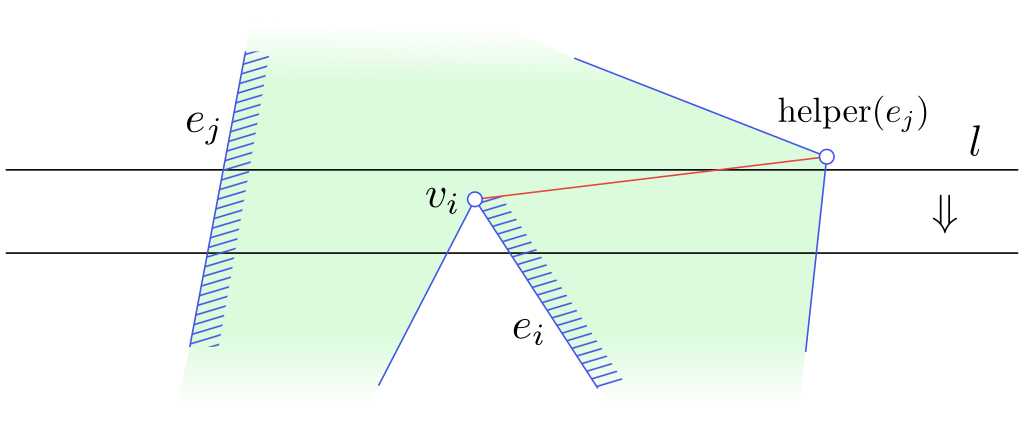
Obrázek 4.14
Průchod zametací přímky vrcholem typu split.
HandleSplitVertex($v_i$)
- Search in $\mathcal T$ to find the edge $e_j$ directly left of $v_i$.
- Insert the diagonal connecting $v_i$ to $\operatorname{helper}(e_j)$ in $\mathcal D$.
- $\operatorname{helper}(e_j)\leftarrow v_i$
- Insert $e_i$ in $\mathcal T$ and set $\operatorname{helper}(e_j)$ to $v_i$
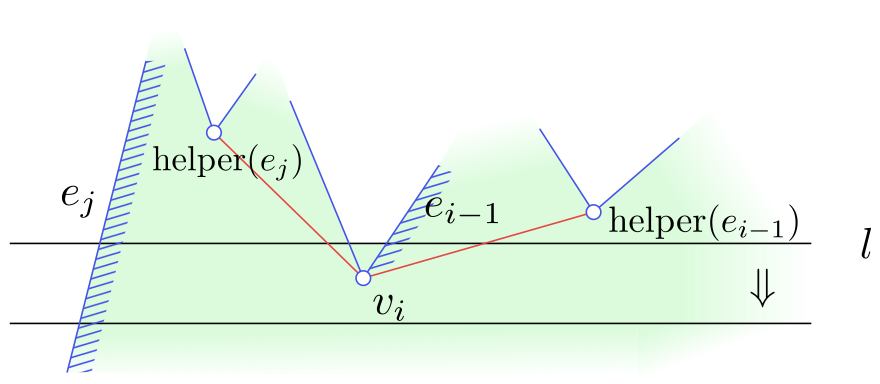
Obrázek 4.15
Průchod zametací přímky vrcholem typu merge.
HandleMergeVertex($v_i$)
- if $\operatorname{helper}(e_{i-1})$ is a merge vertex
- then Insert the diagonal connecting $v_i$ to $\operatorname{helper}(e_{i-1})$ in $\mathcal D$.
- Delete $e_{i-1}$ from $\mathcal T$
- Search in $\mathcal T$ to find the edge $e_j$ directly left of $v_i$.
- if $\operatorname{helper}(e_j)$ is a merge vertex
- then Insert the diagonal connecting $v_i$ to $\operatorname{helper}(e_j)$ in $\mathcal D$.
- $\operatorname{helper}(e_j)\leftarrow v_i$
Obrázek 4.16
Průchod zametací přímky vrcholem typu regular.
HandleRegularVertex($v_i$)
- if the interior of $\mathcal P$ lies to the right of $v_i$
- then if $\operatorname{helper}(e_{i-1})$ is a merge vertex
- then Insert the diagonal connecting $v_i$ to $\operatorname{helper}(e_{i-1})$ in $\mathcal D$.
- Delete $e_{i-1}$ from $\mathcal T$.
- Insert $e_i$ in $\mathcal T$ and set $\operatorname{helper}(e_i)$ to $v_i$.
- else Search in $\mathcal T$ to find the edge $e_j$ directly left of $v_i$.
- if $\operatorname{helper}(e_j)$ is a merge vertex
- then Insert the diagonal connecting $v_i$ to $\operatorname{helper}(e_j)$ in $\mathcal D$.
- $\operatorname{helper}(e_j)\leftarrow v_i$
Korektnost algoritmu a jeho časová náročnost
V důkazu korektnosti algoritmu bychom měli ukázat, že v průběhu algoritmu
- přidáváním spojnic vrcholů odstraníme všechny vrcholy typu split a merge,
- přidané spojnice vrcholů se navzájem neprotínají.
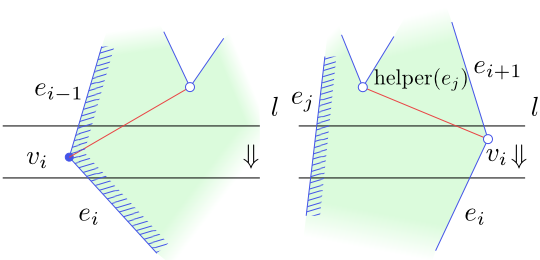
Se split vrcholy je to jednoduché. Odstraníme je, když jimi prochází zametací přímka. Jak je to s merge vrcholy? Každý merge vrchol $v$ je po průchodu zametací přímkou pomocníkem nějaké strany $e$. Odstraníme jej při průchodu vrcholem $p$, který leží pod $v$ a nahradí vrchol $v$ v roli pomocníka strany $e$.
Obrázek 4.17
Odstranění merge vrcholu $v$.
Důkaz, že se přidané hrany neprotínají, je potřeba provádět induktivně. Předpokládáme, že přidané spojnice nad zametací přímkou se neprotínají, a když dojdeme do vrcholu $v$, pak v závislosti od jeho typu musíme ukázat, že ani po provedení příslušné procedury, se přidané spojnice nebudou protínat. Je-li například $v$ split vrchol, pak v pásu mezi ním a pomocníkem $p$ nejbližší levé strany, žádná z dříve přidaných hran nemůže protínat nově přidanou spojnici
$vp$, protože jeden z jejích vrcholů by ležel v pásu
mezi zametací přímkou a vrcholem $p$, což je ve sporu s tím, že $p$ je
pomocníkem strany $e$, viz. obrázek.
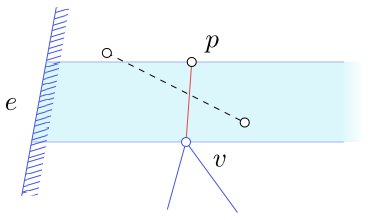
Obrázek 4.18
K předchozímu důkazu.
Věta 4.3
Časová náročnost algoritmu pro rozdělení jednoduchého $n$-úhelníka na monotonní mnohoúhelníky je $O(n\log n)$.
Důkaz
Seřazení vrcholů mnohoúhelníka do fronty $\mathcal Q$ trvá čas $O(n\log n)$.
Průchodem jednou událostí strávíme konstantní čas. Událostí je $n$. Tedy celková časová náročnost je $O(n\log n)+O(n)=O(n\log n)$.
\(\Box\)
Triangulace monotónních mnohoúhelníků
Uvažujme monotónní $n$-úhelník $P$.
Jeho levá a pravá cesta jsou klesající v daném lexikografickém uspořádání, proto můžeme
v čase $O(n)$ uspořádat vrcholy mnohoúhelníka od největšího k nejmenšímu do posloupnosti
$v_1$, $v_2$, $\dots$, $v_n$. Základní myšlenka našeho algoritmu pro triangulaci monotónního mnohoúhelníka je následující. Procházíme postupně vrcholy v daném uspořádání a vytváříme trojúhelníky spojnicemi s předchozími vrcholy, kdykoliv je to možné.
Místo fronty budeme v algoritmu používat zásobník (stack). Ten se vyznačuje tím, že vrcholy v něm jsou uspořádány v obráceném pořadí, než v jakém byly do zásobníku vkládány.
Na začátku algoritmu vložíme do zásobníku vrcholy $v_1$ a $v_2$, tedy zásobník bude
$\mathcal S=(v_2,v_1)$. Tyto dva body leží oba na levé nebo pravé cestě mnohoúhelníku $P$.
Jestliže následující vrchol $v_3$ leží na opačné cestě, spojíme jej s vrcholem $v_2$ a vznikne trojúhelník $v_1v_2v_3$. Přitom ze zásobníku nejdříve vyndáme $v_2$ a $v_1$ a pak vložíme
$v_2$ a $v_3$. Tedy zásobník bude $\mathcal S=(v_3,v_2)$.
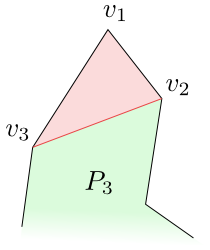
Obrázek 4.19
$v_3$ na opačné cestě než předchozí vrcholy.
Nechť nyní vrchol $v_3$ leží na stejné cestě jako vrcholy zásobníku. Jestliže úsečka $v_3v_1$ leží uvnitř $P$, body $v_3$ a $v_1$ spojíme a tím vznikne trojúhelník $v_1v_2v_3$. Ze zásobníku vyndáme $v_2$ a $v_3$ a vložíme do něj $v_1$ a $v_3$, tedy $\mathcal S=(v_3,v_1)$.
Jestliže úsečka $v_3v_1$ neleží v $P$, nemůžeme žádný trojúhelník vytvořit. V tomto případě
do zásobníku vložíme $v_3$. Tedy zásobník bude $\mathcal S=(v_3,v_2,v_1)$.
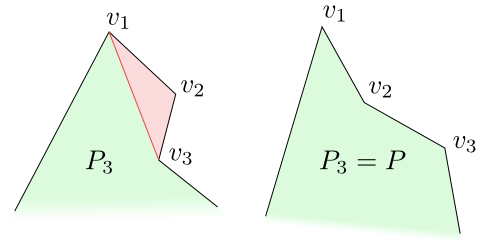
Obrázek 4.20
$v_3$ na stejné cestě jako předchozí vrcholy.
Nechť $P_3$ je mnohoúhelník $P$ bez trojúhelníka $v_1v_2v_3$, pokud tento trojúhelník leží v $P$, a nechť $P_3=P$ v opačném případě. Mnohoúhelník $P_3$ bude opět monotónní. V obou případech budou vrcholy v zásobníku ležet všechny na levé nebo pravé cestě mnohoúhelníka $P_3$. Tím jsme si popsali první krok algoritmu při průchodu vrcholem $v_3$.
Nyní přiblížíme krok algoritmu při průchodu vrcholem $v_j$ pro $4\leq j\leq n-1$. Nechť po průchodu předchozími vrcholy zbude z mnohoúhelníku $P$ po odřezání vzniklých trojúhelníků monotónní mnohoúhelník $P_{j-1}$. Nechť všechny vrcholy zásobníku
$$\mathcal S=(v_{i_1}, v_{i_2},\dots,v_{i_k}),\quad j-1=i_1\gt i_2\gt \dots\gt i_k\geq 1$$
leží na pravé nebo levé cestě mnohoúhelníka $P_{j-1}$.
Jestliže vrchol $v_j$ leží na opačné straně než vrcholy v zásobníku, vrchol $v_j$ se všemi vrcholy v zásobníku spojíme, zásobník vyprázdníme a vložíme do něj vrcholy $v_{j-1}$ a $v_j$. Tedy zásobník bude $\mathcal S=(v_j,v_{j-1})$. Vytvoříme také mnohoúhelník $P_j$ tak, že z mnohoúhelníku $P_{j-1}$ odřízneme nově vzniklé trojúhelníky.
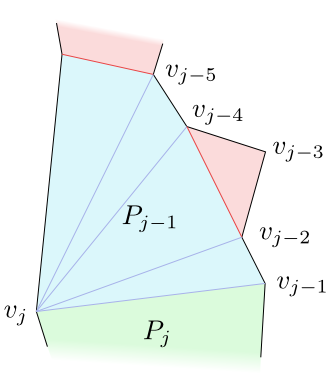
Obrázek 4.21
$v_j$ leží na na opačné cestě než vrcholy $v_{j-1}$, $v_{j-2}$, $v_{j-4}$, $v_{j-5}$ ze zásobníku.
Jestliže vrchol $v_j$ leží na stejné straně mnohoúhelníku $P_{j-1}$ jako vrcholy v zásobníku,
snažíme se vrchol $v_j$ spojovat postupně s vrcholy $v_{i_2}$, $v_{i_3}$, atd, pokud je to možné. To znamená, že pokud úsečka
$v_jv_{i_2}$ leží uvnitř $P_{j-1}$, vrcholy spojíme. Jestliže navíc také úsečka $v_jv_{i_3}$ leží uvnitř $P_{j-1}$, vrcholy rovněž spojíme. Postupujeme tak dlouho, dokud nenarazíme na vrchol zásobníku $v_{i_s}$ takový, že úsečka $v_jv_{i_s}$ uvnitř $P_{j-1}$ neleží. Ze zásobníku přitom vyndáme vrcholy $v_{i_1},v_{i_2},\dots,v_{i_{s-1}}$ a vložíme do něj vrcholy $v_{i_{s-1}}$ a $v_j$.
Mnohoúhelník $P_j$ vznikne opět z mnohoúhelníku $P_{j-1}$ odříznutím nově vzniklých trojúhelníků.
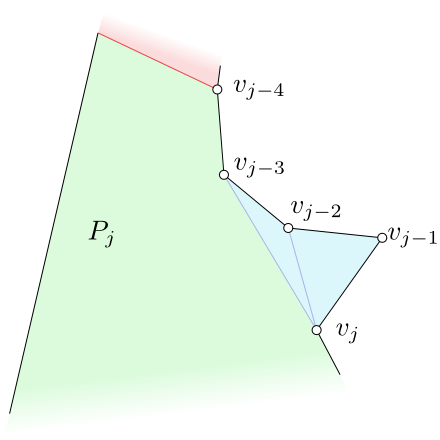
Obrázek 4.22
$v_j$ leží na stejné cestě jako vrcholy $v_{j-1}$, $v_{j-2}$, $v_{j-3}$, $v_{j-4}$ ze zásobníku.
Popsaný algoritmus je zachycen následujícím pseudokódem:
Algorithm TriangulateMonotonePolygon($\mathcal P$)
Input. A strictly $y$-monotone polygon $\mathcal P$ stored in a doubly-connected edge list $\mathcal D$.
Output. A triangulation of $\mathcal P$ stored in the doubly-connected edge list $\mathcal D$.
- Merge the vertices on the left chain and the vertices on the right chain of $\mathcal P$ into one sequence, sorted on decreasing $y$-coordinate. If two vertices have the same $y$-coordinate, then the leftmost one comes first. Let $v_1,\ldots, v_n$ denote the sorted sequence.
- Initialize an empty stack $\mathcal S$, and pust $v_1$ and $v_2$ onto it.
- for $j\leftarrow 3$ to $n-1$
- do if $v_j$ and the vertex on top of $\mathcal S$ are on different chains
- then Pop all vertices from $\mathcal S$.
Insert into $\mathcal D$ a diagonal from $v_j$ to each popped vertex, except the last one.
- Push $v_{j-1}$ and $v_j$ into $\mathcal S$.
- else Pop one vertex from $\mathcal S$.
Pop the other vertices from $\mathcal S$ as long as the diagonals from $v_j$ to them are inside $\mathcal P$. Insert these diagonals into $\mathcal D$. Push the last vertex that has been popped back onto $\mathcal S$.
- Push $v_j$ onto $\mathcal S$.
- Add diagonals from $v_n$ to all stack vertices except the first and the last one.
Triangulaci monotónního 11-úhelníku provedenou podle tohoto algoritmu zachycuje následující obrázek.
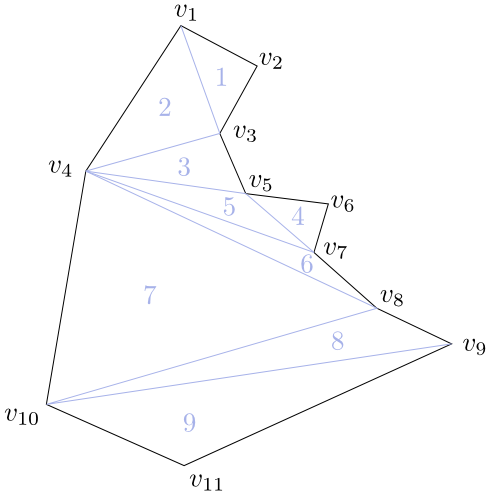
Obrázek 4.23
Trojúhelníky jsou očíslovány v pořadí, ve kterém byly algoritmem vytvořeny.
Věta 4.4
Časová náročnost algoritmu na triangulaci monotónního $n$-úhelníka je O(n).
Důkaz
Lexikografické uspořádání vrcholů monotónního mnohoúhelníka zabere čas
$O(n)$. V průběhu algoritmu je každý z $n$ vrcholů vložen a vyndán ze zásobníku nejvýše dvakrát. Při každém vložení a vyndání probíhají operace potřebující konstantní čas.
\(\Box\)