Lokalizace bodu

Úvod

Pro dané rovinné podrozdělení (mapu) chceme najít vyhledávací strukturu, která při zadání souřadnic bodu najde oblast, ve které bod leží. Idea algoritmu spočívá v tom, že si dané podrozdělení „zjemníme“ na tak zvanou lichoběžníkovou mapu a vyhledávací strukturu sestrojíme pro toto podrozdělení. Výhodou lichoběžníkové mapy je, že jednotlivé její oblasti jsou lichoběžníky a trojúhelníky (které lze považovat za deformované lichoběžníky) a ty lze relativně jednoduše popsat pouze pomocí 4 údajů.

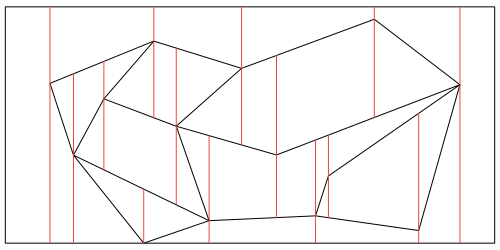
Obrázek 8.1
Vytvoření lichoběžníkové mapy.

Lichoběžníková mapa

Mějme rovinné podrozdělení (obvykle zadané pomocí dvojitě souvislého seznamu) ohraničené pravoúhelníkem $R$. Toto podrozdělení svými hranami určuje množinu úseček, které se neprotínají ve vnitřních bodech, ale mohou mít společné koncové body. Konstrukci lichoběžníkové mapy provedeme pro jakoukoliv množinu $n$ úseček

které leží v pravoúhelníku $R$. Pro další výklad budeme předpokládat, že žádné dva koncové body těchto úseček nemají stejnou $x$-ovou souřadnici. Tento omezující předpoklad odstraníme později. Levý koncový bod úsečky $s_i$ budeme značit $p_i$, pravý koncový bod $q_i$.

Lichoběžníkovou mapu $\mathcal T(S)$ sestrojíme tak, že každým koncovým bodem úsečky z množiny $S$ vedeme vertikální úsečku od nejbližší vyšší úsečky k nejbližší nižší úsečce, viz obrázek 8.2. Tím celý pravoúhelník $R$ rozdělíme na lichoběžníky a trojúhelníky.

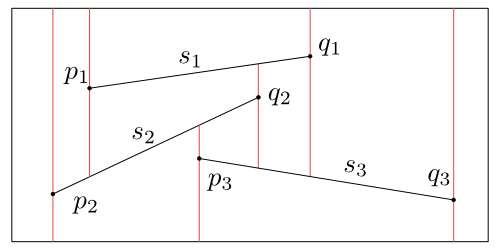
Obrázek 8.2
Lichoběžníková mapa pro tři úsečky.

Ukažme si, jak lichoběžníky a trojúhelníky z této mapy popsat pomocí úseček z množiny $S$ a jejich koncových bodů. Každý lichoběžník nebo trojúhelník $\Delta$ má dvě nevertikální strany, které jsou částí úseček z $S$ nebo částí horní nebo spodní strany pravoúhelníka $R$. Vrchní stranu tohoto lichoběžníku budeme označovat jako $\operatorname{top}(\Delta)$, spodní jako $\operatorname{bottom}(\Delta)$. Vertikální strany jsou určeny koncovými body $p_j$ nebo $q_j$ úseček z množiny $S$. V případě trojúhelníka přejde jedna z vertikálních stran do bodu. Proto je každý lichoběžník, resp. trojúhelník $\Delta$ kromě horní a spodní strany určen bodem $\operatorname{leftp}(\Delta)$, kterým vede levá vertikální strana, a bodem $\operatorname{rightp}(\Delta)$, kterým prochází pravá vertikální strana.

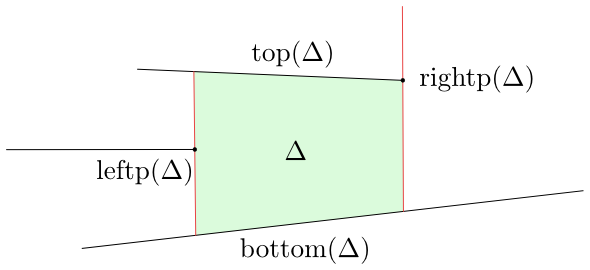
Obrázek 8.3
Popis lichoběžníku $\Delta$.

Podstatné je, že lichoběžníková mapa vytvořená pro $n$ úseček má řádově $n$ vrcholů a lichoběžníků.

Věta 8.1

Lichoběžníková mapa pro $n$ úseček má nejvýše $6n+4$ vrcholů a $3n+1$ lichoběžníků.

Důkaz

Celkový počet vrcholů lichoběžníkové mapy je dán vrcholy pravoúhelníka $R$ – ty jsou 4, koncovými body úseček – těch je nejvýše $2n$ a novými vrcholy, které byly vytvořeny nejvýše $2n$ vertikálami – těch je dvakrát tolik, kolik je vertikál, tedy nejvýše $4n$. Dohromady tedy nejvýše $6n+4$.

Počet lichoběžníků zjistíme tak, že pro každý bod určíme maximální počet lichoběžníků $\Delta$, pro které je tento bod levým bodem $\operatorname{leftp}(\Delta)$. Pro levý dolní vrchol pravoúhelníku $R$ existuje právě jeden takový lichoběžník. Pro pravý koncový $q_i$ úsečky $s_i$ existuje rovněž jeden lichoběžník, pro levý koncový bod $p_i$ existují 2 lichoběžníky.

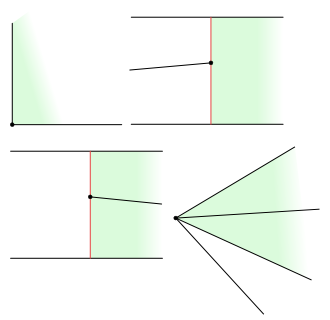
Obrázek 8.4
Počty lichoběžníků pro daný $\operatorname{leftp}$.

Vzhledem k tomu, že některé z koncových bodů úseček splývají (v takovém případě některé lichoběžníky započteme vícekrát), bude počet lichoběžníků nejvýše

$$1+n+2n=3n+1.$$

\(\Box\)

Vyhledávací struktura

Vyhledávací struktura pro lichoběžníkovou mapu $\mathcal T(S)$ slouží k určení lichoběžníku, v němž leží zadaný bod $r$, který neleží na žádné úsečce a jehož $x$-ová souřadnice je různá od $x$-ových souřadnic bodů $p_i$ a $q_i$. Je to orientovaný graf $\mathcal D(S)$ s těmito vlastnostmi:

• V listech tohoto grafu jsou všechny lichoběžníky z $\mathcal T(S)$.
• Z každého vnitřního uzlu vedou dvě hrany.
• Vnitřní uzly jsou dvojího typu.
• S prvým typem uzlů jsou svázány body $p_i$ a $q_i$. Z takového uzlu (označme jej na chvíli jako $p$) postupujeme vlevo, je-li pro $x$-ové souřadnice $r_x\lt p_x$, a vpravo, je-li $r_x\gt p_x$.
• S druhým typem uzlů jsou spojeny úsečky $s_i$. Z takového uzlu postoupíme vlevo, jestliže bod $r$ leží pod úsečkou $s_i$, a vpravo, je-li $r$ nad $s_i$.

Zatímco pro zadanou množinu $S$ je lichoběžníková mapa určena jednoznačně, tak vyhledávací struktura s výše uvedenými vlastnostmi určena jednoznačně není. Následující obrázky zachycují jednoduché příklady lichoběžníkových map a příslušných vyhledávacích struktur.

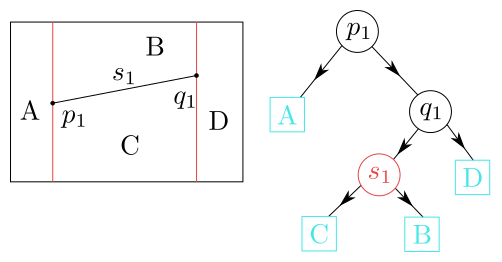
Obrázek 8.5
Lichoběžníková mapa a vyhledávací struktura pro 1 úsečku.

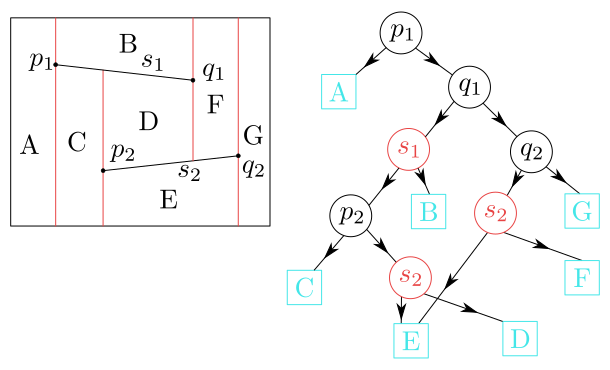
Obrázek 8.6
Lichoběžníková mapa a vyhledávací struktura pro 2 úsečky.

Délka cesty od kořene k listu odpovídá času pro vyhledání nějakého bodu v lichoběžníku, který danému listu odpovídá. Na obrázcích si všimněte podstatně odlišné délky cest k různým listům.

Náhodnostní přírůstkový algoritmus

Lichoběžníková mapa pro prázdnou množinu úseček je tvořena pouze pravoúhelníkem $R$, příslušná vyhledávací struktura obsahuje pouze jediný uzel a to list odpovídající pravoúhelníku $R$. Označíme-li

tak podstata algoritmu spočívá v tom, jak z lichoběžníkové mapy a vyhledávací struktury pro $i-1$ úseček z $S_{i-1}$ vytvořit lichoběžníkovou mapu $\mathcal T(S_i)$ a vyhledávací strukturu $\mathcal D(S_i)$ pro množinu úseček $S_i$. Vzhledem k tomu, že vyhledávací struktura závisí na pořadí úseček, bereme toto pořadí náhodně. Rámcově je algoritmus zachycen v následujícím pseudokódu:

Sledování úsečky

Nyní si ukážeme, jak pracuje algoritmus stručně popsaný 4. řádkem předchozího pseudokódu. Mějme lichoběžníkovou mapu $\mathcal T$ a vyhledávací strukturu $\mathcal D$ pro množinu $S_{i-1}$. Do pravoúhelníka $R$ přidáme úsečku $s=s_i$ s levým krajním bodem $p$ a pravým krajním bodem $q$ a chceme najít lichoběžníky $\Delta_0$, $\Delta_1$, $\dots,\ \Delta_k$, které úsečka $s$ protíná postupně zleva doprava.

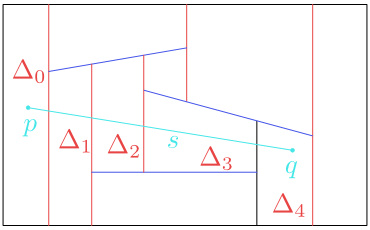
Obrázek 8.7
Úsečka $s$ prochází postupně lichoběžníky $\Delta_0, \Delta_1,\Delta_2,\Delta_3,\Delta_4$.

K popisu tohoto algoritmu budeme potřebovat pojem sousedních lichoběžníků a levého a pravého souseda. O dvou lichoběžnících prohlásíme, že jsou sousední, mají-li společnou část vertikální strany, která nedegeneruje do bodu.

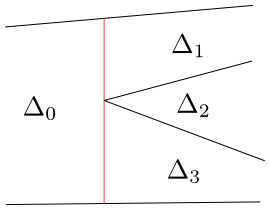
Obrázek 8.8
Dvojice lichoběžníků $\Delta_0$ a $\Delta_1$, $\Delta_0$ a $\Delta_3$ jsou sousední, zatímco dvojice $\Delta_0$ a $\Delta_2$ nebo $\Delta_1$ a $\Delta_2$ sousední nejsou.

Mají-li dva sousední lichoběžníky společnou spodní stranu, řekneme, že jeden je (levým nebo pravým) dolním sousedem druhého. Mají-li společnou horní stranu, řekneme, že jeden je (levým nebo pravým) horním sousedem druhého.

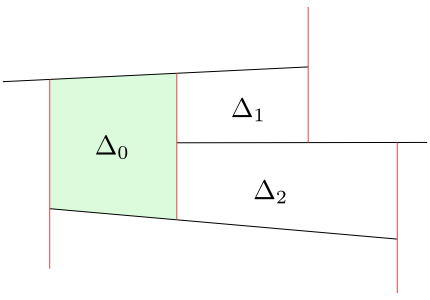
Obrázek 8.9
Lichoběžník $\Delta_1$ je pravým horním sousedem lichoběžníku $\Delta_0$. Lichoběžník $\Delta_0$ je levým dolním sousedem lichoběžníku $\Delta_2$.

Algoritmus najde prvně lichoběžník $\Delta_0$, ve kterém leží levý krajní bod $p$ úsečky $s$. Jestliže bod $p$ není levým koncovým bodem žádné úsečky z $S_{i-1}$, stačí k nalezení $\Delta_0$ použít vyhledávací strukturu $\mathcal D$. Jestliže je $p$ je levým koncovým bodem jedné nebo více úseček z $S_{i-1}$, leží vpravo od něj více lichoběžníků a my si z nich musíme vybrat ten, kterým prochází úsečka $s$. To provedeme porovnáním směrnic těchto úseček se směrnicí úsečky $s$. Směrnice této úsečky s krajními body $p$ a $q$ je rovna podílu rozdílů $y$-ových a $x$-ových souřadnic

Hledaný lichoběžník $\Delta_0$ se vyznačuje tím, že směrnice jeho horní strany je větší než směrnice úsečky $s$ a ta je větší než směrnice jeho spodní strany.

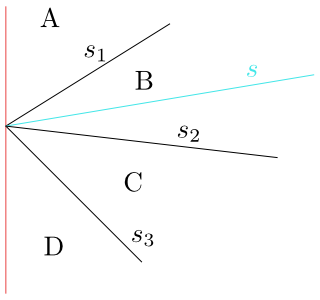
Obrázek 8.10
Směrnice úsečky $s_1$ $>$ směrnice $s$ $>$ směrnice $s_2$. Hledaným lichoběžníkem $\Delta_0$ je lichoběžník $B$.

Jestliže bod $q$ leží vlevo od $\operatorname{rightp}(\Delta_0)$, leží v $\Delta_0$ celá úsečka $s$.

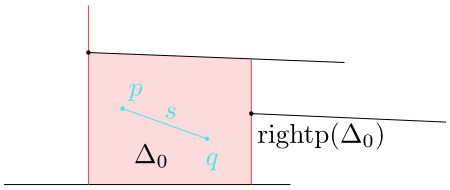
Obrázek 8.11
Celá úsečka $s$ leží v $\Delta_0$.

Jestliže bod $q$ leží vpravo od $\operatorname{rightp}(\Delta_0)$, protíná úsečka $s$ ještě další lichoběžník $\Delta_1$. Tímto lichoběžníkem je dolní pravý soused lichoběžníku $\Delta_0$, jestliže $\operatorname{rightp}(\Delta_0)$ leží nad $s$, a pravý horní soused, pokud $\operatorname{rightp}(\Delta_0)$ leží pod $s$, viz následující obrázek.

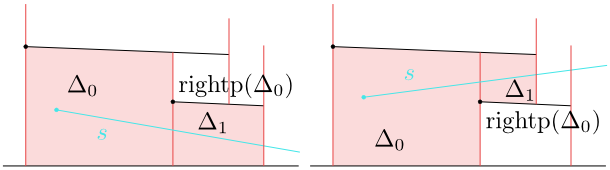
Obrázek 8.12
Určení $\Delta_1$ podle vzájemné polohy úsečky $s$ a bodu $\operatorname{rightp}(\Delta_0)$.

Stejným způsobem postupujeme dále, jak zachycuje následující pseudokód:

Nahrazení protínaných lichoběžníků novými a modifikace vyhledávací struktury

V této části si ukážeme základní myšlenku algoritmu, který realizuje 5. a 6. řádek algoritmu TrapezoidalMap, tj. jak lichoběžníky $\Delta_0$, $\Delta_1$, $\dots,\ \Delta_k$ protínané úsečkou $s=s_i$ nahradíme v lichoběžníkové mapě $\mathcal T$ novými lichoběžníky a jak změníme vyhledávací strukturu $\mathcal D$

Předpokládejme prvně, že úsečka $s$ leží celá uvnitř jediného lichoběžníku $\Delta_0$.

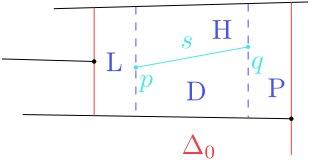
Obrázek 8.13
Úsečka $s$ leží celá v lichoběžníku $\Delta_0$.

V tomto případě je lichoběžník $\Delta_0$ v $\mathcal T$ nahrazen lichoběžníky $L$, $H$, $D$ a $P$. Každý z těchto lichoběžníků je určen svou horní a dolní stranou a pravým a levým bodem. Například pro lichoběžník $H$ je

Modifikaci vyhledávací struktury provedeme tak, jak je ukázáno na následujícím obrázku.

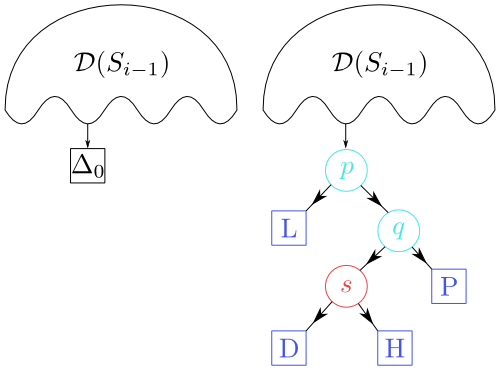
Obrázek 8.14
Přechod od $\mathcal D(S_{i-1})$ k $\mathcal D(S_i)$.

Nechť nyní úsečka $s$ protíná více mnohoúhelníků. Pro názornost uvažujme situaci znázorněnou na prvním z následujících dvou obrázků

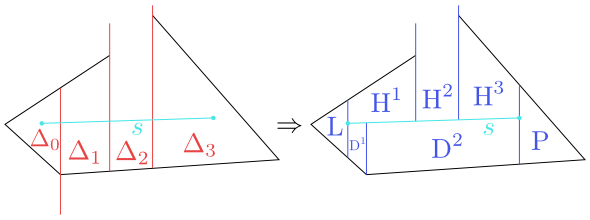
Obrázek 8.15
Přechod od $\mathcal T(S_{i-1})$ k $\mathcal T(S_i)$.

Nahrazení lichoběžníků $\Delta_0$, $\Delta_1$, $\Delta_2$, $\Delta_3$ novými lichoběžníky provedeme takto. $L$ je lichoběžník ležící vlevo od bodu $p$, má stejné $\operatorname{top}$, $\operatorname{bottom}$ a $\operatorname{leftp}$ jako $\Delta_0$. Protože $\operatorname{rightp}(\Delta_0)$ leží pod $s$, je dalším lichoběžníkem $D^1$ s

Pravý bod lichoběžníku $\Delta_1$ leží nad $s$, proto další lichoběžník leží nad $s$. Označme ho jako $H^1$. Je určen těmito údaji

Pravý bod lichoběžníku $\Delta_2$ leží opět nad $s$, proto také další lichoběžník $H^2$ bude nad $s$ a přitom

Protože v dalším lichoběžníku $\Delta_3$ leží pravý koncový bod $q$ úsečky $s$, doplníme seznam nových lichoběžníků o lichoběžník $D^2$ ležící pod $s$ s pravým bodem $q$, o lichoběžník $H^3$ ležící nad $s$ s pravým bodem $q$ a o lichoběžník $P$ ležící vpravo od bodu $q$.

Modifikaci vyhledávací struktury znázorňuje následující obrázek.

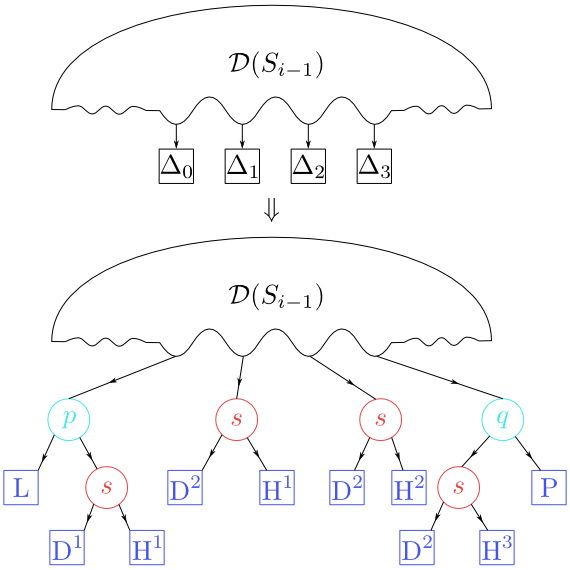
Obrázek 8.16
Přechod od $\mathcal D(S_{i-1})$ k $\mathcal D(S_i)$.

Pseudokódy pro aktualizaci lichoběžníkové mapy $\mathcal T$ a vyhledávací struktury $\mathcal D$ nebudeme explicitně uvádět. Čtenář si je může na základě předchozích úvah napsat již sám nebo se na ně podívat do bakalářské práce Ondřeje Folvarčného http://is.muni.cz/auth/th/211164/prif_b/BP.pdf?lang=cs na stranách 20 a 21.

Odstranění zjednodušujících předpokladů

Zjednodušení spočívalo v tom, že různé koncové body úseček a vyhledávaný bod $r$ měly různé $x$-ové souřadnice. Tento předpoklad odstraníme zavedením transformace souřadnic (shear transformation)

pro malé $\varepsilon>0$.

Nyní bychom tedy mohli v předchozích úvahách nahradit uspořádání podle $x$-ové souřadnice uspořádáním podle $x$-ové souřadnice $\varphi$. Ve skutečnosti však žádné $\varepsilon$ pro určení transformace $\varphi$ není potřeba počítat.

Z předchozích úvah můžeme učinit tento praktický závěr: Kdykoliv v předchozích úvahách zjišťujeme, zda je bod vlevo či vpravo od jiného bodu, použijeme lexikografické uspořádání. Kdykoliv zjišťujeme zda nějaký bod leží nad nebo pod nějakou úsečkou, použijeme uspořádání podle $y$-ové souřadnice.

Odhady složitosti

Vzhledem k tomu, že náš algoritmus je náhodnostní, provedeme odhad očekávané náročnosti jednak na čas konstrukce vyhledávací struktury, jednak na paměť potřebnou pro uložení vyhledávací struktury a konečně na čas vyhledávání bodu pomocí této vyhledávací struktury. Začneme posledním údajem.

Věta 8.4

Očekávaný čas vyhledávání ve struktuře $\mathcal D$ vytvořené náhodným uspořádáním úseček je $O(\log n)$.

Důkaz

Vyhledávací strukturu $\mathcal D$ vytvoříme v $n$ krocích. Nechť $X_i$ je počet uzlů na cestě při vyhledávání bodu $r$, které byly přidány v $i$-tém kroku. Z toho, jak jsme modifikovali vyhledávací strukturu (viz obrázky 8.14 a 8.16) je vidět, že

$$0\le X_i\le 3.$$

Považujme $X_i$ za náhodnou veličinu. Potom očekávaný čas vyhledávání je

$$E\left(\sum_{i=1}^n X_i\right)=\sum_{i=1}^n E(X_i)\le 3\cdot\operatorname{pravděpodobnost}(X_i\ne 0).$$

Skutečnost, že $X_i\ne 0$ znamená, že vyhledávaný bod $r$ leží v $\mathcal T(S_i)$ v nějakém lichoběžníku $\Delta$, který vznikl právě v $i$-tém kroku při přidání úsečky $s_i$. To znamená, že nastane aspoň jedna z následujících možností:

$$\operatorname{top}(\Delta)=s_i,\ \operatorname{bottom}(\Delta)=s_i,\\ \operatorname{leftp}(\Delta)=p_i\ \text{nebo}\ q_i,\ \operatorname{rightp}(\Delta)=p_i\ \text{nebo}\ q_i.$$

Pravděpodobnost, že aspoň jedna z těchto možností nastane je nejvýše $4/i$. Očekávaný čas vyhledávání je tedy shora odhadnut součtem

$$3\left(\sum_{i=1}^n \frac{4}{i}\right)=12\left(1+\sum_{i=2}^n\frac{1}{i}\right)\le 12\left(1+\int_1^n \frac{dx}{x}\right)=12(1+\log n)\\=O(\log n).$$

Prostřední odhad pomocí integrálu plyne z toho, že součet obsahů obdélníků o stranách $1$ a $1/i$ pro $i=2,3,\dots,n$ je menší než obsah oblasti mezi osou $x$ a grafem funkce $1/x$ mezi čísly $1$ a $n$ na ose $x$, viz obrázek.

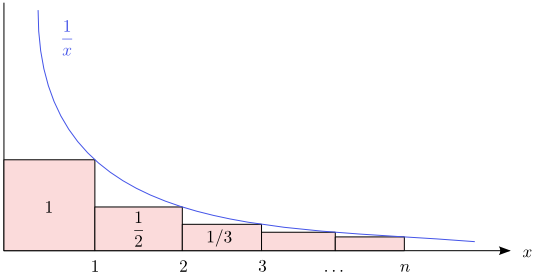
Obrázek 8.17
Porovnání součtu $\frac{1}{2}+\frac{1}{3}+\dots +\frac{1}{n}$ s integrálem $\int_{1}^{n}\frac{dx}{x}$.

\(\Box\)