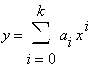
Mnohem vhodnější bude změřené pozice bodů interpolovat, tedy uvažovat křivku, která bude blízká těmto bodům. Jedná se nám o to, aby odchylky (respektive vzdálenosti) změřených bodů od aproximační křivky byly minimální. Pro funkce je vhodnější brát druhou mocninu vzdáleností empiricky zjištěných bodů od teoreticky spočítaných na křivce (y-ové souřadnice pro dané x-ové souřadnice), než složitě počítat s Eukleidovskými vzdálenostmi. Proces aproximace vysvětlíme na příklady polynomiální křivky o rovnici:
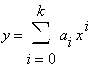
Jedná se nám o určení parametrů této křivky. Tedy máme polynom stupně k a potřebujeme n≥k+1 bodů na obryse vajíčka. Opět uvažujme jen jeho polovinu určenou osou vajíčka (celý model vajíčka vznikne rotací interpolační křivky kolem této osy). Pro jednoduchost umístíme obrys vajíčka do kartézského systému souřadnic 0xy, kde osa vajíčka bude totožná s osou x a průměr vajíčka (spojuje nejvzdálenější body vajíčka od jeho osy) ztotožníme s osou y. Pro jednoznačnost tohoto přiřazení ještě dodejme, že špička vajíčka bude protínat osu x v její kladné části. Pak lze jednotně zkoumat různá vajíčka a obdržíme vždy podobné rovnice. Budeme dále uvažovat jen polovinu obrysu vajíčka, například ležící nad osou x. Tedy chceme-li obrys vajíčka interpolovat polynomiální křivkou stupně k=5, pak potřebujeme určit polohu n≥6 bodů o souřadnicích [x,y]. Nyní spočítáme součet druhých mocnic těchto odchylek podle vzorce:
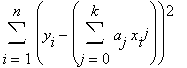
Hledáme parametry tak, aby uvedený součet byl minimální, tedy určíme parciální derivace podle x,y a ty položíme rovny nule (bod ve kterém může nastat extrém). Dostáváme soustavu rovnic, jejichž řešením jsou hledané parametry:

Tak například pro vajíčko poštolky obecné odečteme souřadnice 10 bodů:
![]()
Tyto souřadnice dosadíme do spočítaných vzorců a dostáváme parametry naší aproximační polynomiální křivky (pátého stupně):
![]()
![]()
![]()
![]()
![]()
![]()
Aproximace je tedy vhodnější, neboť nám ubylo parametrů pro určení křivky a se vzrůstajícím počtem měření se zlepšuje i přesnost (součet čtverců, podle nějž byla tato metoda pojmenována, se však zvyšuje). V případě n=k+1 dochází přímo k interpolaci, jak byla již dříve popsána. Pro naše účely však ani tento přístup není příliš účelný. Proto ve zbývajícím prostoru popišíme ještě jeden, poslední, postup, který se zdá být nejvhodnějším.