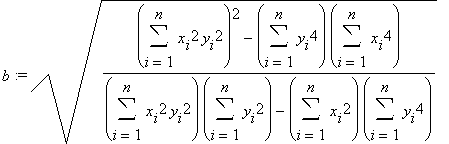Mějme dáno n bodů roviny [xi,yi], kde i=1,...,n a předpokládejme, že leží na křivce blízké elipse se středem v počátku kartézské soustavy souřadnic o rovnici:

Považujme a,b za reálná kladná čísla (délky příslušných poloos). Proveďme substituci za parametry naší rovnice:

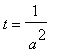
![]()
Pak i s,t jsou reálná čísla. Nyní požadujeme, aby součet vzdáleností daných bodů od hledané elipsy byl co nejmenší. Pak výsledná elipsa bude nejlépe odpovídat průběhu zadaných bodů. Ulehčíme si však výpočty (takto popsaný postup přesahuje rámec středoškolské matematiky). Dosadíme-li do levé strany hledané rovnice elipsy libovolný zadaný bod, pak v případě, že skutečně leží na této elipse, dostaneme výsledek 0. Pokud leží uvnitř elipsy, pak vyjde kladné číslo. Pokud vně, tak záporné. Jestliže umocníme toto číslo na druhou, pak jistě dostaneme nezáporné číslo (tím menší, čím blíže je bod elipse). Součet všech těchto čísel bude tedy také nezáporné číslo (0 pokud všechny body leží na hledané elipse). Za předpokladu, že body leží s jistou pravděpodobností na elipse, tedy můžeme pokračovat dál. Pokud bychom neumocnili, mohl by vyjít celkový součet 0 přesto, že body na elipse neleží a odchylky jsou velmi významné. Pro celkový součet dostáváme vzorec:

Jak jsme uvedli požadujeme, aby uvedený součet byl minimální. Hledejme tedy stacionární body dané funkce 2 proměnných (derivujeme součet nejdříve po řadě podle s a t), které tedy vyhovují zároveň rovnicím:

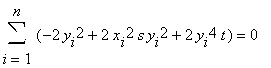
Tato lineární soustava 2 rovnic o 2 neznámých má jediné řešení pro n≥2 (právě hledané minimum):

Nyní se vraťme zpět k substituci a obdržíme vzorce pro výpočet délek poloos hledané elipsy: