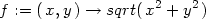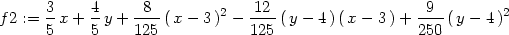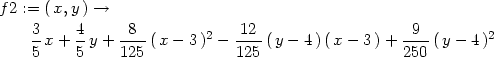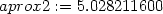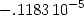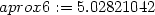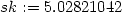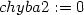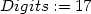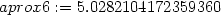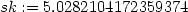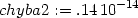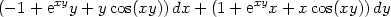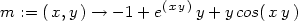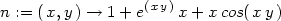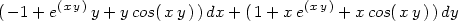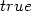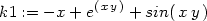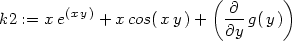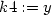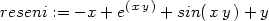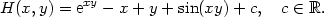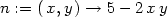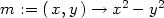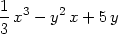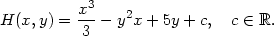Kapitola 13
Aproximace funkce v
Maplu
V této kapitole se opět nabízí bohaté
využití jak grafických, tak i výpočetních možností počítačového
systému. Postupně si všimneme zejména grafických možností při
ilustraci pojmů diferencovatelná funkce a tečná rovina, výpočetních
možností při určování diferenciálů a při přibližných výpočtech
pomocí diferenciálu. Na závěr použijeme počítače při hledání
kmenové funkce.
13.1 Diferencovatelná
funkce
Pomocí počítačové grafiky nyní ilustrujme pojem
diferencovatelná funkce a vztahy mezi diferencovatelností,
spojitostí a existencí parciálních derivací.
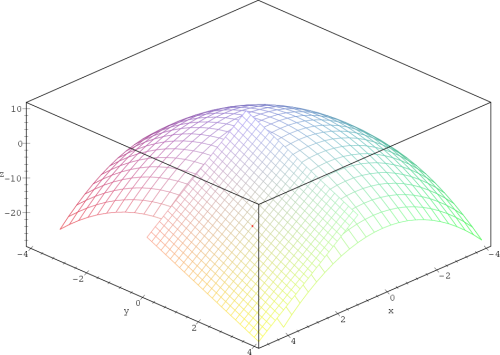
Příklad 13.1. Funkce
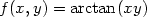
je diferencovatelná v bodě
[0,0]
(obr.
13.1
), protože má v tomto bodě spojité
parciální derivace (Věta
4.3
).
Ověřme spojitost parciálních derivací:
> f:=(x,y) -> arctan(x*y);
> plot3d(f(x,y),x=-3..3,y=-3..3,axes=framed,
> grid=[20,20],orientation=[-50,40],labels=[x,y,z],
> style=patch);
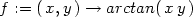
> dx:=D[1](f);
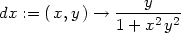
> dx(0,0);
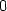
> dy:=D[2](f);
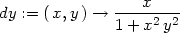
> dy(0,0);
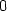
Limity lim(x,y) (0,0)
(0,0)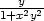 a lim(x,y)
a lim(x,y)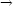 (0,0)
(0,0)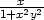 určíme dosazením
souřadnic limitního bodu:
určíme dosazením
souřadnic limitního bodu:
> limit(dx(x,y),{x=0,y=0});
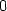
> limit(dy(x,y),{x=0,y=0});
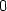
tedy limita parciálních derivací v bodě
[0,0] je
rovna jejich funkční hodnotě v tomto bodě a parciální derivace
jsou v bodě [0,0]
spojité.
Ze samotné existence parciálních derivací funkce
v bodě [x0,y0] však
diferencovatelnost neplyne.
Příklad 13.2. Funkce
![{ -x2y-, [x,y] ⁄= [0,0], f (x,y) = x2+y2 0, [x,y] = [0,0]](diferencialni-pocet1316x.png)
není v bodě
[0,0]
diferencovatelná (PC-graf obr.
11.2
), i když má v bodě
[0,0] obě
parciální derivace (rovny nule).
Tuto skutečnost ukážeme pomocí definice. Zjistěme nejprve, zda
existují parciální derivace funkce
f v bodě
[0,0]:
> f:=(x,y)->if x=0 and y=0 then 0
> else (x^2*y)/(x^2+y^2) fi:
> A:=subs(x=0,y=0,diff(f(x,y),x));
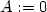
> B:=subs(x=0,y=0,diff(f(x,y),y));
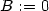
To znamená, že obě vyšetřované parciální derivace
existují a jsou rovny nule. Má-li být funkce f diferencovatelná
v bodě [0,0],
musí podle definice platit
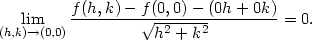
Vypočtěme limitu na levé straně této rovnosti:
> l:=(f(h,k)-f(0,0)-(A*h+B*k))/(sqrt(h^2+k^2));
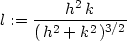
Transformací do polárních souřadnic
dostáváme:
> Limit(subs(h=r*cos(phi), k=r*sin(phi), l), r=0,
> right)=simplify(limit(subs(h=r*cos(phi),
> k=r*sin(phi), l), r=0, right));
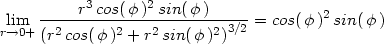
Výsledek závisí na  , tedy daná limita neexistuje, a proto
funkce f není
v bodě [0,0]
diferencovatelná.
, tedy daná limita neexistuje, a proto
funkce f není
v bodě [0,0]
diferencovatelná.
Je–li funkce f(x,y)
v bodě [x0,y0] spojitá,
nemusí být v tomto bodě diferencovatelná (ze spojitosti
v bodě [x0,y0] neplyne
diferencovatelnost v tomto bodě).
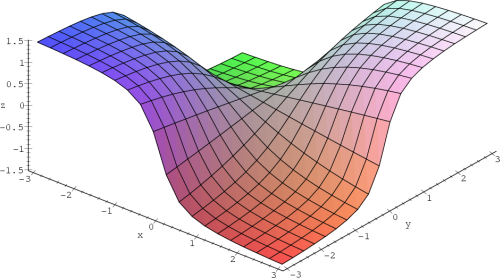
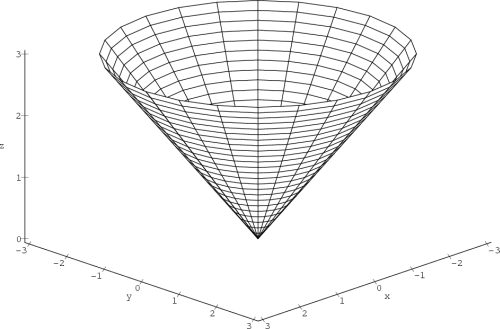
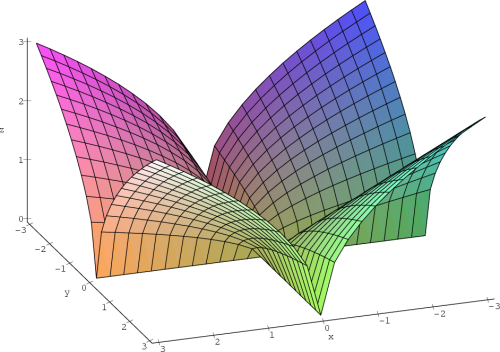
Příklad 13.3. Funkce
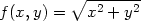
je v bodě
[0,0]
spojitá, ale není v tomto bodě diferencovatelná, protože
v tomto bodě neexistují parciální derivace (obr.
13.2).
> f:=(x,y)->sqrt(x^2+y^2):
> plot3d([r*cos(u), r*sin(u), r], r=0..3, u=0..2*Pi,
> axes = framed,orientation=[45,60],shading=none,
> tickmarks=[7,7,4],labels=[x,y,’z’]);
Ověřme spojitost: platí
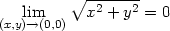
a
f(0,0) = 0,
tj. funkce
f je v bodě
[0,0]
spojitá.
Ukažme, že neexistují parciální derivace
v bodě [0,0].
Funkce f je symetrická vzhledem
k proměnným x a
y, proto stačí vyšetřit jen
parciální derivaci podle x.
Podle definice platí:
> Limit((f(x,0)-f(0,0))/(x-0), x=0, left)=
> limit((f(x,0)-f(0,0))/(x-0), x=0, left);
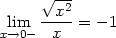
> Limit((f(x,0)-f(0,0))/(x-0), x=0, right)=
> limit((f(x,0)-f(0,0))/(x-0), x=0, right);
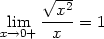
Jednostranné limity jsou různé, tedy parciální
derivace podle x a y v bodě [0,0]
neexistují a funkce f není
v tomto bodě diferencovatelná.
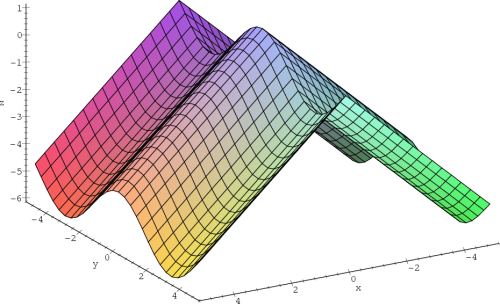
Příklad 13.4. Funkce
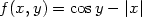
není diferencovatelná v bodech
[0,y]
(obr.
13.3
).
> f:=(x,y)->cos(y)-abs(x);
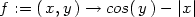
> plot3d(f(x,y),x=-5..5,y=-5..5,axes=framed,
> grid=[31,29],orientation=[60,60],style=patch,
> labels=[x,y,’z’]);
Ukažme, že v bodech [0,y]
neexistují parciální derivace podle x:
> Limit((f(x,y0)-f(0,y0))/x, x=0, left) =
> limit((f(x,y0)-f(0,y0))/x, x=0, left);
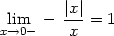
> Limit((f(x,y0)-f(0,y0))/x, x=0, right) =
> limit((f(x,y0)-f(0,y0))/x, x=0, right);
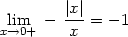
Limita zleva se nerovná limitě zprava a tedy
parciální derivace podle x
v bodech [0,y]
neexistují.
Příklad 13.5. Funkce
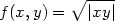
je diferencovatelná v
 2
2
s výjimkou bodů osového kříže, tj. bodů
[x,y],
kde
x = 0 nebo
y = 0
(obr.
13.4
).
> f:=(x,y)->sqrt(abs(x*y));
> plot3d(f(x,y), x=-3..3, y=-3..3, axes=framed,
> style=patch, orientation=[70,55], tickmarks=[7,7,4],
> labels=[x,y,’z’]);
Najděme body, ve kterých existují a jsou spojité
obě parciální derivace fx
a fy. Podle Věty 4.3
je v takových bodech funkce
diferencovatelná. Přímým derivováním dostaneme
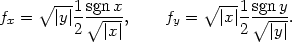
Tyto derivace jsou spojité na
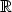 2
2
kromě obou os
x = 0 a
y
= 0, které je třeba vyšetřit
zvlášť.
Nejprve vyšetříme parciální derivace podle
x v bodech ležících na ose
y kromě počátku [0,0].
Uvažujme proto body [0,y0],
y0≠0
libovolné. Podle definice derivace je:
> Limit((f(x,y[0])-f(0,y[0]))/x, x=0, left)=
> limit((f(x,y[0])-f(0,y[0]))/x, x=0, left);
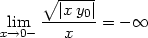
> Limit((f(x,y[0])-f(0,y[0]))/x, x=0, right)=
> limit((f(x,y[0])-f(0,y[0]))/x, x=0, right);
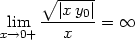
Jednostranné limity se nerovnají, ve vyšetřovaných
bodech neexistuje parciální derivace podle x. Ze symetrie funkce f vzhledem k x a y
plyne stejný výsledek pro parciální derivaci fy(x0,0),
x0≠0. To
znamená, že na osách x,
y kromě bodu [0,0] není
funkce f(x,y)
diferencovatelná.
Zbývá vyšetřit diferencovatelnost v bodě
[0,0].
Opět nejprve vypočtěme parciální derivace:
> A:=limit((f(x,0)-f(0,0))/x, x=0);
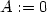
> B:=limit((f(0,y)-f(0,0))/y, y=0);
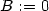
tj. v bodě [0,0] obě
parciální derivace existují a jsou rovny nule. Podle definice
diferencovatelnosti musí platit
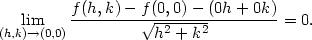
Vyšetřeme limitu na levé straně rovnosti. Přechodem k polárním
souřadnicím dostáváme:
> l:=(f(h,k)-f(0,0)-(A*h+B*k))/(sqrt(h^2+k^2));
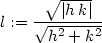
> Limit(subs(h=r*cos(phi), k=r*sin(phi), l), r=0,
> right)=simplify(limit(subs(h=r*cos(phi),
> k=r*sin(phi), l), r=0, right));
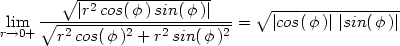
Výsledek závisí na  a uvažovaná limita tedy neexistuje, proto
f není
v bodě [0,0]
diferencovatelná.
a uvažovaná limita tedy neexistuje, proto
f není
v bodě [0,0]
diferencovatelná.
Příklad 13.6. Funkce
![{ --xy- f (x,y) = x2+y2, [x,y] ⁄= [0,0], 0, [x,y] = [0,0]](diferencialni-pocet1343x.png)
má v bodě
[0,0] obě
parciální derivace rovny nule, neboť
> f:=(x,y)-> if x=0 and y=0 then 0
> else x*y/(x^2+y^2) fi:
> limit((f(x,0)-f(0,0))/(x-0), x=0);
> limit((f(0,y)-f(0,0))/(y-0), y=0);
Jak jsme ukázali v kapitole Limita funkce,
f nemá v bodě [0,0]
limitu, a proto zde nemůže být diferencovatelná (obr. 11.4
).
Opět musíme dávat pozor na nesprávnou
interpretaci PC-grafu! Generujme PC-graf funkce
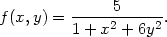
> f:=(x,y)->5/(1+x^2+6*y^2);
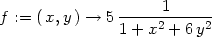
> plot3d(f(x,y), x=-2..2, y=-2..2, orientation=[13,66],
> axes=framed, shading=none, labels=[x,y,’z’]);
Získaný PC-graf (obr. 13.5) svádí
k domněnce, že funkce f
není v bodě [0,0]
diferencovatelná. Ověřme spojitost parciálních derivací v bodě
[0,0]:
> fx:=D[1](f);
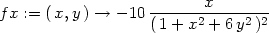
> fx(0,0);
> limit(fx(x,y), {x=0, y=0});
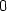
> fy:=D[2](f);
> fy(0,0);
> limit(fy(x,y), {x=0,y=0});
Funkční hodnota v bodě [0,0]
funkce fx(x,y) je
rovna limitě fx v bodě [0,0],
tedy parciální derivace fx
v bodě [0,0] je
spojitá. Totéž platí i pro fy.
Obě parciální derivace jsou v bodě [0,0]
spojité a funkce f(x,y) je
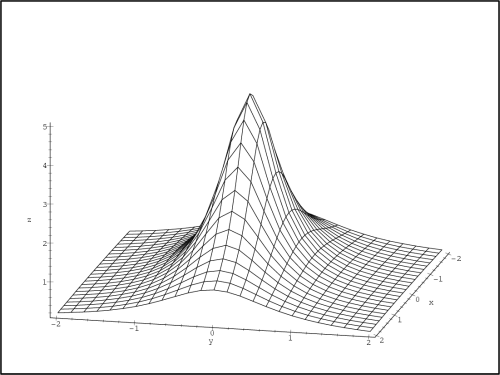
tedy v tomto bodě diferencovatelná. Generujme znovu PC-graf
funkce f, tentokrát ale pro
x 
 −0.1,0.1
−0.1,0.1 ,
y
,
y 
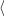 −0.1,0.1
−0.1,0.1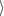 :
:
> plot3d(f(x,y), x=-0.1..0.1, y=-0.1..0.1,
> grid=[21,19], orientation=[13,66], axes=framed,
> shading=none, labels=[x,y,’z’]);
Výsledný PC-graf (obr. 13.6) lépe ilustruje
chování funkce f
v okolí bodu [0,0].
Diferenciál
Při procvičování výpočtu diferenciálu můžeme
využít i výpočetních a programovacích možností Maplu. Těchto
využijeme zejména při výpočtech diferenciálů vyšších řádů.
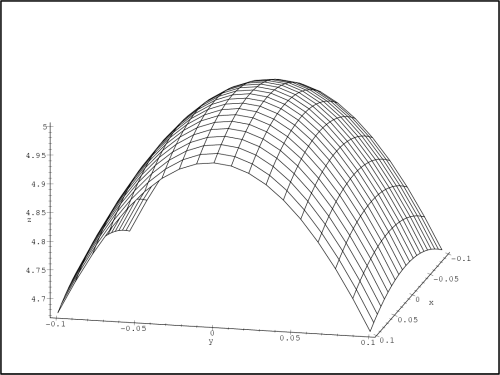
Příklad 13.7. Napište proceduru, která pro
zadanou funkci spočítá její diferenciál. Pomocí této procedury
určete diferenciál funkce f(x,y) =
x3 +
ln(xy)
nejprve v obecném bodě a poté v bodě [1,3]
s diferencemi h
= 0.2,
k = −0.01.
> difer:=proc()
>
> local derx,dery,dif;
>
> if nargs=1 then
> print(diff(args[1],x)*h+diff(args[1],y)*k);
> fi;
> if nargs=5 then
> derx:=subs(x=args[2],y=args[3],diff(args[1],x));
> dery:=subs(x=args[2],y=args[3],diff(args[1],y));
> dif:=derx*args[4]+dery*args[5];
> RETURN(dif);
> fi;
> if nargs<>1 and nargs <>5 then print
> (’Spatne_zadano’)
> fi;
> end:
Procedura difer má proměnlivý počet
argumentů. Příkaz difer(f(x,y));
určuje totální diferenciál zadané funkce v obecném bodě,
příkaz difer(f(x,y),x0,y0,h,k); totální
diferenciál dané funkce v bodě [x0,y0]
s diferencemi h, k:
> f:=(x,y)->x^3+ln(x*y);
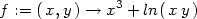
> difer(f(x,y));
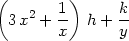
> difer (f(x,y),1,3,0.2,-0.01);

Příklad 13.8. Napište proceduru, která
počítá diferenciál m–tého řádu
funkce f. Pomocí této procedury
poté určete d2f pro
f(x,y) =
y∕x a obecně diferenciál
3. řádu libovolné funkce f.
> difern:=proc(funkce,m)
> local j;
> RETURN(sum(binomial(m,j)*
> diff(funkce, x$j,y$(m-j))*h^j*k^(m-j), j=0..m));
> end:
> difern(y/x,2);
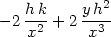
> difern(f(x,y),3);
13.2 Tečná rovina ke grafu
funkce
V této části využijeme grafické i výpočetní
možnosti Maplu k ilustraci geometrického významu totálního
diferenciálu. Vlastní generování PC-grafu je opět vhodným cvičením,
zde uvádíme dvě řešení postupná (student příklad řeší stejně jako
pomocí tužky a papíru, jen k zápisu a výpočtům používá
prostředí Maplu) a nově naprogramovanou funkci GraphTan. Uvádíme také dva
přístupy ke konstrukci tečné roviny, příklad 13.9 ilustruje spíše
analytický a příklad 13.10
spíše geometrický přístup ke
konstrukci.
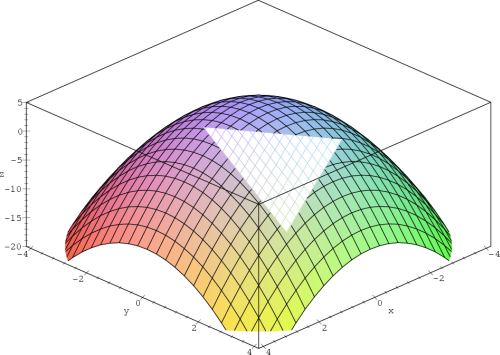
Příklad 13.9. Určete rovnici tečné roviny funkce f(x,y) = 4
− x2
− y2
v bodě [3,2].
Tečnou rovinu a funkci zakreslete do jednoho PC-grafu.
Rovnice tečné roviny funkce z
= f(x,y)
v bodě [x0,y0] má
tvar
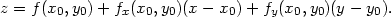
Dosaďme do tohoto vztahu:
> f:=(x,y)->4-x^2-y^2;
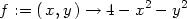
> fx(3,2):=subs(x=3,y=2, diff(f(x,y),x));
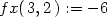
> fy(3,2):=subs(x=3,y=2, diff(f(x,y),y));
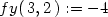
> TRovina:=(x,y)->f(3,2)+fx(3,2)*(x-3)+fy(3,2)*(y-2);
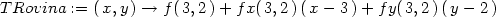
> TRovina(x,y);
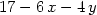
Nyní do jednoho PC-grafu umístíme společně funkci
f a její tečnou rovinu:
> P1:=plot3d(f(x,y), x=-4..4, y=-4..4, style=patch):
> P2:=plot3d(TRovina(x,y), x=-2..2,y=-2..3):
> with(plots):
> display3d({P1,P2}, axes=boxed, view=-20..30,
> labels=[x,y,’z’]);
Na základě předchozího postupu je možno řešit
úlohu: Najděte rovnici tečné roviny pro danou funkci a daný bod a
zobrazte do jednoho PC-grafu tečnou rovinu společně s funkcí
pomocí Mapleovského programovacího jazyku.
> GraphTan := proc(f,xrange,yrange,pt)
>
> #definice lokalnich promennych
> local xmin,xmax,ymin,ymax,x0,y0,z0,dx,dy,xsour,ysour,
> tanfunc,gpha,gphb,tanpt,optio,rovnice;
>
> #Vyvolani nekterych prikazu z~knihovny plots
> with(plots,pointplot):
> with(plots,display):
>
> #Ziskani ruznych promennych ze vstupu
> #Souradnice bodu dotyku
> x0 := op(2,pt)[1]:
> y0 := op(2,pt)[2]:
> #Rozsah souradnic pro vykresleni grafu
> xmin := op(1,op(2,xrange)):
> xmax := op(2,op(2,xrange)):
> ymin := op(1,op(2,yrange)):
> ymax := op(2,op(2,yrange)):
> #Parametry pro vykresleni grafu
> optio:=args[5..nargs];
>
> #Vypocet parcialnich derivaci podle x a y
> #v bode (x0,y0)
> dx := subs(x=x0,y=y0,diff(f,x)):
> dy := subs(x=x0,y=y0,diff(f,y)):
>
> #Vypocet treti souradnice bodu dotyku
> z0 := subs(x=x0,y=y0,f):
>
> #Dosazeni do rovnice pro tecnou rovinu
> tanfunc:=z0+dx*(x-x0)+dy*(y-y0):
>
> #Pojmenovani grafu bodu dotyku jako tanpt,
> #grafu funkce jako gpha a
> #grafu tecne roviny jako gphb
> tanpt:=pointplot({[x0,y0,z0]},color=red):
> gpha := plot3d(f,xrange,yrange,optio):
> xsour:=abs(xmax-xmin)/4;
> ysour:=abs(ymax-ymin)/4;
> gphb:=plot3d(tanfunc,x=x0-xsour..x0+xsour,
> y=y0-ysour..y0+ysour,optio):
>
> #Vypis vysledku
> rovnice:=z=tanfunc:
> print(‘Tecna rovina ma rovnici ‘);
> print(rovnice);
>
> #Zobrazeni grafu plochy, tecne roviny a bodu dotyku
> display ([gpha, gphb,tanpt]);
> end:
Proceduru voláme příkazem: GraphTan(funkce, x=a..b,
y=c..d, bod=[x0,y0],
volitelne_parametry); kde [x0,y0] jsou
souřadnice bodu, ve kterém tečnou rovinu počítáme (funkce musí být
v tomto bodě diferencovatelná).
Nyní řešme předcházejí příklad pomocí této nové
procedury:
> with(mvcalp):
> GraphTan(f(x,y),x=-4..4,y=-4..4,bod=[3,2],axes=boxed,
> labels=[x,y,’z’]);
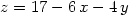
Jiný přístup ke konstrukci tečné roviny
(s využitím normály) ilustruje následující příklad:
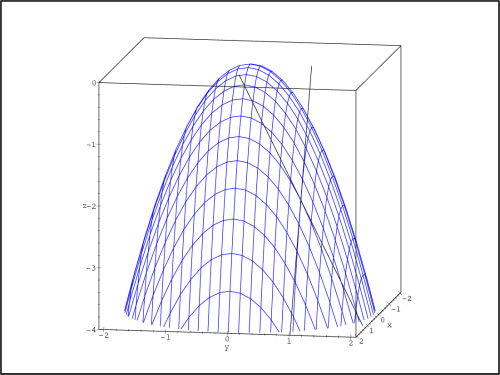
Příklad 13.10. Uvažujte funkci f(x,y) =
−(x2
+ y2) a určete
rovnici tečné roviny v bodě [−1,1].
> f:=(x,y)->-(x^2+y^2);
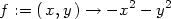
> a:=1; b:=1;
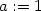
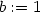
> K:=plot3d(f(x,y),x=-2..2,y=-2..2,axes=boxed,
> color=blue):
Sestrojme přímky L1 a
L2, které jsou tečnami ke grafu funkce
v bodě [−1,1]
(obr. 13.9
):
> with(plots):
> dfdx:=subs({x=a,y=b},diff(f(x,y),x));
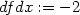
> L1:=t->[a+t,b,f(a,b)+t*dfdx];
![L1 := t → [a+ t,b,f(a,b )+ tdfdx ]](diferencialni-pocet1375x.png)
> J1:=spacecurve(L1(t),t=-3/2..1,axes=boxed,
> color=black):
> dfdy:=subs({x=a,y=b},diff(f(x,y),y));
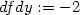
> L2:=t->[a,b+t,f(a,b)+t*dfdy];
![L2 := t → [a,b+ t,f(a,b )+ tdfdy ]](diferencialni-pocet1377x.png)
> J2:=spacecurve(L2(t),t=-3/2..1,axes=NORMAL,
> color=black):
> display3d({J1,J2,K},orientation=[10,80],
> scaling=constrained, view=-4..0, labels=[x,y,’z’]);
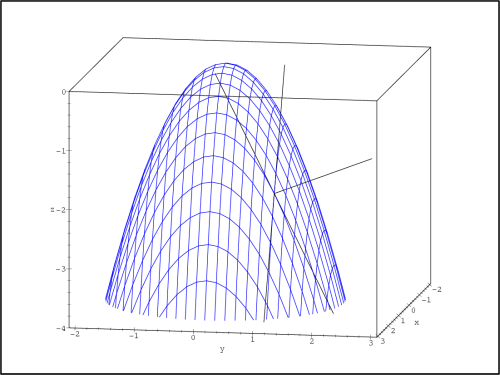
Normálový vektor v bodě [−1,1]
určíme jako vektorový součin směrových vektorů přímek L1 a
L2 (obr. 13.10
):
> with(linalg):
> N:=crossprod(L1(1)-L1(0),L2(1)-L2(0));
![N := [2 21 ]](diferencialni-pocet1378x.png)
> PL:=t->[a+t*N[1], b+t*N[2], f(a,b)+t*N[3]];
![P L := t → [a + tN1, b+ tN2, f(a,b) + tN3]](diferencialni-pocet1379x.png)
> NL:=spacecurve(PL(t),t=-3/2..1,color=black):
> display({J1,J2,K,NL}, orientation=[10,80],axes=boxed,
> scaling=constrained, view=-4..0, labels=[x,y,’z’]);
Skutečnost, že normálový vektor je kolmý na obě
přímky, ověřme pomocí skalárního součinu:
> dotprod(L1(t)-L1(0),N); dotprod(L2(t)-L2(0),N);
Rovnici tečné roviny dostáváme tak, že položíme
skalární součin vektoru [x
− a,y −
b,z − f(a,b)]
a normálového vektoru N roven nule (obr. 13.11).
> tangenteqn:=dotprod([x-a,y-b,z-f(a,b)],N)=0;
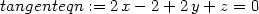
> Z:=solve(tangenteqn,z);
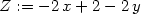
> Plane:=plot3d(Z,x=a-1/2..a+1/2,y=b-1/2..b+1/2,
> axes=boxed,color=RED,style=PATCH):
> display({Plane,K},orientation=[10,80],
> labels=[x,y,’z’]);
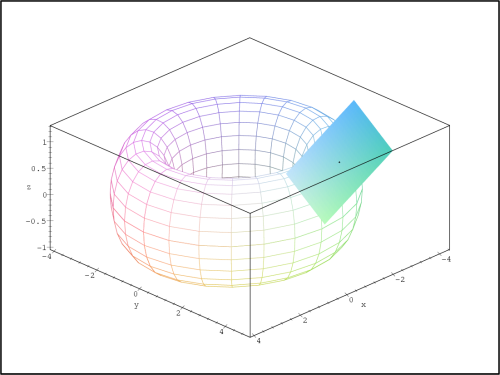
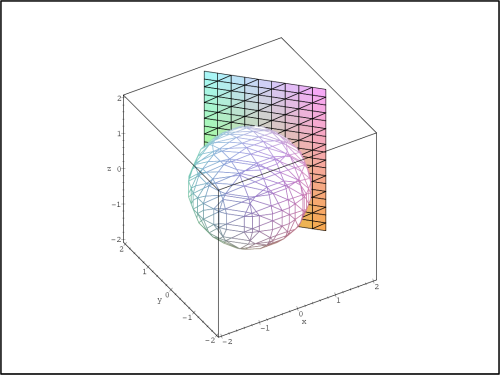
Poznámka 13.1. Pomocí Maplu můžeme konstruovat tečné roviny i
k plochám daným parametricky a implicitně. Pro generování
PC-grafů použijeme naprogramovaných procedur ParamTan a ImplicitTan. Obě procedury jsou
uloženy v knihovně mvcalp:
> ParamTan([(3+cos(s))*cos(t), (3+cos(s))*sin(t),
> sin(s)], s=0..2*Pi, t=0..2*Pi, point=[1,2]);
> ImplicitTan(x^2+y^2+z^2=2, x=-2..2, y=-2..2, z=-2..2,
> point=[1,1,0], style=patch, orientation=[-121,53],
> scaling=constrained, labels=[x,y,’z’]);
Na obrázku 13.12
je anuloid daný parametricky
rovnicemi x = (3+coss)cost,
y =
(3 + coss)sint,
z = sins a
jeho tečná rovina v bodě [1,2], na
obrázku 13.13
koule daná implicitně rovnicí
x2 +
y2 +
z2 = 2 a
její tečná rovina v bodě [1,1].
13.3 Užití diferenciálu
k přibližným výpočtům
Nyní použijeme počítačového systému i
k procvičování přibližných výpočtů pomocí totálního
diferenciálu. Rovnice tečné roviny je nejlepší lineární aproximací
funkce f(x,y)
v okolí bodu [x0,y0].
Uvažujme chybu této aproximace
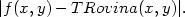 Nechť f(x,y) = 4
− x2
− y2
(příklad 4.9) a nechť [x,
y] nabývá postupně hodnot
[4,3],
[3.8,2.8],
[3.6,2.6],
[3.4,2.4],
[3.2,2.2] a
[3,2].
Nechť f(x,y) = 4
− x2
− y2
(příklad 4.9) a nechť [x,
y] nabývá postupně hodnot
[4,3],
[3.8,2.8],
[3.6,2.6],
[3.4,2.4],
[3.2,2.2] a
[3,2].
Pomocí příkazu seq pozorujeme, jak se chyba
aproximace zmenšuje s hodnotami blížícími se bodu [3,2]:
> seq(evalf(abs(f(4-i/5, 3-i/5)-
> TRovina(4-i/5, 3-i/5))), i=0..5);
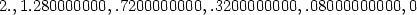
Jiný způsob řešení je možný pomocí příkazu
zip:
> zip((x,y)->abs(f(x,y)-TRovina(x,y)),
> [4,3.8,3.6,3.4,3.2,3], [3,2.8,2.6,2.4,2.2,2]);
![[2,1.28,.72,.32,.08,0]](diferencialni-pocet1391x.png)
K nalezení lineární aproximace funkce je
možno použít i Taylorova polynomu, neboť diferenciál funkce je
Taylorovým polynomem stupně 1 (Taylorův polynom viz kapitola
Derivace složené funkce, Taylorův vzorec). Následující příkazy
ilustrují použití příkazu mtaylor
k nalezení lineární aproximace:
> readlib(mtaylor);
proc() ... end
> mtaylor(f(x,y), [x=3,y=2], 2);
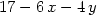
Příklad 13.11. Pomocí totálního
diferenciálu přibližně vypočtěte ln(2.12
+ 0.92).
Určíme bod [x0,y0],
diference dx a dy a najdeme funkci f(x,y)
takovou, aby
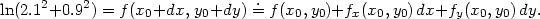
K výpočtu tedy použijeme funkci
f(x,y) =
ln(x2
+ y2), bod
[2,1] a
diference
dx = 0.1,
dy = −0.1:
> f:=(x,y)->ln(x^2+y^2);
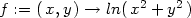
> x0:=2:y0:=1:dx:=1/10:dy:=-1/10:
Spočtěme diferenciál funkce f(x,y):
> A:=D[1](f);
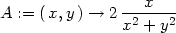
> B:=D[2](f);
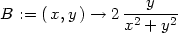
> df:=(x,y)->A(x,y)*dx+B(x,y)*dy;
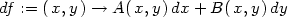
> priblizna_hodnota:=f(x0,y0)+df(x0,y0);
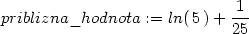
> evalf(priblizna_hodnota);
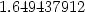
Předchozí výsledek nyní ověřme přímým výpočtem
(Maple umožňuje provádět výpočty v oboru reálných čísel
s téměř libovolnou přesností):
> funkcni_hodnota:=f(x0+dx,y0+dy);
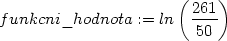
> evalf(funkcni_hodnota);
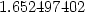
K výpočtu můžeme použít i procedury
difer:
> with(mvcalp):
> f(x0,y0)+difer(f(x,y),x0,y0,dx,dy);
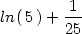
> evalf(");

13.4 Taylorova věta
K hledání Taylorova polynomu funkce dvou
proměnných používáme v Maplu proceduru mtaylor.
Příklad 13.12. Najděte Taylorův polynom
2. stupně se středem v bodě [0,0] pro
funkci f(x,y) =
sinxcosy.
Proceduru mtaylor si zpřístupníme pomocí
readlib:
> readlib(mtaylor):
Definujme funkci f a Taylorův polynom 2. stupně uložme
do proměnné f2:
> f:=(x,y)->sin(x)*sin(y);
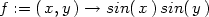
> f2:=mtaylor(f(x,y), [x=0,y=0], 3);

Nyní zkonvertujme f2 na
funkci pomocí příkazu unapply:
> f2:=unapply(f2,x,y);
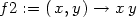
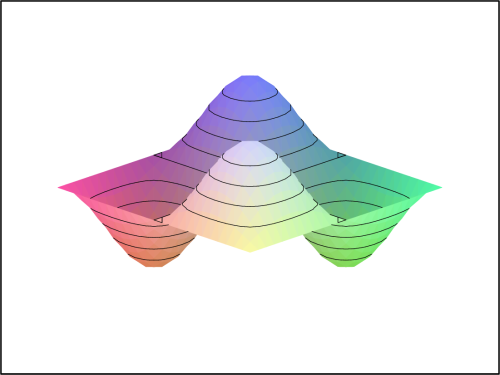
a generujme postupně PC-grafy pro
funkci f
(obr. 13.14
), její Taylorův polynom 2. stupně
(obr. 13.15
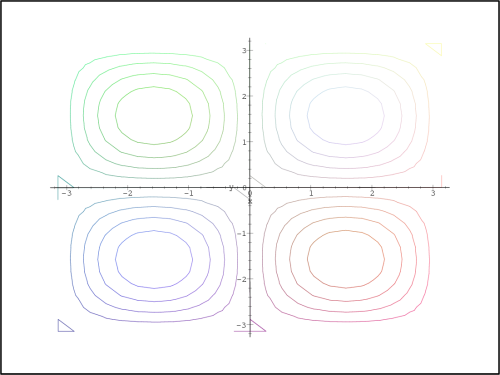
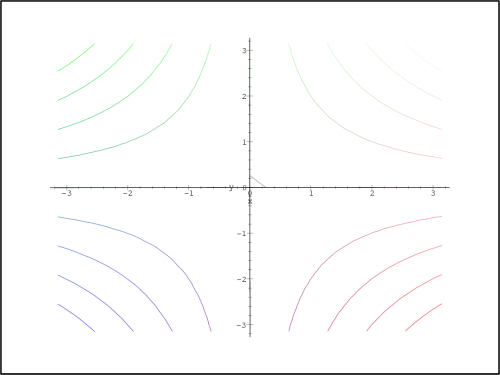
), vrstevnice funkce f (obr. 13.16
) a vrstevnice T2(x,y)
(obr. 13.17
).
> P1:=plot3d(f(x,y), x=-Pi..Pi, y=-Pi..Pi,
> orientation=[45,60], style=patchcontour):";
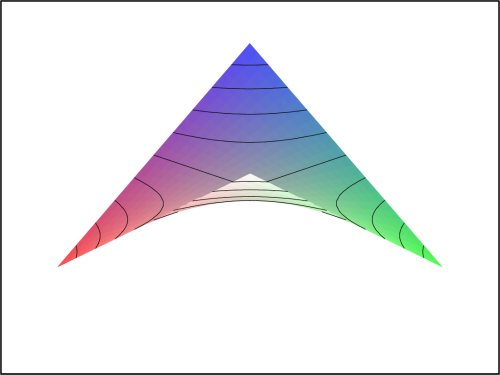
> P2:=plot3d(f2(x,y), x=-Pi..Pi, y=-Pi..Pi,
> orientation=[45,60], style=patchcontour):";
> plot3d(f(x,y), x=-Pi..Pi, y=-Pi..Pi,
> orientation=[270,0], axes=normal, style=contour);
> plot3d(f2(x,y), x=-Pi..Pi, y=-Pi..Pi,
> orientation=[270,0], axes=normal, style=contour);
Další PC-grafy znározňují funkci a její Taylorův
polynom nad čtvercem [−0.5,0.5]
 [−0.5,0.5],
tedy v blízkém okolí bodu [0,0]
(obr. 13.18
) a nad čtvercem [−p,
p]
[−0.5,0.5],
tedy v blízkém okolí bodu [0,0]
(obr. 13.18
) a nad čtvercem [−p,
p]  [−p,
p] (obr. 13.19
).
[−p,
p] (obr. 13.19
).
> plots[display]({P1,P2}, axes=framed,
> view=[-.5..0.5,-.5..0.5,-1..1], labels=[x,y,’z’]);
> plots[display]({P1,P2},orientation=[71,63],
> axes=framed, labels=[x,y,’z’]);
Všimněme si, že v blízkém okolí bodu
[0,0] se
Taylorův polynom T2(x,y)
téměř shoduje s funkcí f
(obr. 13.18
).
Tuto skutečnost ilustrujme dále PC-grafy
(obr. 13.20
a 13.21
) znázorňujícími závislost chyby, které
se dopustíme při aproximaci funkce f v okolí bodu [0,0]
Taylorovým polynomem 2. stupně, na vzdálenosti od tohoto
bodu:
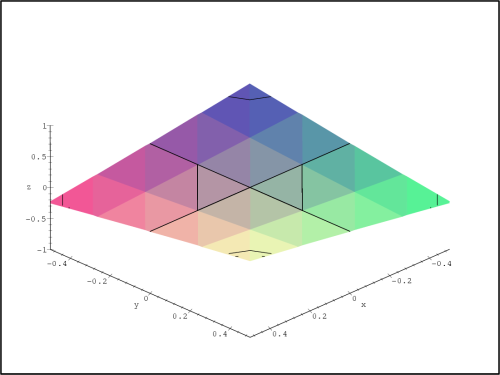
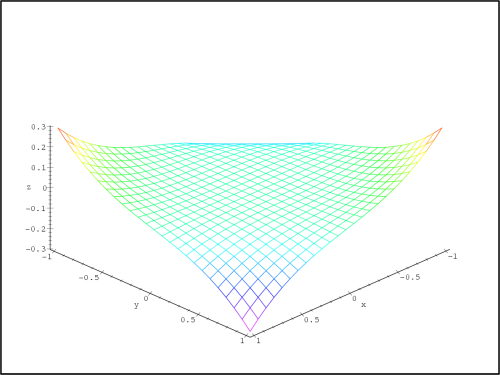
> plot3d(f(x,y)-f2(x,y),x=-.5..0.5,y=-.5..0.5,
> axes=framed,shading=zhue,labels=[x,y,’z’]);
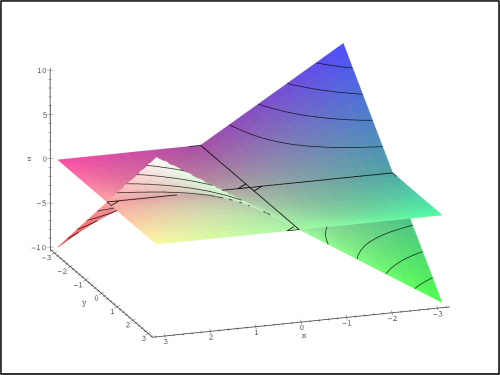
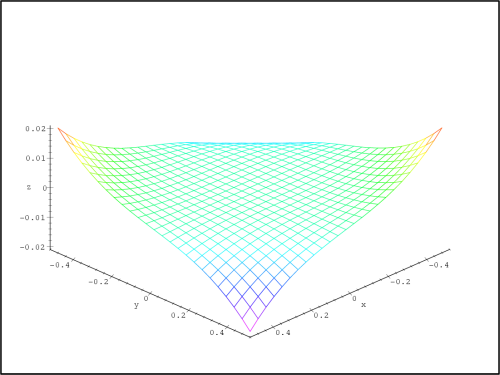
> plot3d(f(x,y)-f2(x,y), x=-1..1, y=-1..1,
> axes=framed, shading=zhue,labels=[x,y,’z’]);
Na obrázku 13.20
je chyba znázorněna nad čtvercem
[−0.5,0.5] [−0.5,0.5] a na
obrázku 13.21
nad čtvercem [−1,1]
[−0.5,0.5] a na
obrázku 13.21
nad čtvercem [−1,1]
 [−1,1].
Z PC-grafů je vidět, že pokud zvětšujeme vzdálenost od bodu
[0,0],
zvětšuje se i chyba aproximace.
[−1,1].
Z PC-grafů je vidět, že pokud zvětšujeme vzdálenost od bodu
[0,0],
zvětšuje se i chyba aproximace.
Při použití procedury mtaylor však zůstává Taylorův
vzorec „skryt uvnitř procedury“. Maplu proto použijeme nyní i
k procvičování výpočtů Taylorova polynomu a dále
k přibližným výpočtům funkčních hodnot funkcí dvou
proměnných.
Příklad 13.13. Určete Taylorův polynom
2. stupně se středem v bodě [x0,y0] =
[1,1] pro funkci f(x,y) =
x∕y.
Příklad řešme postupně. Maple nám nejdříve pouze asistuje při
výpočtu parciálních derivací a výsledek až nakonec ověříme pomocí
procedury mtaylor.
Spočtěme tedy všechny potřebné parciální
derivace:
> f:=(x,y)->x/y;
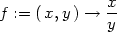
> fx:=D[1](f);fy:=D[2](f);
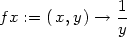
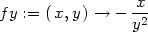
> fxx:=D[1,1](f);fxy:=D[1,2](f);fyy:=D[2,2](f);
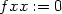
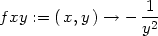
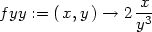
Podle Věty 5.4
platí:
> T2:=f(1,1)+fx(1,1)*(x-1)+fy(1,1)*(y-1)+
> (1/2)*((fxx(1,1)*(x-1)^2+2*fxy(1,1)*(x-1)*(y-1)+
> fyy(1,1)*(y-1)^2));
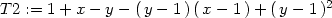
> T2:=expand(T2);

Nyní ověřme výsledek pomocí procedury mtaylor:
> readlib(mtaylor):
> T2:=mtaylor(f(x,y), [x=1,y=1],3);
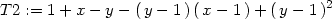
> T2:=expand(");

V obou případech jsme dostali stejný
výsledek, T2(x,y) =
1+2x−2y−xy
+y2.
Příklad 13.14. Pomocí Taylorova polynomu 2.
stupně určete přibližně
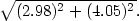
K výpočtu využijme Taylorova polynomu 2. stupně funkce
f(x,y) =
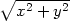
v bodě
[x0,y0] =
[3,4]:
> f:=(x,y)->sqrt(x^2+y^2);
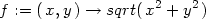
> f2:=mtaylor(f(x,y), [x=3,y=4], 3);
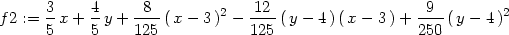
> f2:=unapply(f2,x,y);
> aprox2:=f2(2.98,4.05);
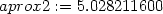
Funkční hodnotu můžeme v Maplu určit i přímým
výpočtem:
> sk:=f(2.98,4.05);

Závěrem určeme chybu aproximace:
> chyba:=sk-aprox2;
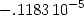
K aproximaci použijme nyní Taylorova polynomu
6. stupně a opět určeme chybu aproximace:
> f6:=mtaylor(f(x,y), [x=3,y=4], 7):
> f6:=unapply(f6,x,y): aprox6:=f6(2.98,4.05);
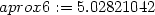
> sk:=f(2.98,4.05);
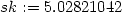
> chyba2:=sk-aprox6;
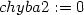
Standardní nastavení přesnosti aproximativní
aritmetiky v Maplu je na 9 platných míst. Protože rozdíl je až
v řádu 10−15, dostáváme při
této přesnosti výpočtu chybu rovnu nule. Zvyšme tedy přesnost
aproximativní aritmetiky a výpočet proveďme znovu.
> Digits:=17;
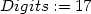
> aprox6:=f6(2.98,4.05);
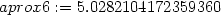
> sk:=f(2.98,4.05);
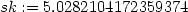
> chyba2:=sk-aprox6;
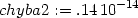
Z výsledků je vidět, že s rostoucím
stupněm Taylorova polynomu se zmenšuje chyba aproximace.
13.5 Kmenová funkce
Hledat kmenovou funkci můžeme taktéž pomocí
příkazů Maplu. Uvádíme nejdříve řešení postupně po jednotlivých
krocích, v závěru je pak příklad řešen pomocí Mapleovského
programovacího jazyka.
Příklad 13.15. Rozhodněte, zda je výraz
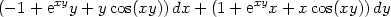
diferenciálem nějaké funkce; v případě že ano, určete tuto
funkci.
> m:=(x,y)->-1+exp(x*y)*y+y*cos(x*y);
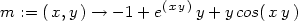
> n:=(x,y)->1+exp(x*y)*x+x*cos(x*y);
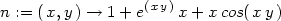
> m(x,y)*dx+n(x,y)*dy;
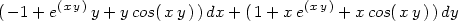
Nejprve ověřme, zda je zadaný výraz opravdu
diferenciálem:
> testeq(diff(m(x,y),y)=diff(n(x,y),x));
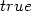
Platí

tj. zadaný výraz je diferenciálem jisté kmenové funkce
H. Dále platí:
> k1:=integrate(m(x,y),x);
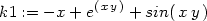
Integrační konstantu označíme g(y) (její
derivace podle x je
nulová).
Derivováním podle y:
> k2:=diff(k1+g(y),y);
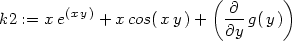
a dosazením do vztahu Hy
= n(x,y)
dostáváme:
> k3:=solve(k2=n(x,y), diff(g(y),y));
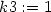
Odtud g (y) = 1 a
g(y) =
y + c.
(y) = 1 a
g(y) =
y + c.
> k4:=integrate(k3,y);
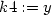
> reseni:=k1+k4;
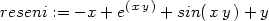
Zadaný výraz je tedy diferenciálem funkce
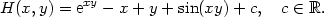
Příklad 13.16. Napište proceduru, která
určí, zda je zadaný výraz diferenciálem nějaké funkce a
v případě, že ano, tuto funkci určí.
> kmen:=proc(m,n)
> if diff(m,y)=diff(n,x) then
> simplify(integrate(m,x)+
> integrate(n-diff(integrate(m,x),y),y));
> else print(‘Zadany vyraz neni diferencialem
> zadne funkce‘);
> fi
> end:
Pomocí této procedury nyní určeme kmenovou
funkci pro výraz (x2
− y2)dx
+ (5 − 2xy)dy:
> n:=(x,y)->5-2*x*y;
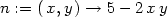
> m:=(x,y)->x^2-y^2;
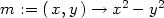
> kmen(m(x,y),n(x,y));
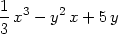
Vypočítali jsme, že zadaný výraz je diferenciálem
funkce
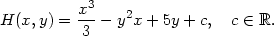
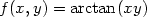
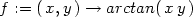
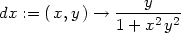
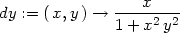
 (0,0)
(0,0)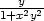 a lim(x,y)
a lim(x,y)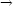 (0,0)
(0,0)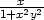 určíme dosazením
souřadnic limitního bodu:
určíme dosazením
souřadnic limitního bodu:
![{ -x2y-, [x,y] ⁄= [0,0], f (x,y) = x2+y2 0, [x,y] = [0,0]](diferencialni-pocet1316x.png)
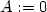
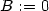
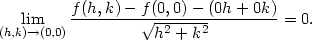
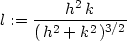
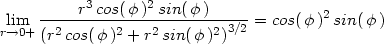

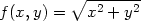
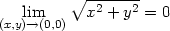
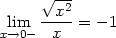
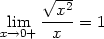
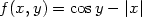
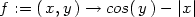
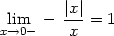
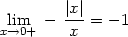
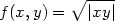
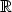
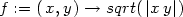
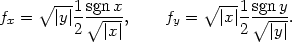
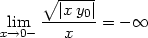
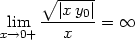
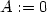
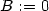
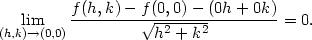
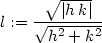
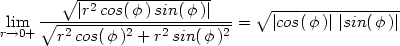
![{ --xy- f (x,y) = x2+y2, [x,y] ⁄= [0,0], 0, [x,y] = [0,0]](diferencialni-pocet1343x.png)
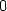
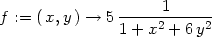
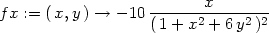
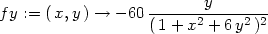

 −
−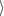
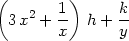

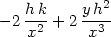
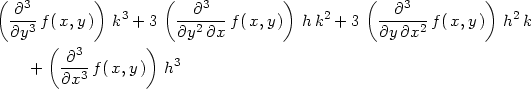
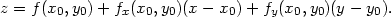
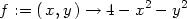
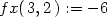
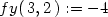
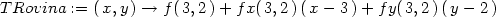
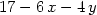
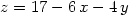
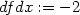
![L1 := t → [a+ t,b,f(a,b )+ tdfdx ]](diferencialni-pocet1375x.png)
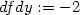
![L2 := t → [a,b+ t,f(a,b )+ tdfdy ]](diferencialni-pocet1377x.png)
![N := [2 21 ]](diferencialni-pocet1378x.png)
![P L := t → [a + tN1, b+ tN2, f(a,b) + tN3]](diferencialni-pocet1379x.png)
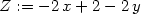
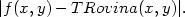
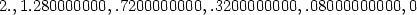
![[2,1.28,.72,.32,.08,0]](diferencialni-pocet1391x.png)
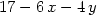
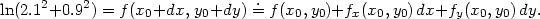
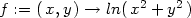
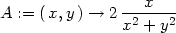
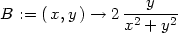
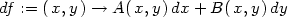
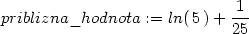
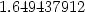
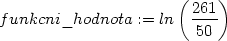
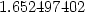
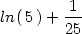

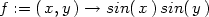

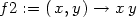

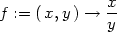
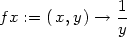
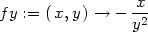
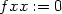
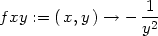
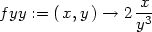
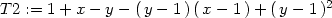

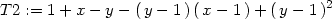

 v bodě
v bodě