 (x0) =
f
(x0) =
f (u0)g
(u0)g (x0).
(x0).[Další] [Předchozí] [Předchozí – na konec] [Na konec] [Výše]
Stejně jako u funkce jedné proměnné potřebujeme u funkcí více proměnných určit parciální derivace složené funkce. To je obsahem prvního odstavce, kde také ukážeme použití odvozených vzorců. Druhý odstavec této kapitoly je věnován Taylorovu vzorci pro funkci více proměnných. Podrobnější srovnání s funkcí jedné proměnné provedeme v každém odstavci zvlášť.
Vzorce pro parciální derivace složených funkcí jsou jedním z nejdůležitějších nástrojů řešení rovnic matematické fyziky. Tyto rovnice jsou tzv. parciální diferenciální rovnice – to jsou rovnice, které obsahují parciální derivace neznámé funkce a jejichž řešení jsou funkce dvou či více proměnných. Odvozené vzorce umožňují transformovat tyto rovnice na jednodušší tvar, z něhož buď již umíme najít řešení, nebo alespoň můžeme vyvodit řadu důležitých vlastností řešení rovnice.
Na úvod připomeňme, jak se derivuje složená
funkce jedné proměnné. Nechť funkce u =
g(x) má
derivaci v bodě x0.
Označme u0 =
g(x0). Má-li
funkce y = f(u)
derivaci v bodě u0,
pak složená funkce y
= F(x) =
f(g(x)) má
derivaci v bodě x0 a
platí: y (x0) =
f
(x0) =
f (u0)g
(u0)g (x0).
(x0).
Nyní odvodíme podobné vztahy pro parciální derivace složené funkce dvou proměnných. Bude nás především zajímat případ, kdy vnější funkce f není explicitně zadána (obvykle je to hledané řešení parciální diferenciální rovnice).
Věta 5.1. Nechť funkce u = u(x,y), v = v(x,y) mají parciální derivace prvního řádu v bodě [x0,y0], označme u0 = u(x0,y0), v0 = v(x0,y0). Je-li funkce z = f(u,v) diferencovatelná v bodě [u0,v0], pak složená funkce z = F(x,y) = f(u(x,y),v(x,y)) má parciální derivace 1. řádu v bodě [x0,y0] a platí:
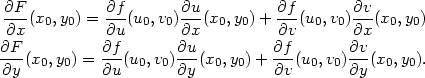 |
(5.1) |
Zkráceně píšeme
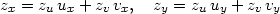 |
(5.2) |
nebo také
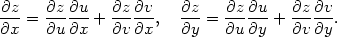 |
(5.3) |
Důkaz. Dokážeme pouze první vzorec v (5.1 ), druhý se dokáže zcela analogicky. Vyjdeme přímo z definice parciální derivace.
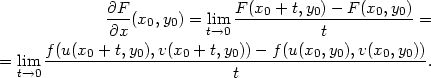 |
(5.4) |
Označíme-li u(t) =
u(x0
+ t,y0),
v(t) =
v(x0
+ t,y0),
z diferencovatelnosti funkce f plyne existence funkce  splňující (4.3) takové, že
splňující (4.3) takové, že
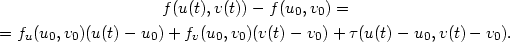
|
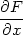 (x0,y0) =
limt (x0,y0) =
limt 0 0  |
|||
![+ τ(u(t) − u0,v(t) − v0)]](diferencialni-pocet425x.png) = fu(u0,v0)limt
= fu(u0,v0)limt 0 0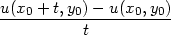 + + |
|||
+
fv(u0,v0)limt 0 0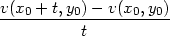 + limt + limt 0 0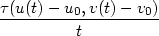 = = |
|||
=
fu(u0,v0)ux(x0,y0) +
fv(u0,v0)vx(x0,y0) +
limt 0 0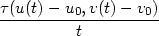 . . |
limt 0 0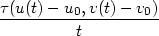 = limt = limt 0 0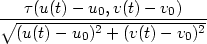  |
|||
 |
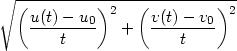 = = |
||
=
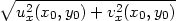
 limt limt 0 0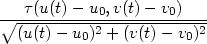 =
0. =
0. |
 0u(t) =
u0,limt
0u(t) =
u0,limt 0v(t) =
v0, neboť funkce u(t) =
u(x0
+ t,y0),v(t) =
v(x0
+ t,y0) jsou
spojité v bodě t
= 0 – to plyne
z existencí parciálních derivací funkcí u,v v bodě t = 0 a
pro funkci jedné proměnné plyne z existence derivace
spojitost. □
0v(t) =
v0, neboť funkce u(t) =
u(x0
+ t,y0),v(t) =
v(x0
+ t,y0) jsou
spojité v bodě t
= 0 – to plyne
z existencí parciálních derivací funkcí u,v v bodě t = 0 a
pro funkci jedné proměnné plyne z existence derivace
spojitost. □
Příklad 5.1. i) Je dána funkce z = eu sinv, kde u = xy a v = x + y. Vypočtěte zx a zy.
Řešení. Protože vnitřní i vnější složky mají spojité
parciální derivace v celém  2, má
složená funkce parciální derivace v každém bodě tohoto
prostoru. Dosazením do (5.2
) dostáváme
2, má
složená funkce parciální derivace v každém bodě tohoto
prostoru. Dosazením do (5.2
) dostáváme
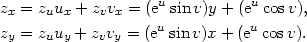
|

ii) Pomocí transformace do nových nezávisle
proměnných u = x
+ y, v = x
− y najděte všechny diferencovatelné funkce
f :  2
2

 splňující rovnost
splňující rovnost
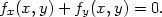 |
(5.5) |
Řešení. Označme z = f(x,y). Pak zx = zuux + zvvx = zu + zv, zy = zuuy + zvvy = zu −zv. Dosazením dostáváme zu + zv + zu −zv = 2zu = 0, tedy zu = 0. To znamená, že funkce z = z(u,v) nezávisí na proměnné u, a tedy z(u,v) = g(v), kde g je libovolná diferencovatelná funkce jedné proměnné. Dosazením za v vidíme, že všechny diferencovatelné funkce dvou proměnných, které splňují (5.5 ), jsou tvaru f(x,y) = g(x−y), kde g je libovolná diferencovatelná funkce jedné proměnné.
iii) Proveďte totéž jako v předchozím
příkladě zavedením polárních souřadnic  =
arctg
=
arctg  , r =
, r = 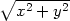 do rovnice
do rovnice
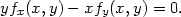 |
(5.6) |
Řešení. Vypočtěme nejprve parciální derivace funkcí
r a  :
:
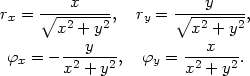
|
| zx = | zr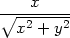 − z − z 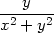 , , |
||
| zy = | zr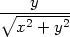 + z + z 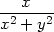 , , |
 = 0, a tedy z(r,
= 0, a tedy z(r, ) = h(r).
Všechny funkce dvou proměnných splňující rovnici (5.6) jsou tedy tvaru
f(x,y) =
h(
) = h(r).
Všechny funkce dvou proměnných splňující rovnici (5.6) jsou tedy tvaru
f(x,y) =
h(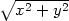 ), kde
h je libovolná diferencovatelná
funkce jedné proměnné.
), kde
h je libovolná diferencovatelná
funkce jedné proměnné.
Na předchozích příkladech vidíme, že zavedením nových nezávisle proměnných můžeme dosáhnout značného zjednodušení dané parciální diferenciální rovnice, což se velmi často využívá především při řešení diferenciálních rovnic popisujících různé fyzikální děje. Protože tyto rovnice jsou většinou 2. řádu (obsahují parciální derivace 2. řádu neznámé funkce), zvláště důležité jsou vzorce pro parciální derivace 2. řádu složených funkcí.
Dříve než si tyto vzorce pro parciální derivace
2. řádu uvedeme, připomeňme opět pro srovnání vzorec pro
derivace 2. řádu složené funkce jedné proměnné. Derivováním
rovnosti y =
f
=
f (u(x))g
(u(x))g (x)
dostáváme
(x)
dostáváme
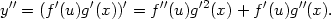
Věta 5.2. Nechť funkce u = u(x,y), v = v(x,y) mají parciální derivace 2. řádu v bodě [x0,y0], označme u0 = u(x0,y0), v0 = v(x0,y0). Má-li funkce z = f(u,v) spojité parciální derivace 2. řádu v bodě [u0,v0], pak složená funkce z = F(x,y) = f(u(x,y),v(x,y)) má parciální derivace 2. řádu v bodě [x0,y0] a platí:
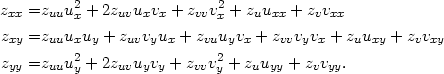 |
(5.7) |
Funkce z a její parciální derivace mají argument (u0,v0), funkce u,v a jejich parciální derivace mají argument (x0,y0).
Důkaz. Dokážeme pouze rovnost pro zxx, důkaz zbývajících dvou vzorců je zcela analogický. Platí
| zxx = | 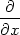 (zx) = (zx) =
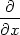 (zuux
+ zvvx) = (zuux
+ zvvx) =
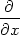 (zuux) + (zuux) +
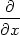 (zvvx) = (zvvx) = |
||
| = | 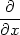 (zu)ux
+ zuuxx
+ (zu)ux
+ zuuxx
+ 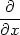 (zv)vx
+ zvvxx
= (zv)vx
+ zvvxx
= |
||
| = | (zuuux + zuvvx)ux + zuuxx + (zvuux + zvvvx)vx+ | ||
| + | zvvxx = zuuux2 + zuvvxux + zvvvx2 + zvuuxvx + zuuxx + zvvxx = | ||
| = | zuuux2 + 2zuvuxvx + zvvvx2 + zuuxx + zvvxx. |
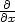 zu
a
zu
a 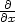 zv
jsme využili skutečnosti, že zu
= zu(u(x,y),v(x,y))
a zv =
zv(u(x,y),v(x,y))
jsou opět složené funkce proměnných x,y, a proto můžeme k výpočtu
jejich derivací využít vztahů (5.1
), ve kterých místo z dosadíme zu,
resp. zv. □
zv
jsme využili skutečnosti, že zu
= zu(u(x,y),v(x,y))
a zv =
zv(u(x,y),v(x,y))
jsou opět složené funkce proměnných x,y, a proto můžeme k výpočtu
jejich derivací využít vztahů (5.1
), ve kterých místo z dosadíme zu,
resp. zv. □
Poznámka 5.1. K zapamatování vzorců (5.7) můžeme použít formální umocnění, o kterém jsme se již zmínili u výpočtu diferenciálů vyšších řádů (Poznámka 4.5). Například pro výpočet zxx formálně umocníme pravou stranu rovnosti zx = zuux + zvvx. Dostaneme zu2ux2 + 2zuzvuxvx + zv2vx2, a nahradíme-li druhé mocniny, resp. součin prvních derivací funkce z odpovídajícími druhými derivacemi, obdržíme zuuux2+2zuvuxvx+zvvvx2, což jsou právě první tři členy v (5.7 ).
Příklad 5.2. i) Pomocí transformace do nových nezávisle proměnných u = x + ay, v = x − ay najděte obecné řešení tzv. vlnové rovnice
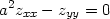
Řešení. Využitím vzorečků pro parciální derivace 1. a 2. řádu dostáváme
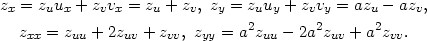
|
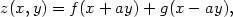
Je-li ještě zadána počáteční poloha a rychlost
chvějící se struny, tj. je daná dvojice funkcí  ,
,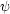 jedné proměnné popisující počáteční stav
struny, pak dvojice počátečních podmínek
jedné proměnné popisující počáteční stav
struny, pak dvojice počátečních podmínek

ii) Pomocí transformace nezávisle proměnných
u = xy, v = 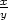 najděte všechny funkce dvou
proměnných splňující rovnici
najděte všechny funkce dvou
proměnných splňující rovnici
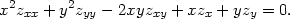

|
zuu(x2y2
+ x2y2
− 2x2y2) +
zuv(2x2
− 2x2) +
zvv(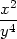 + + 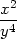 + 2 + 2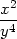 )+ )+ |
|||
+
zu(−2xy
+ xy +
xy)
+ zv( + 2 + 2 − − ) = 4 ) = 4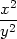 zvv
+ zvv
+  zv =
0, zv =
0, |
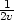 zv
= 0. Řešením této rovnice je
zv(u,v) =
zv
= 0. Řešením této rovnice je
zv(u,v) =
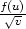 , kde f je
libovolná (diferencovatelná) funkce jedné proměnné, a odtud
z(u,v) =
2f(u)
, kde f je
libovolná (diferencovatelná) funkce jedné proměnné, a odtud
z(u,v) =
2f(u)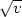 +
g(u), kde
g je libovolná funkce jedné
proměnné se spojitou druhou derivací, což po dosazení za
u,v dává
+
g(u), kde
g je libovolná funkce jedné
proměnné se spojitou druhou derivací, což po dosazení za
u,v dává
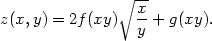
iii) Transformujte tzv. Laplaceovu rovnici1 v  2
2
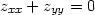
 , y = r
sin
, y = r
sin , za předpokladu, že funkce z má spojité parciální derivace
2. řádu.
, za předpokladu, že funkce z má spojité parciální derivace
2. řádu.
Řešení. Podle (5.2 ) platí
| zr | =
zx xr
+ zy
yr =
zx cos + zy
sin + zy
sin , , |
||
z |
=
zx x + zy
y + zy
y =
−zx
r sin =
−zx
r sin + zy
r cos + zy
r cos . . |
| zrr | = zxxxr2 + 2zxy xryr + zyy yr2 + zx xrr + zy yrr = | ||
=
zxx cos2 + zxy
sin2 + zxy
sin2 + zyy
sin2 + zyy
sin2 , , |
|||
z  |
=
zxxx 2
+ 2zxyx 2
+ 2zxyx y y + zyyy + zyyy 2
+ zx
z 2
+ zx
z  +
zy y +
zy y  = = |
||
=
zxxr2
sin2 − zxyr2
sin2 − zxyr2
sin2 + zyyr2
cos2 + zyyr2
cos2 − zxr
cos − zxr
cos −
zyr
sin −
zyr
sin . . |

 , dostáváme
, dostáváme
r2zrr
+ z  = r2zxx(cos2 = r2zxx(cos2 + sin2 + sin2 ) + r2zyy(cos2 ) + r2zyy(cos2 + sin2 + sin2 )+ )+ |
|||
+
zxy(sin2 − sin2 − sin2 ) −
r[zx
cos ) −
r[zx
cos +
zy sin +
zy sin ] = ] = |
|||
| = r2(zxx + zyy) − rzr. |
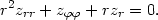
Poznámka 5.2. Ve všech řešených příkladech, které jsme zde uvedli, byla transformace do nových proměnných dána již v zadání. V rovnicích matematické fyziky se vyšetřují rovnice typu
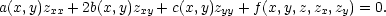
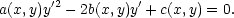
Doposud jsme uvažovali pouze funkce dvou proměnných, ale situace pro funkce více proměnných je zcela analogická, včetně důkazu následujícího tvrzení.
Věta 5.3. Nechť je
dána
funkce f :  m
m 
 a m-tice
funkcí gi
:
a m-tice
funkcí gi
:  n
n 
 ,
které mají spojité
parciální derivace
2. řádu. Označme uk
= gk(x1,…,xn),k = 1,…,m. Pak pro složenou funkci
F(x1,…,xn) = f(g1(x1…,xn),…,gm(x1,…,xn)) platí
,
které mají spojité
parciální derivace
2. řádu. Označme uk
= gk(x1,…,xn),k = 1,…,m. Pak pro složenou funkci
F(x1,…,xn) = f(g1(x1…,xn),…,gm(x1,…,xn)) platí
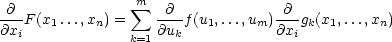 |
(5.8) |
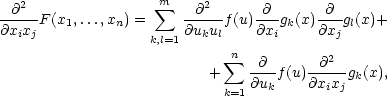 |
(5.9) |
kde i,j = 1,2,…,n a ve vzorci (5.9 ) je u = (u1…,un), x = (x1,…,xn).
Poznámka 5.3. i) Jsou-li funkce gi ve Větě 5.3 lineární, pak všechny členy v druhé sumě v (5.9) jsou nulové (neboť druhá derivace lineární funkce je nulová). Metoda formálního vynásobení derivací prvního řádu a následná náhrada součinů prvních derivací odpovídajícími druhými derivacemi pak dává přímo vztahy pro druhou derivaci. Takto je tomu např. v Příkladu 5.2 i).
ii) Uvedli jsme si zde pouze vzorce pro parciální derivace složené funkce 1. a 2. řádu, které jsou potřeba v rovnicích matematické fyziky. Metodou stejnou jako v důkazu Věty 5.2 lze odvodit vztahy pro třetí a vyšší derivace, nebudeme je zde však již uvádět, neboť jsou formálně poměrně složité.
Příklad 5.3. i)
Transformujte Laplaceovu rovnici
v  3
3
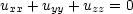
 sin
sin ,
y =
r sin
,
y =
r sin sin
sin ,
z =
r cos
,
z =
r cos .
.
Řešení. Mohli bychom
postupovat podobně
jako při řešení Příkladu 5.2 iii), zde však pro ilustraci
různých možných metod
postupujeme odlišně.
Vyjádříme nejprve
r, ,
, pomocí
x,y,z.
Jednoduchými úpravami dostáváme
pomocí
x,y,z.
Jednoduchými úpravami dostáváme
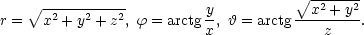
 ,
, . Platí
. Platí
rx
= 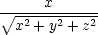 = =
 , ry
= , ry
= 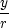 , rz
= , rz
=  , , |
|||
rxx
=  − −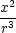 , ryy
= , ryy
=  − −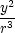 , rzz
= , rzz
=  − −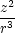 , , |
|||
 x = x = 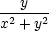 , ,  y
= − y
= −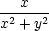 , ,  z = 0, z = 0, |
|||
 xx = xx = 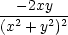 , ,  yy
= yy
= 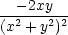 , , zz =
0, zz =
0, |
|||
 x = x = 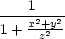 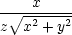 = = 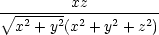 = = 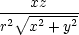 , , |
|||
 y = y = 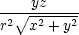 , ,  z = z = 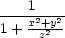 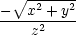 = −
= −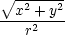 , , |
|||
 xx = xx = 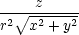 −
2 −
2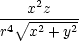 −
−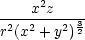 , , |
|||
 yy = yy = 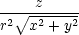 −
2 −
2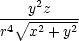 −
− , , |
|||
 zz = zz = 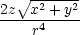 . . |
| ux | = urrx
+ u  x
+ u x
+ u  x
= ur x
= ur + u + u 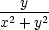 + u + u 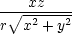 , , |
||
| uy | = ur − u − u 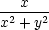 + u + u 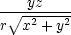 , , |
||
| uz | = ur − u − u 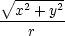 , , |
uxx
= urr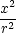 + u + u  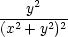 + u + u  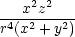 + 2ur + 2ur xyr(x2 + y2)+ xyr(x2 + y2)+ |
|||
+ 2ur 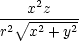 −
2u −
2u  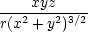 + ur
+ ur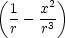 − − |
|||
− u 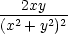 + u + u 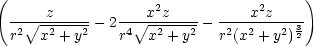 , , |
uyy
= urr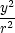 + u + u  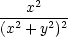 + u
+ u  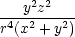 − 2ur
− 2ur 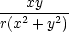 + + |
|||
+ 2ur 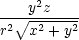 − 2u − 2u  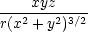 + ur + ur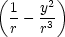 − − |
|||
− u 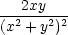 + u + u 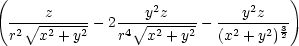 , , |
uzz
= urr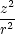 + u + u  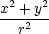 − 2ur − 2ur 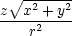 + + |
|||
+ ur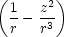 + u + u 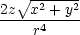 . . |

|
ii) Určete řešení Laplaceovy rovnice
v  3,
které je sféricky
symetrické, tj.
závisí pouze na vzdálenosti od
počátku.
3,
které je sféricky
symetrické, tj.
závisí pouze na vzdálenosti od
počátku.
Řešení. Nechť
funkce u závisí pouze na
proměnné r = 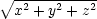 a nikoliv na
proměnných
a nikoliv na
proměnných  a
a  ,
tj. u = u(r) (tento
předpoklad je „rozumný“ vzhledem
k fyzikálnímu významu Laplaceovy
rovnice). Pak všechny
parciální derivace podle
,
tj. u = u(r) (tento
předpoklad je „rozumný“ vzhledem
k fyzikálnímu významu Laplaceovy
rovnice). Pak všechny
parciální derivace podle  ,
,  jsou
rovny nule a dostáváme rovnici
jsou
rovny nule a dostáváme rovnici
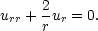
 v =
0 a po úpravě r2
vr + 2rv = 0, což je
ekvivalentní rovnici
v =
0 a po úpravě r2
vr + 2rv = 0, což je
ekvivalentní rovnici 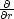 (r2v) = 0. Řešením této rovnice je např. v(r) = −
(r2v) = 0. Řešením této rovnice je např. v(r) = −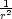 , a
tedy u =
, a
tedy u =  , tj.
, tj.
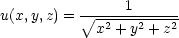
Nejprve připomeňme, co to je Taylorův polynom a
Taylorova věta2 pro funkci jedné proměnné.
Nechť f : 

 , x0,x
, x0,x

 a h
= x −
x0. Taylorův polynom (mnohočlen) stupně
n
a h
= x −
x0. Taylorův polynom (mnohočlen) stupně
n 
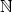 funkce
f se středem v bodě
x0 je polynom
funkce
f se středem v bodě
x0 je polynom
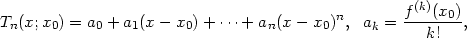
Taylorův polynom používáme k přibližnému výpočtu funkčních hodnot funkce f v okolí bodu x0. Taylorova věta udává velikost chyby, které se dopustíme, aproximujeme-li funkci Taylorovým polynomem.
Obdobně je tomu u funkce více proměnných.
Taylorův polynom funkce f
:  n
n

 je polynom více proměnných, který má
s funkcí f v daném
bodě x∗ =
[x1∗,…,xn∗]
je polynom více proměnných, který má
s funkcí f v daném
bodě x∗ =
[x1∗,…,xn∗]

 n
stejnou funkční hodnotu a stejnou hodnotu všech parciálních derivací až
do řádu n, kde
n je stupeň polynomu. Pro
funkce dvou proměnných dostáváme toto tvrzení.
n
stejnou funkční hodnotu a stejnou hodnotu všech parciálních derivací až
do řádu n, kde
n je stupeň polynomu. Pro
funkce dvou proměnných dostáváme toto tvrzení.
Věta 5.4. (Taylorova) Nechť funkce f
:  2
2

 má v bodě [x0,y0] a
nějakém jeho okolí spojité parciální derivace až do řádu
n +
1 včetně. Pak pro každý bod [x,y]
z tohoto okolí platí
má v bodě [x0,y0] a
nějakém jeho okolí spojité parciální derivace až do řádu
n +
1 včetně. Pak pro každý bod [x,y]
z tohoto okolí platí
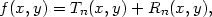 |
(5.10) |
kde
| Tn(x,y) | =
f(x0,y0) +
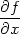 (x0,y0)h
+ (x0,y0)h
+ 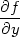 y(x0,y0)k+ y(x0,y0)k+ |
||
| + |  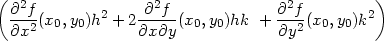 +
⋯+ +
⋯+ |
||
| + | 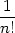 ∑ j=0n ∑ j=0n 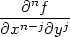 (x0,y0)hn−jkj, (x0,y0)hn−jkj, |
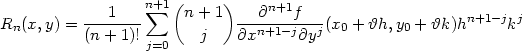
|

 (0,1).
(0,1).
Poznámka 5.4. Vzorec (5.10) se nazývá Taylorův vzorec, polynom Tn Taylorův polynom a Rn zbytek v Taylorově vzorci.
Taylorův vzorec lze zapsat pomocí diferenciálů takto:
| f(x,y) | =
f(x0,y0) +
df(x0,y0)(h,k) +
 d2f(x0,y0)(h,k) +
⋯+ d2f(x0,y0)(h,k) +
⋯+ |
||
+
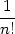 dnf(x0,y0)(h,k) + dnf(x0,y0)(h,k) +
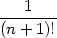 dn+1f(x0
+ dn+1f(x0
+  h,y0
+ h,y0
+  k)(h,k). k)(h,k). |
Důkaz Věty 5.4. Zaveďme pomocnou funkci jedné proměnné F(t) = f(x0 + th,y0 + tk). Platí F(1) = F(x0 + h,y0 + k) = F(x,y), F(0) = f(x0,y0). Pomocí Taylorova vzorce pro funkci jedné proměnné dostáváme
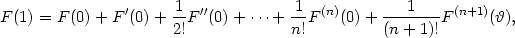

 (0,1). Pro
výpočet derivací funkce F
využijeme vztahů pro parciální derivace složených funkcí. Dostáváme
(0,1). Pro
výpočet derivací funkce F
využijeme vztahů pro parciální derivace složených funkcí. Dostáváme
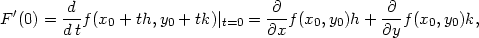
F  (0) = (0) = |
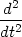 F(t) F(t) t=0 = t=0 = 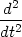 f(x0
+ th,y0
+ tk) f(x0
+ th,y0
+ tk) t=0 = t=0 = |
||
| = | fxx(x0,y0)h2 + 2fxy(x0,y0)hk + fyy(x0,y0)k2 |
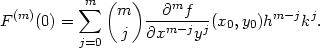
Příklad 5.4. i) Určete Taylorův polynom
2. stupně se středem v bodě [x0,y0] =
[1,1] pro funkci f(x,y) =
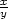 .
.
Řešení. Vypočteme nejprve všechny potřebné parciální derivace
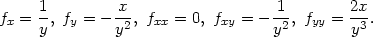
![T2(x, y) = f (1,1) + fx(1,1)(x − 1)+ fy(1,1)(y − 1)+ 1- 2 2 + 2 [fxx(1,1)(x− 1) + 2fxy(1,1)(x − 1)(y − 1)+ fyy(1,1)(y − 1) ] = = 1+ (x − 1)− (y − 1)− (x − 1)(y − 1)− (y − 1)2 = 2 = − y − xy + 2x+ 2y − 1.](diferencialni-pocet571x.png)
|
ii) Pomocí Taylorova polynomu 2. stupně vypočtěte přibližně:
a) 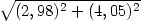 ; ; |
b) 1,042,02. |
Výsledek porovnejte s hodnotou získanou pomocí diferenciálu z Příkladu 4.2 ii).
Řešení. a) Přibližnou hodnotu vypočteme pomocí
Taylorova polynomu 2. stupně funkce z =
f(x,y) =
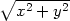 v bodě [x0,y0] =
[3,4] a diferencemi h =
−0,02,
k =
0,05. Parciální derivace
funkce z jsou
v bodě [x0,y0] =
[3,4] a diferencemi h =
−0,02,
k =
0,05. Parciální derivace
funkce z jsou
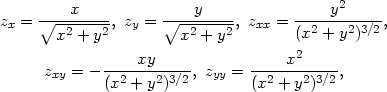
|
![T2(x, y) = f (3,4) + fx(3,4)(x − 3)+ fy(3,4)(y − 4)+ 1 + --[fxx(3,4)(x− 3)2 + 2fxy(3,4)(x − 3)(y − 4)+ fyy(3,4)(y − 4)2] = 2 = 5 + 1[3(x − 3)+4(y − 4)]+ -1-[16(x− 3)2− 24(x − 3)(y− 4)+9(y − 4)2]. 5 250](diferencialni-pocet575x.png)
|
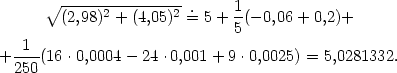
|
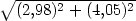 ≐5,028.
≐5,028.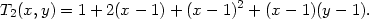
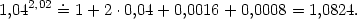
iii) Mnohočlen P(x,y) = x3 + 3y3 + xy2 + 2x2 + xy + x− 2y napište jako polynom v proměnných u = x − 1,v = y + 2.
Řešení. Nechť T3(x,y) Taylorův polynom 3. stupně funkce P se středem x0 = 1,y0 = −2. Pak ve zbytku R3(x,y) vystupují 4. derivace funkce P, které jsou však všechny nulové, neboť P je polynom 3. stupně. Tedy T3(x,y) = P(x,y) a stačí určit koeficienty v T3(x,y). Postupně dostáváme P(1 ,−2) = −20 Px = 3x2 + y2 + 4x + y + 1,Px(1,−2) = 10, Py = 9y2 + 2xy + x − 2,Py(1,−2) = 31, Pxx = 6x + 4, Pxx(1,−2) = 10, Pxy = 2y + 1,Pxy(1,−2) = −3, Pyy = 18y + 2x, Pyy(1,−2) = −34, Pxxx = 6,Pxxy = 0, Pxyy = 2,Pyyy = 18. Odtud
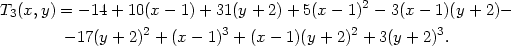
|
Zformulujme na závěr kapitoly ještě Taylorův vzorec pro obecný případ funkcí n proměnných. Důkaz tohoto tvrzení neuvádíme, neboť je v podstatě stejný jako pro dvě proměnné.
Věta 5.5. Nechť funkce f
:  n
n 
 má v bodě
x∗ = [x1∗,…,xn∗] a nějakém jeho
okolí spojité
parciální derivace
až do řádu m + 1. Pak pro
h =
[h1,…,hn] platí
má v bodě
x∗ = [x1∗,…,xn∗] a nějakém jeho
okolí spojité
parciální derivace
až do řádu m + 1. Pak pro
h =
[h1,…,hn] platí
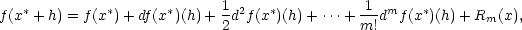
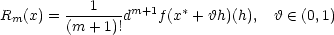
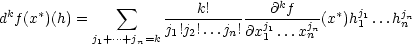
Cvičení 
5.1. Využitím uvedené substituce najděte
všechny funkce splňující danou rovnost:
a) yzx −
xzy =
0, u = x, v = 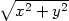
b) xzx +
yzy =
0, u = x, v = 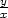
c) ux +
uy +
uz =
0,  =
x + y
− 2z,
=
x + y
− 2z,  =
x − 2y
+ z,
=
x − 2y
+ z, 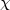 =
z
=
z
5.2. Diferenciální rovnice transformujte do
nových proměnných u,v.
V případech, kdy po transformaci vyjde jednoduchý výsledek, se
pokuste najít jejich řešení:
a) zxx −
yzyy − zy
= 0, u = x
− 2
zy
= 0, u = x
− 2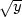 ,v
= x +
2
,v
= x +
2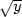
b) y2zxx
+ x2zyy
− 2xyzxy −
xzx −
yzy =
0,u = 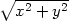 ,v =
xy
,v =
xy
c) x2zxx
− (x2
+ y2)zxy
+ y2zyy
= 0, u = x
+ y,v =
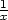 +
+ 
d) zxx −
2zxy
+ zyy
= 0, u = x
+ y,v =
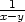
e) xyzxx −
(x2
+ y2)zxy
+ xyzyy +
yzx +
xzy =
0, u =  (x2
+ y2),
v = xy
(x2
+ y2),
v = xy
f) xzxx −
yzyy =
0, u = 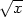 +
+
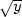 ,v =
,v = 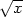 −
−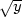
g) xzxx +
yzxy +
zx =
0,u = x
+ y,v =
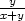
h) x2zxx
− 2xyzxy +
y2zyy
+ xzx
+ yzy
= 0, u =
xy, v =
y
i) x2zxx
− y2zyy
= 0, u =
xy, v =
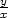
5.3. Ukažte, že daná transformace do nových
proměnných nemění tvar rovnice zxx
+ zyy
= 0, x =  (u,v),y
=
(u,v),y
= 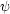 (u,v),
kde
(u,v),
kde  ,
,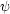 jsou funkce dvou proměnných splňující
identity
jsou funkce dvou proměnných splňující
identity  u =
u =
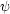 v,
v,  v
= −
v
= −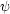 u.
u.
5.4. Určete Taylorův polynom 2. stupně se středem [x0,y0] následujících funkcí:
a) 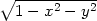 , [x0,y0] =
[ , [x0,y0] =
[ , , ] ] |
e) arcsin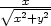 , [x0,y0] =
[0,1] , [x0,y0] =
[0,1] |
b) arctg 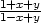 , [x0,y0] =
[0,0] , [x0,y0] =
[0,0] |
f) ln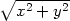 , [x0,y0] =
[1,1] , [x0,y0] =
[1,1] |
c) 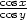 , [x0,y0] =
[0,0] , [x0,y0] =
[0,0] |
g) x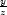 , [x0,y0,z0] =
[1,1,1] , [x0,y0,z0] =
[1,1,1] |
d) arctg
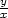 , [x0,y0] =
[1,1] , [x0,y0] =
[1,1] |
h) sinxsiny, [x0,y0] = [0,0] |
5.5. Pomocí Taylorova polynomu 2. stupně
vypočtěte přibližně funkční hodnoty:
a) arctg 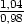 b) sin29
b) sin29 tg 46
tg 46
1Pierre Simon Laplace (1749–1827), francouzský matematik, fyzik a astronom
2Brook Taylor (1685–1731), anglický matematik
[Další] [Předchozí] [Předchozí – na konec] [Na začátek] [Výše]