[Další] [Předchozí] [Předchozí – na konec] [Na konec] [Výše]

Využití počítače ve výuce matematické analýzy

Rychlý rozvoj výpočetní techniky v současnosti ovlivňuje téměř všechny oblasti lidského života. Stranou nezůstává ani proces výuky na vysokých školách. V našich podmínkách bylo zatím použití počítače ve výuce spíš nahodilé a bylo ponecháváno na iniciativě vyučujících. Až v poslední době se tímto způsobem výuky začíná zabývat větší počet vyučujích, kteří si své zkušenosti sdělují na konferencích pořádáných Českým sdružením uživatelů Maplu a na celostátních seminářích kateder matematiky fakult připravujících učitele matematiky (např. Počítačem podporovaná výuka matematiky a příprava didaktického experimentu, Rybník u Poběžovic, 8.–11. září 1998).

Otázky tohoto způsobu výuky však nejsou zatím souhrnně zpracovány a zodpovězeny. Tato kapitola je proto věnována problematice využití výpočetní techniky ve výuce matematické analýzy. Jejím cílem je ukázat možnosti tohoto způsobu výuky a najít odpověď na otázky kde, proč a jak používat počítač při výuce matematické analýzy a zároveň upozornit i na úskalí používání počítačových systémů ve výuce.

Využití počítače ve výuce matematické analýzy může být na základě našich zkušeností rozděleno následujícím způsobem:

Počítačová grafika – pod tímto termínem budeme v dalším rozumět jakýkoliv grafický výstup pořízený počítačem (obrazovka, tiskárna, ploter…). Grafika může být statická (graf funkce) nebo dynamická (animace v CAS systémech).
Počítačové řešení úloh – pod počítačovým řešením úloh rozumíme využití počítače při řešení zadaného matematického problému.

Úlohy, při kterých získáváme řešení pouze použitím standardního příkazu systému, nebudeme uvažovat. V takovém případě je pro nás počítač jakousi „černou skříňkou“, která nám dává výsledek bez našeho přispění a bez pochopení, co se děje „uvnitř“. Naše pozornost bude soustředěna na netriviální a smysluplné použití počítače při řešení matematických problémů, tj. tam, kde počítač pomáhá při:

Vedle těchto dvou základních způsobů využití počítače ve výuce matematické analýzy někdy používáme i programy k testování znalostí. Ty slouží k mechanickému procvičování a prověřování získaných vědomostí a dovedností. Protože program Maple V není určen k tvorbě takových testů, uvádíme pouze v kapitole 16 odkazy na testovací programy na Internetu.

Pokusme se nyní nalézt odpovědi na otázky položené v předcházejícím odstavci.

Kde

Kde, přesněji ve které fázi a formě výuky a vzdělávání v matematické analýze lze efektivně využívat výpočetní techniku? Ze získaných zkušeností plyne, že výpočetní techniku lze používat při:

Při přednáškách využíváme nejčastěji počítačovou grafiku. Méně časté je použití počítačového řešení úloh, ale i to nachází při přednáškách uplatnění, a to zejména při usnadnění zdlouhavých výpočtů a při úpravách výrazů. Testovací programy při přednáškách nevyužíváme.

Při cvičeních hraje klíčovou roli počítačové řešení úloh, které je doplněno počítačovou grafikou a testovacími programy (myšlena jsou speciální cvičení v počítačové laboratoři).

Totéž platí i pro samostatnou přípravu, pouze roste úloha testovacích programů.

 

Proč

Proč výpočetní techniku, přesněji výše uvedené způsoby, ve výuce matematické analýzy využívat?
Geometrická představivost hraje v matematické analýze významnou úlohu (studenti někdy nemají s daným matematickým pojmem spojenu konkrétní geometrickou představu). K jejímu vytváření významnou měrou přispívá i počítačová grafika. Ta umožňuje vytvářet tuto geometrickou představu i v případech, které jsou bez použití počítače jen těžko realizovatelné (viz např. obr.  11.6). Při řešení příkladů si pak student může vytvořit geometrickou představu o tom, co má počítat, a může získané výsledky s počítačovou grafikou konfrontovat (viz např. příklad 14.4 ).

Zjednodušení rutinních výpočtů umožní studentům věnovat více času výběru metody řešení a interpretaci výsledků. V důsledku toho můžeme obohatit různorodost typů, zvýšit počet a prohloubit náročnost problémů, které studenti samostatně řeší. Ilustrací takového přístupu je například určování limity funkce dvou proměnných (kapitola 11.2 ). Nezanedbatelný je i příspěvek počítačového řešení úloh k opakování a prohloubení učiva. Ilustrujme tento přístup na hledání stacionárních bodů funkce dvou proměnných (příklad 14.1). Student musí nejdříve sám sestavit soustavu rovnic pro nalezení stacionárních bodů. Počítače pak využije k výpočtu odpovídajících parciálních derivací a k výpočtu soustavy rovnic (při řešení postupuje stejně jako při řešení pomocí „tužky a papíru“, pouze vlastní zápis provádí formou příkazů zvoleného počítačového systému). Dalším stupněm je pak automatizace tohoto postupu pomocí programovacího jazyka zvoleného systému. Počítačové řešení úloh přispívá i k objasnění teoretických pojmů a prohloubení jejich pochopení (např. znázornění geometrického významu směrových derivací, kapitola 12.2 ). Ve všech uvedených případech studentům použití počítače umožňuje soustředit se na podstatu problému více než na mechanické zvládnutí výpočtu.

Použití počítače ve výuce má však i svá úskalí. Ne vždy totiž počítačovým programem získáme výsledek, který odpovídá skutečnosti. Při výuce studentů u počítače je proto třeba klást důraz na interpretaci a kontrolu získaných výsledků. Studenti mají často tendenci používat počítačový program mechanicky, bez uvažování. Uveďme si jeden ilustrační příklad:

Příklad.  Pomocí počítače nakreslete graf funkce f(x) = ex + ln∣(4 −x)∣ pro x ∈〈0,5〉.
K řešení byl použit systém Maple.
> f:=x->E**x+ln(abs(4-x));

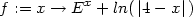
x f := x → E + ln( ∣4 − x∣)


> plot(f(x),x=0..5, labels=[x,y]);

Řada studentů se zde soustředí především na syntaxi příkazu a je se získaným výsledkem spokojena (obr. 1). Podrobnější analýzou zadané funkce ale zjistíme, že tato funkce f je v bodě 4 nespojitá a lim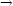x→4f(x) = −∞. Grafický výstup proto poté upravíme přidáním parametru discont=true a zvýšením počtu referenčních bodů (tj. bodů, které Maple používá k aproximaci zadané funkce). Pro větší názornost volíme x z intervalu 〈3.9,4.1〉 (obr. 2).
> plot(f(x), x=3.9..4.1, y=47..58, numpoints=500,
> discont=true, labels=[x,y]);

PIC

obr. 1:
PIC
obr. 2:

V dalších částech práce průběžně upozorňujeme na nebezpečí bezmyšlenkovitého použití počítače. Budou uvedeny příklady, kdy počítač dává nesprávné nebo neúplné výsledky (obr. 10.5 , příklad 14.4 …). Ty jsou na druhou stranu důležité z hlediska motivace. Ukazují, že počítač není „všemocný“ – teprve porozumění probírané látce dělá z počítače skutečně „mocného“ pomocníka.

Jak

Jak, přesněji s jakým technickým vybavením a při jaké organizaci výuky (časové i obsahové) počítačem podporovanou výuku realizovat?
Zabývejme se nejdříve podrobněji technickou realizací uvedených způsobů použití počítače ve výuce matematické analýzy. Pro využití počítače při přednáškách je nejvýhodnější v posluchárně trvale instalovat počítač s projektorem, případně LCD panelem a promítacím plátnem. Při tomto uspořádání může projekční plátno sloužit jako „inteligentní tabule“, kdy např. můžeme změnou parametrů zadání již vyřešeného příkladu okamžitě vyřešit příklad modifikovaný. Výhodou tohoto uspořádání je tedy možnost dynamické změny parametrů (např. oproti grafickým výstupům připraveným na tiskárně) a přímé interakce vyučujícího s počítačovým programem. Příklady počítačového řešení úloh by bez tohoto uspořádání bylo jen obtížně možno na přednáškách realizovat. Pokusy s konáním přednášek přímo v počítačové učebně končily většinou nezdarem. Studenti v tomto případě věnovali větší pozornost interakci s počítačem než výkladu vyučujícího. Další nevýhodou pak bylo různé tempo postupu. Studenti s menší znalostí práce s počítačem nebyli schopni po určité době výklad sledovat.

Dále se ukázalo, že naproti tomu cvičení je optimální provádět v počítačové učebně, a to tak, aby každý student pracoval u svého počítače či terminálu. Výhodou je možnost individuálního postupu u každého studenta. Nezbytná je také podmínka volného přístupu studentů do počítačové učebny, protože řada úkolů je určena k samostatnému řešení během týdne.

Kromě nezbytného hardwaru je zapotřebí i vhodný software. Pro matematickou analýzu je nejvýhodnější zajištění některého z CAS systémů, výuku je však možno realizovat i pomocí specializovanějších public domain programů, které jsou volně přístupné na počítačové síti Internet. K výuce některých partií je možno využívat také interaktivní programy, přístupné na Internetu. O těchto možnostech bude podrobněji pojednáno v kapitole 16 .

Druhá otázka – začlenění počítačem podporované výuky do osnov – závisí zejména na typu (zaměření) školy. Ideální by bylo přidat k současným „klasickým“ cvičením ještě další hodiny počítačové výuky.

V USA v rámci projektu CALC (Calculus As a Laboratory Course) byla klasická cvičení zrušena úplně, výpočetní operace a metody jsou procvičovány v rámci počítačové výuky. Dosavadní výsledky a hodnocení projektu ukazují, že studenti zahrnutí do projektu dosahují u zkoušek lepších výsledků a hlubšího pochopení látky než studenti v tradičních třídách, v těchto třídách je ale na vyšší úrovni početní zručnost. Informace o projektu je možno nalézt na adrese http://www.math.duke.edu/education/proj_calc/.

Zavedení výuky podobné projektu CALC však v našich podmínkách naráží na téměř nulovou možnost zvýšení počtu hodin věnovaných výuce matematické analýzy. Stávající sylabus je dimenzován tak, že zavedení počítačové výuky by bylo na úkor současného obsahu učiva. Snížení počtu hodin klasických cvičení na úkor počítačových laboratoří by mohlo mít za následek snížení početních schopností studentů, což je zejména u studentů učitelského studia jevem nežádoucím. Těžiště využití počítače je zde tedy především při přednáškách a jako doplnění klasických cvičení (zejména příklady ilustrační grafiky). Ukázkami ve výuce a při cvičeních by studenti měli být motivováni k samostatné práci a k experimentování v počítačové laboratoři. (Předpokladem je opět volný přístup do počítačové laboratoře vybavené vhodným softwarem.)

Snazší je zavedení výuky v počítačových laboratořích na školách, kde je matematika aplikovanou vědou, tj. zejména na vysokých školách technického směru. Zde můžeme rozdělit cvičení na část klasickou a počítačovou (např. střídavě po 14 dnech jako na strojní fakultě VUT v Brně). U těchto oborů je výhodné, aby po analýze problému vlastní výpočet provedl počítač. (Není zde kladen takový důraz na početní zručnost studentů.)

 

Technické poznámky

V počátečních kapitolách počítačového zpracování tématu je v textu řešení příkladů zápis uváděn ve dvojí podobě. Nejdříve je uveden obvyklý matematický zápis (sazba je provedena systémem LATEX) a následně zápis výpočtu v Maplu. Poté co si čtenář postupně zvykne na zápis v Maplu, je matematický zápis vynecháván a uváděny jsou již pouze příkazy Maplu. Mapleovské vstupy jsou v textu označovány > a změnou typu písma na strojopisné. Vstup (zadání příkazu) je v Maplu ukončován pomocí znaků ; nebo:. Pokud je vstup zakončen znakem ;, následují ihned řádky s výstupem, při ukončení pomocí : se řádky s výstupem nevypisují na obrazovku, a nejsou tedy uvedeny ani v textu. Vstupy a výstupy byly získány exportem (automatickým převedením) Mapleovských zápisníků do systému TEX (v textu je vždy uvedena úplná posloupnost příkazů). Všechny procedury naprogramované pro účely této práce jsou uloženy v knihovně mvcalp. Při programování procedur byl větší důraz kladen na jednoduchost a matematickou správnost než na programátorskou efektivnost a úplnost tak, aby procedury nebyly zbytečně složité a aby je byli schopni vytvářet i studenti bez hlubší znalosti programovacích jazyků. Knihovna mvcalp a všechny Mapleovské zápisníky s ilustračními příklady jsou taktéž uloženy na CD-ROM. Všechny obrázky jsou uloženy v PostScriptu1 a jsou přístupné také prostřednictvím Internetu na adrese http://www.math.muni.cz/~plch/difer/difer.html.

Maple V R3 byl zvolen pro snadné ovládání a dostupnost. Během tvorby práce došlo k dalšímu vývoji programu, proto se v práci vyskytují i odkazy na verzi Maple V R4 (verze Maple V R5 byla k dispozici teprve až v době závěrečného zpracování, proto na ni v textu neodkazujeme). Maple byl provozován na počítači s operačním systémem Linux. Přechodem k jinému operačnímu systému (Windows 9x, Me, 2000, XP) může dojít k prodloužení doby potřebné k výpočtu (zejména u generování grafiky).

1Jeden z nejpoužívanějších jazyků pro popis stránky (PDL), vyvinutý společností Adobe Systems.

[Další] [Předchozí] [Předchozí – na konec] [Na začátek] [Výše]