
[Další] [Předchozí] [Předchozí – na konec] [Na konec] [Výše]

Obrázky ke cvičením Kapitoly 1 jsou uvedeny na závěr.
2.1 a) Ke
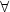 A
A

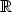

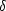 > 0
takové, že pro
> 0
takové, že pro 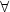 [x,y],
pro něž 0 <
[x,y],
pro něž 0 <  x +
1
x +
1 <
< 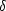 , 0
<
, 0
<  y
− 2
y
− 2 <
< 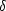 platí f(x,y)
> A. b) Ke
platí f(x,y)
> A. b) Ke 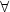 A
A

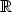

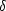 > 0, B
> 0, B 
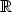 taková, že
pro
taková, že
pro 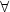 x >
B,
x >
B,  y
− 1
y
− 1 <
< 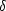 je f(x,y)
< A. 2.2 a)
je f(x,y)
< A. 2.2 a) 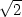 b) 2 c) ln2 d)
0 e) 0. 2.3 a) neexistuje b) neexistuje
c) 0 d) 1 e) 0 f) 2 g) 0 h) 2.
2.4 a) 0 b) e c) neexistuje d) 0 e) 0
f) 1. 2.6 a) f je spojitá v
b) 2 c) ln2 d)
0 e) 0. 2.3 a) neexistuje b) neexistuje
c) 0 d) 1 e) 0 f) 2 g) 0 h) 2.
2.4 a) 0 b) e c) neexistuje d) 0 e) 0
f) 1. 2.6 a) f je spojitá v 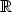 2
2 [0,0]
b) {[x,y] :
x = −y}
c) {[x,y] :
x = −y}
d) {[x,y] :
x = 0 nebo y =
0} e) {[x,y] :
x = kp, y
= kp, k
[0,0]
b) {[x,y] :
x = −y}
c) {[x,y] :
x = −y}
d) {[x,y] :
x = 0 nebo y =
0} e) {[x,y] :
x = kp, y
= kp, k 
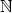 } f) {[x,y] :
x2 +
y2 =
1}. 2.7 a) {[x,y] :
x = −y nebo
x =
0} b) {[x,y] :
y =
} f) {[x,y] :
x2 +
y2 =
1}. 2.7 a) {[x,y] :
x = −y nebo
x =
0} b) {[x,y] :
y = 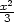 } c) {[x,y] :
x = 0, y
= 0} d) {[x,y] :
y = 0} e)
{[x,y,z] :
x = 0 nebo y = 0
nebo z = 0} f)
{[x,y,z] =
[a,b,c]}.
2.8 a) je spojitá b) není
spojitá.
} c) {[x,y] :
x = 0, y
= 0} d) {[x,y] :
y = 0} e)
{[x,y,z] :
x = 0 nebo y = 0
nebo z = 0} f)
{[x,y,z] =
[a,b,c]}.
2.8 a) je spojitá b) není
spojitá.
3.1 a)
zx =
3x2 +
4xy + 3y2
+ 4, zy
= 2x2
+ 6xy −
5 b) zx
= 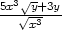 , zy
=
, zy
= 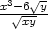 c) zx
= sin(x
+ 2y) +
xcos(x
+ 2y),
zy =
2xcos(x
+ 2y) d)
zx =
c) zx
= sin(x
+ 2y) +
xcos(x
+ 2y),
zy =
2xcos(x
+ 2y) d)
zx =
 cos
cos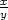 cos
cos +
+ 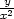 sin
sin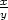 sin
sin , zy =
−
, zy =
−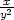 cos
cos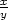 cos
cos −
− sin
sin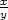 sin
sin e) ux
=
e) ux
= 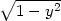 −
−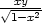 +
+ 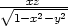 , uy
= −
, uy
= −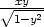 +
+ 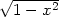 +
+ 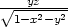 ,
uz =
−
,
uz =
−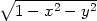 f) zx
= −
f) zx
= − e−
e−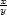 , zy
=
, zy
= 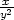 e−
e−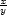 g) zx
=
g) zx
= 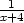 , zy =
−
, zy =
−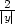 h) zx
=
h) zx
= 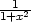 , zy =
−
, zy =
−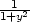 i) zx
= −
i) zx
= −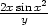 , zy
= −
, zy
= −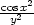 j) zx
=
j) zx
= 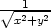 , zy
=
, zy
= 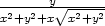 k) ux
= 2xex2(1−y−z) , uy
= uz
= −ex2(1−y−z) l) zx
=
k) ux
= 2xex2(1−y−z) , uy
= uz
= −ex2(1−y−z) l) zx
= 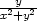 , zy =
−
, zy =
−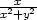 m) zx
=
m) zx
= 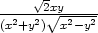 ,
zy =
−
,
zy =
− n)
n) 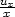 =
=
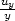 =
= 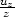 =
= 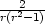 , kde r =
, kde r = 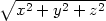 . 3.2 a) zx
= yxxy(1 +
lny),
zy =
xxy+1 lnx
b) zx =
−
. 3.2 a) zx
= yxxy(1 +
lny),
zy =
xxy+1 lnx
b) zx =
−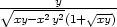 ,
zy =
−
,
zy =
−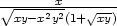 , c) zx
= −
, c) zx
= − (
(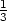 )
)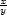 ln3, zy
=
ln3, zy
= 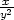 (
(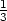 )
)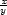 ln3 d) zx
= y[ln(x
+ y) +
ln3 d) zx
= y[ln(x
+ y) +
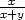 ], zy
= x[ln(x
+ y) +
], zy
= x[ln(x
+ y) +
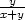 ]
e) zx =
2(2x + y)(2x+y)[ln(2x
+ y) + 1],
zy =
(2x + y)(2x+y)[ln(2x
+ y) + 1]
f) zx =
−
]
e) zx =
2(2x + y)(2x+y)[ln(2x
+ y) + 1],
zy =
(2x + y)(2x+y)[ln(2x
+ y) + 1]
f) zx =
−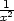
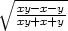 , zy
= −
, zy
= −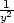
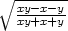 g) zx
= yesin
pxy(1 +
pxy cos
pxy),
zy =
xesin
pxy(1 +
pxy cos
pxy)
h) ux =
g) zx
= yesin
pxy(1 +
pxy cos
pxy),
zy =
xesin
pxy(1 +
pxy cos
pxy)
h) ux =
 x(
x(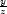 −1), uy
=
−1), uy
=  x
x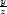 lnx, uz
= −
lnx, uz
= −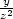 x
x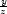 lnx i) zx
=
lnx i) zx
= 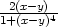 , zy
= −
, zy
= −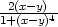 j)
j) 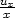 =
=
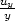 =
= 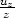 = 2cos(x2
+ y2
+ z2)
k) ux =
yzxyz−1, uy
= xyz zyz−1 lnx,
uz =
xyz yz
lnxlny.
3.3 a) zx
= 2
= 2cos(x2
+ y2
+ z2)
k) ux =
yzxyz−1, uy
= xyz zyz−1 lnx,
uz =
xyz yz
lnxlny.
3.3 a) zx
= 2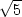 , zy = 10 +
, zy = 10 +
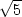 b) zx
= 0, zy
=
b) zx
= 0, zy
=  c) zx
= 1, zy
= −1.
3.4 a)
c) zx
= 1, zy
= −1.
3.4 a) 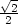 b)
b) 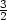 . 3.6 a) zxx
= 12x2
− 8y2,
zxy =
−16xy,
zyy =
12y2 −
8x2
b) zxx = 0,
zxy = 1
−
. 3.6 a) zxx
= 12x2
− 8y2,
zxy =
−16xy,
zyy =
12y2 −
8x2
b) zxx = 0,
zxy = 1
−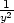 , zyy =
, zyy =
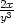 c) zxx
= 0, zxy
= −
c) zxx
= 0, zxy
= −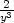 , zyy
=
, zyy
= 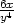 d) zxx
= −
d) zxx
= −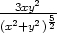 ,
zxy =
,
zxy =
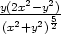 , zyy
= −
, zyy
= −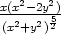 e) zxx =
2cos(x
+ y)
− xsin(x
+ y),
zxy =
cos(x
+ y)
−xsin(x
+ y),
zyy =
−xsin(x
+ y)
f) zxx =
−
e) zxx =
2cos(x
+ y)
− xsin(x
+ y),
zxy =
cos(x
+ y)
−xsin(x
+ y),
zyy =
−xsin(x
+ y)
f) zxx =
−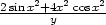 , zxy
=
, zxy
= 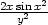 , zyy
=
, zyy
= 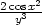 g) zxx
= x(x+y)[(lnx
+
g) zxx
= x(x+y)[(lnx
+ 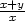 )2 +
)2 +
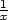 −
−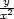 ], zxy
= x(x+y)[ln2x
+
], zxy
= x(x+y)[ln2x
+ 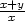 lnx +
lnx +
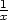 ], zyy
= x(x+y) ln2x
h) zxx =
], zyy
= x(x+y) ln2x
h) zxx =
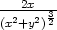 , zxy
=
, zxy
= 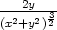 , zyy
= −
, zyy
= −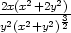 i) zxx =
−
i) zxx =
−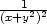 , zxy =
−
, zxy =
−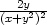 , zyy =
, zyy =
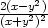 j) zxx
=
j) zxx
= 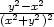 , zxy
= −
, zxy
= −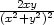 , zyy
=
, zyy
= 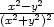 k) zxx
= −
k) zxx
= −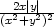 , zxy
=
, zxy
= 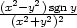 , zyy
=
, zyy
= 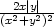 l) zxx
= 2y(1 +
x2)y−2(−x2
+ 2x2y
+ 1), zxy
= 2x(1 +
x2)y−1[1 +
y ln(1 +
x2)],
zyy = (1 +
x2)y
ln2(1 +
x2).
l) zxx
= 2y(1 +
x2)y−2(−x2
+ 2x2y
+ 1), zxy
= 2x(1 +
x2)y−1[1 +
y ln(1 +
x2)],
zyy = (1 +
x2)y
ln2(1 +
x2).
4.1
a) 2dx b) 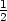 dx −
dx −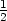 dy c)
dy c) 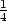 dx −
dx −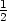 dy d) dx +
2ln2dy
− 2ln2dz
e)
dy d) dx +
2ln2dy
− 2ln2dz
e) 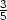 dx
+
dx
+ 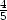 dy
f) df =
dy
f) df = 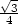 dx −
dx − dy g) df =
−2dx
+ dz h) du =
dy g) df =
−2dx
+ dz h) du =
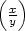

![[ ] dx-− dy − dz2 ln x x y z y](diferencialni-pocet1833x.png) 4.2
a)
4.2
a)  +
0,035 b)
+
0,035 b) 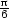 −
−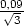 c) 2,
95 d) −0,06
e) 1 f) 1,13
g) dV ≐
c) 2,
95 d) −0,06
e) 1 f) 1,13
g) dV ≐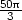 cm3 h) dh≐ 1
cm. 4.3 a) není
diferencovatelná, např. pro u
= (1,1)
neexistuje směrová derivace fu(0,0)
b) není diferencovatelná, neboť f(1,1)(0,0)
neexistuje c) ano df(0,0) = 0
4.4 a) x +
y + z
=
cm3 h) dh≐ 1
cm. 4.3 a) není
diferencovatelná, např. pro u
= (1,1)
neexistuje směrová derivace fu(0,0)
b) není diferencovatelná, neboť f(1,1)(0,0)
neexistuje c) ano df(0,0) = 0
4.4 a) x +
y + z
= 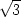 b) 3x +
5y − z
= 4 c) z0
= −
b) 3x +
5y − z
= 4 c) z0
= − , x + y
− 2z
=
, x + y
− 2z
= 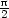 d) z0
= 1, z =
1. 4.5 a) [2,1],
[−2,−1]
b)
d) z0
= 1, z =
1. 4.5 a) [2,1],
[−2,−1]
b) ![[ −a −b ] √1+a2+b2,√1+a2+b2](diferencialni-pocet1841x.png) c) [−1∕2,1∕2]
d) [1,1]
e) [
c) [−1∕2,1∕2]
d) [1,1]
e) [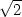 ,
,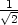 ,−
,−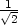 ], [−
], [−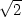 ,−
,−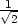 ,
,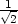 ] f) tečna existuje ⇔ a12
+ ⋯ +
an2
= 1; pak [x1,…,xn] =
[−a1,…,−an].
4.6 a) f(1,2)(1,1) = 3
b) f(1,0,1)(0,1,0) = 0.
4.7 a) d2z
=
] f) tečna existuje ⇔ a12
+ ⋯ +
an2
= 1; pak [x1,…,xn] =
[−a1,…,−an].
4.6 a) f(1,2)(1,1) = 3
b) f(1,0,1)(0,1,0) = 0.
4.7 a) d2z
= 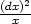 +
+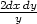 −
−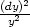 b) d2z
= 6(x−y)(dx)2
+12(y−x)dxdy
+6(x−y)(dy)2
c) dnz
= ex+y ∑
j=0n
b) d2z
= 6(x−y)(dx)2
+12(y−x)dxdy
+6(x−y)(dy)2
c) dnz
= ex+y ∑
j=0n [n2
+2j2
−2nj
−n+x2
+y2
+2xj +2(n−j)y](dx)j(dy)n−j d) dnz
=
[n2
+2j2
−2nj
−n+x2
+y2
+2xj +2(n−j)y](dx)j(dy)n−j d) dnz
= 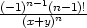 (dx+dy)n
e) dnz
=
(dx+dy)n
e) dnz
= 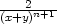 ∑ j=0n(−1)j
∑ j=0n(−1)j
![[(n − j)x + jy]](diferencialni-pocet1855x.png) (dx)j(dy)n−j f) dnu
= n!ex+y+z ∑
i+j+k=n
(dx)j(dy)n−j f) dnu
= n!ex+y+z ∑
i+j+k=n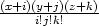 (dx)i(dy)j(dz)k.
4.8 a)
(dx)i(dy)j(dz)k.
4.8 a) 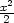 + xlny
− cosy
+ C, b)
+ xlny
− cosy
+ C, b) 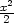 sin2y
+ C c)
sin2y
+ C c) 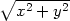 + C d) xy2
− x +
+ C d) xy2
− x +
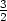 y2
+ C. 4.9
a) x3 +
y3 +
z3 −
3xyz +
2x + y
lny +
z b) arctg xyz.
y2
+ C. 4.9
a) x3 +
y3 +
z3 −
3xyz +
2x + y
lny +
z b) arctg xyz.
5.1 a)
z(x,y) =
f(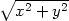 ) b) z(x,y) =
f
) b) z(x,y) =
f c) u(x,y,z) =
f(x+y−2z,x−2y+z).
5.2 a) zuv
= 0, z(x,y) =
f(x
− 2
c) u(x,y,z) =
f(x+y−2z,x−2y+z).
5.2 a) zuv
= 0, z(x,y) =
f(x
− 2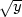 ) +
g(x
+ 2
) +
g(x
+ 2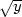 ) b) zvv0,
z(x,y) =
f(
) b) zvv0,
z(x,y) =
f(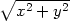 )+xyg(
)+xyg(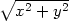 ) c) u(4−uv)zuv−2zv
= 0 d) zvv+2v3zv
= 0 e) (u2
−v2)zuv
−vzu
= 0 f) (u2
−v2)zuv
+vzu
−uzv
= 0 g) uzuu
−xzuv
+zu
= 0. h) vzvv+zv
= 0, z(x,y) =
f(xy)lny
+g(xy).
i) zuv =
) c) u(4−uv)zuv−2zv
= 0 d) zvv+2v3zv
= 0 e) (u2
−v2)zuv
−vzu
= 0 f) (u2
−v2)zuv
+vzu
−uzv
= 0 g) uzuu
−xzuv
+zu
= 0. h) vzvv+zv
= 0, z(x,y) =
f(xy)lny
+g(xy).
i) zuv =
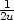 zv,
z(x,y) =
zv,
z(x,y) =
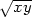 f(
f(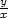 )g(xy).
5.4 a) T2(x,y) =
)g(xy).
5.4 a) T2(x,y) =
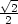 +
+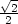 [(x−
[(x− )+(y−
)+(y− )]−
)]−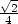 [(x−
[(x− )2
+2(x−
)2
+2(x− )(y−
)(y− )+(y−
)+(y− )2]
b) T2(x,y) =
)2]
b) T2(x,y) =
 + x −
+ x −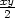 c) T2(x,y) = 1
−
c) T2(x,y) = 1
−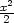 +
+ 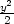 d) T2(x,y) =
d) T2(x,y) =
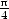 −
−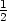 (x −
1) +
(x −
1) + 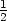 (y −
1) +
(y −
1) + 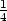 (x −
1)2 −
(x −
1)2 −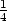 (y
− 1)2
e) T2(x,y) =
x−x(y
−1) f) T2(x,y) =
(y
− 1)2
e) T2(x,y) =
x−x(y
−1) f) T2(x,y) =
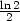 +
+ [(x−1)+(y
−1)]−
[(x−1)+(y
−1)]− (x−1)(y
−1) g) T2(x,y,z) = 1 +
(x− 1) +
(x− 1)(y
− 1) −
(x−
1)(z −
1). 5.5 a)
(x−1)(y
−1) g) T2(x,y,z) = 1 +
(x− 1) +
(x− 1)(y
− 1) −
(x−
1)(z −
1). 5.5 a) 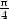 + 0,0297 b)
+ 0,0297 b)
 +
+ 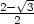
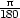 +
+ 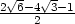
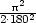 .
.
6.1
a) zmin =
−1 v bodě [1,0]
b) zmax =
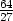 v [
v [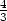 ,
,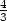 ], ve stacionárních bodech [0,0],[0,4],[4,0]
extrém nenastává c) zmax
= 16 v [2,−2]
d) zmin = 30
v [5,2]
e) zmin = 3 +
ln3 v [1,1],
f) V jediném stacionárním bodě [1,1]
extrém nenastává g) zmin
= −
], ve stacionárních bodech [0,0],[0,4],[4,0]
extrém nenastává c) zmax
= 16 v [2,−2]
d) zmin = 30
v [5,2]
e) zmin = 3 +
ln3 v [1,1],
f) V jediném stacionárním bodě [1,1]
extrém nenastává g) zmin
= −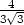 v [−
v [−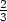 ,−
,−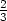 ] h) umin
= −6913
v [24,−144,−1]
i) umin = 4
v [
] h) umin
= −6913
v [24,−144,−1]
i) umin = 4
v [ ,1,1]
j) zmin =
3
,1,1]
j) zmin =
3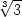 a2
v [
a2
v [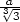 ,
,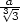 ]
k) umax =
]
k) umax =
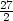 , v [3,
, v [3,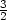 ,1]
l) umax =
,1]
l) umax =
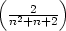
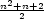 v x1
= ⋯ =
xn =
v x1
= ⋯ =
xn =
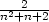 m) umin
= (n +
1)2
m) umin
= (n +
1)2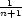 v x1
= 2
v x1
= 2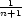 , x2
= 2
, x2
= 2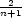 ,…xn
= 2
,…xn
= 2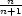 . 6.3
a) fmin =
−2 v [−1,−1],
fmax = 2
v [1,1]
b) fmin =
. 6.3
a) fmin =
−2 v [−1,−1],
fmax = 2
v [1,1]
b) fmin =
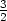 v [
v [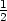 ,
,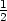 ], fmax
= 3 v [0,0],
c) fmin = 2
−
], fmax
= 3 v [0,0],
c) fmin = 2
−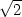 v [1 −
v [1 −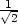 ,1
−
,1
−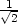 ], fmax
= 2 +
], fmax
= 2 + 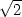 v [1 +
v [1 + 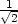 ,1 +
,1 + 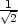 ] d) fmin
= −
] d) fmin
= −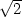 v [−
v [−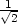 ,−
,−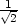 ,0],
fmax =
,0],
fmax =
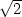 + 1
v [
+ 1
v [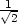 ,
,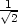 ,1] e) fmin
= 0 v [0,0,0],
fmax = 1
v bodech [x,y,0],
kde x2 +
y2 = 1.
6.4 a) fmax
= 7 v [0,−1],
fmin =
−4 v [1,1]
b) fmax = 22
v [2,2],
fmin =
−2 v [−2,2]
c) fmax = 6
v [3,0],
fmin =
−1 v [1,1]
d) fmax =
−
,1] e) fmin
= 0 v [0,0,0],
fmax = 1
v bodech [x,y,0],
kde x2 +
y2 = 1.
6.4 a) fmax
= 7 v [0,−1],
fmin =
−4 v [1,1]
b) fmax = 22
v [2,2],
fmin =
−2 v [−2,2]
c) fmax = 6
v [3,0],
fmin =
−1 v [1,1]
d) fmax =
−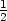 v [−
v [−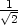 ,
,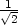 ], fmin
= −2
v [0,0].
e) fmin = 0
v [0,0],
fmax = 12 v
bodech [0,
], fmin
= −2
v [0,0].
e) fmin = 0
v [0,0],
fmax = 12 v
bodech [0, 3]. f) fmin
= 3 − 2
3]. f) fmin
= 3 − 2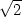 v bodě [
v bodě [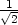 ,−
,−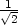 ], fmax
= 3 + 2
], fmax
= 3 + 2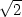 v bodě
[−
v bodě
[−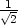 ,
,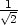 ]. 6.5
a) fmax =
]. 6.5
a) fmax =
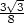 v [
v [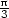 ,
,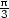 ], fmin
= −
], fmin
= −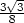 v [
v [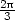 ,
,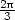 ] b) fmax
= 1 v [
] b) fmax
= 1 v [ 1,0] a
[0,
1,0] a
[0, 1], fmin
= 0 v [0,0]
c) fmax = 3 +
1], fmin
= 0 v [0,0]
c) fmax = 3 +
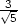 v [
v [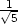 ,
,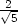 ,1],
fmin =
−
,1],
fmin =
−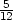 v [−
v [− ,−
,− ,
,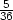 ] d) Čísla a,x1,x2,…,xn,b tvoří
geometrickou posloupnost s kvocientem q =
] d) Čísla a,x1,x2,…,xn,b tvoří
geometrickou posloupnost s kvocientem q =
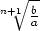 .
.
7.1
a) (F−1) (1,0)=
(1,0)=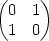 b) (F−1)
b) (F−1) (−2,4)=
(−2,4)=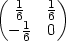 c) (F−1)
c) (F−1) (1,2)=
(1,2)=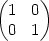 7.2 a) [x,y]
7.2 a) [x,y]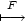
![[x(b2−-a2)−2a(by+c) y(a2−b2)−-2b(ax+c)] a2+b2 , a2+b2](diferencialni-pocet1958x.png) b) [x,y]
b) [x,y]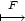
![[ ] ---y--- ---x--- √x2+y2-,√x2+y2-](diferencialni-pocet1960x.png) c) [x,y,z
]
c) [x,y,z
]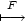
![[x √x2+y2+z2 y√x2+y2+z2- ] --√-2--2--,--√--2--2-,0 x +y x+y](diferencialni-pocet1962x.png) d) [x,y,z]
d) [x,y,z]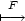
![[ ] rxR,ryR-, zrR](diferencialni-pocet1964x.png) , kde
r =
, kde
r = 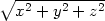 , R =
, R =
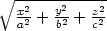 . 7.3 r
. 7.3 r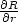 (r,
(r,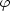 ) = R(r,
) = R(r,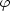 )
) (r,
(r,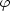 ),
), 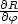 (r,
(r,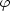 ) = −rR(r,
) = −rR(r,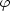 )
)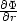 (r,
(r,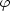 )
)
8.1
a) [2,2],[−2,−2]
b) body osy y c) body
roviny z = 0 ležící na elipse 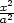 +
+ 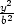 = 1. 8.2 a) y
= 1. 8.2 a) y =
= 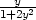 b) y
b) y =
= 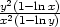 .
8.3 a) 5y
+ 2x =
0, y = −2x
b) 2x −
y +
1 = 0, 2x
− y −
1. 8.4 [1,1], [1,−3]
8.5 y
.
8.3 a) 5y
+ 2x =
0, y = −2x
b) 2x −
y +
1 = 0, 2x
− y −
1. 8.4 [1,1], [1,−3]
8.5 y
 = −(1
− ccosy)−3csiny.
8.6 a) tečná rovina:
x − 3y
− 4z
− 4
= 0, normála: x
= 2 +
= −(1
− ccosy)−3csiny.
8.6 a) tečná rovina:
x − 3y
− 4z
− 4
= 0, normála: x
= 2 + 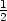 t, y =
t, y = 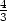 −
−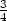 t, z = −1
− t, t
t, z = −1
− t, t 
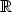 b) x + 4y
+ 6z −
21 = 0, x +
4y + 6z
+ 21 = 0 c) x −
y +
2z
b) x + 4y
+ 6z −
21 = 0, x +
4y + 6z
+ 21 = 0 c) x −
y +
2z 
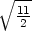 = 0.
8.7 a) zx
= zy
= −1,
zxx =
zxy =
zyy = 0
b) zx =
= 0.
8.7 a) zx
= zy
= −1,
zxx =
zxy =
zyy = 0
b) zx =
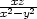 , zy
= −
, zy
= −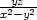 , zxx
= −
, zxx
= −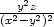 , zxy
=
, zxy
= 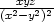 , zyy
= −
, zyy
= −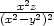 . 8.8 ymin
= 0,5
v x = 0, ymax
= −2
v x = 0,5.
8.9 a) zmin
= −2
v [1,−1],
zmax = 6
v [1,−1]
b) zmin = 1
v [−2,0],
zmax =
−
. 8.8 ymin
= 0,5
v x = 0, ymax
= −2
v x = 0,5.
8.9 a) zmin
= −2
v [1,−1],
zmax = 6
v [1,−1]
b) zmin = 1
v [−2,0],
zmax =
−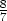 v [
v [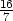 ,0].
,0].
9.1
a) fmax =
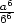 b) fmax
=
b) fmax
= 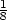 v [
v [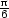 ,
,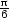 ,
,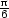 ]
c) fmin =
−
]
c) fmin =
−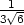 v [
v [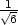 ,
,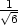 ,−
,−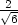 ], [
], [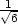 ,−
,−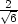 ,
,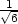 ], [−
], [−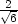 ,
,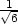 ,
,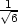 ], fmax
=
], fmax
= 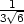 v [−
v [−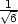 ,−
,−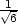 ,
,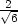 ], [−
], [−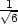 ,
,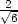 ,−
,−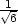 ], [
], [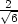 ,−
,−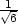 ,−
,−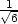 ] d) fmax
= 2 v [1,1,1]
e) fmin =
] d) fmax
= 2 v [1,1,1]
e) fmin =
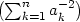 −1 pro
xi =
ai−1
−1 pro
xi =
ai−1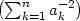 −1 f) fmin
=
−1 f) fmin
= 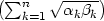 2 pro
xi =
2 pro
xi =
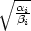
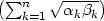 −1 g) fmax
nastává pro xi =
−1 g) fmax
nastává pro xi =
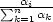 . 9.2
a) Délky hran hranolu:
. 9.2
a) Délky hran hranolu: 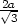 ,
,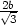 ,
,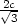 , V max
=
, V max
= 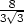 abc b) Rozměry
kvádru a,b,
abc b) Rozměry
kvádru a,b,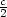 , V
max =
, V
max = 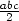 c) Výška hranolu
vhr =
c) Výška hranolu
vhr =  h, hrana základny a =
h, hrana základny a =
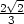 R,
V max =
R,
V max =
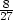 R2h
d) a = b
= c =
R2h
d) a = b
= c =
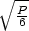 , V max =
, V max =
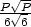 e) [x,y] =
e) [x,y] =
![----- ∘ ---- [ ∘ aa+b -b-] ±a , ± b a+b](diferencialni-pocet2028x.png) , f) Normála k elipsoidu v hledaném bodě
musí být kolmá na přímku spojující zadané dva body. 9.3 a) fmin
=
, f) Normála k elipsoidu v hledaném bodě
musí být kolmá na přímku spojující zadané dva body. 9.3 a) fmin
= 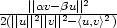 b) Nechť B
= (u1,…,un−1), je
matice sestavená z vektorů u1,…,un−1,
b) Nechť B
= (u1,…,un−1), je
matice sestavená z vektorů u1,…,un−1,  = (
= ( 1,…,
1,…, n−1),
fmin =
n−1),
fmin =
 (BT
B)−1
(BT
B)−1 ,
,
 pro
x = B(BT
B)−1
pro
x = B(BT
B)−1 .
.
[Další] [Předchozí] [Předchozí – na konec] [Na začátek] [Výše]