 2 do
2 do
 2
2[Další] [Předchozí] [Předchozí – na konec] [Na konec] [Výše]
V této kapitole využijeme výsledků předcházejících částí ke studiu vlastností zobrazení mezi prostory vyšších dimenzí. Výsledky, které zde odvodíme, hrají důležitou roli mj. v teorii integrálu funkcí více proměnných, a to při důkazu věty o substituci ve vícerozměrném integrálu, viz [R2].
 2 do
2 do
 2
2|
Definice 7.1. Nechť
jsou dány funkce
f,g dvou
proměnných a ![[x,y]↦−F→ [f(x,y),g(x,y)].](diferencialni-pocet755x.png)
|
Příklad 7.1. Vypište
složky
zobrazení pro stejnolehlost se středem
v počátku soustavy souřadnic,
otočení o úhel 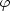 a pro kruhovou
inverzi určenou jednotkovou
kružnicí.
a pro kruhovou
inverzi určenou jednotkovou
kružnicí.
Řešení. i) Stejnolehlost se středem v počátku. Je-li k koeficient stejnolehlosti, pak
![F [x,y]↦−→ [kx,ky].](diferencialni-pocet756x.png)
ii) Otočení o úhel 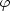
 [0, p] v kladném
smyslu. Pro odchylku
[0, p] v kladném
smyslu. Pro odchylku
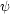 dvou
přímek procházejících
počátkem a bodem
[x1,y1], resp. [x2,y2] platí
dvou
přímek procházejících
počátkem a bodem
[x1,y1], resp. [x2,y2] platí
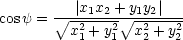
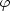 kolem
počátku
v kladném smyslu (tj. proti
směru
otáčení hodinových ručiček), je tvaru
kolem
počátku
v kladném smyslu (tj. proti
směru
otáčení hodinových ručiček), je tvaru
![F [x,y]↦−→ [xcosϕ − ysin ϕ,xsinϕ + ycosϕ].](diferencialni-pocet758x.png)
iii) Kruhová
inverze určená jednotkovou
kružnicí. Při tomto zobrazení
je bodu [x,y] přiřazen bod
[u,v] ležící na
polopřímce
určené počátkem a bodem
[x,y] s vlastností, že
součin vzdáleností
bodů
[x,y] a [u,v] od počátku je roven 1. Protože [x,y] a [u,v] leží na stejné
polopřímce, existuje reálné  > 0 takové, že u =
> 0 takové, že u =  x,
v =
x,
v =  y. Z podmínky na
vzdálenost bodů
[x,y] [u,v] od počátku dostáváme
y. Z podmínky na
vzdálenost bodů
[x,y] [u,v] od počátku dostáváme 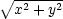
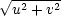 =
=
 (x2
+ y2) = 1, odtud
(x2
+ y2) = 1, odtud  = (x2 + y2)−1. Toto zobrazení
je proto
tvaru
= (x2 + y2)−1. Toto zobrazení
je proto
tvaru
![[x,y]↦−F→ [--x---,---y--]. x2 + y2 x2 + y2](diferencialni-pocet761x.png)
Příklad 7.2. Zobrazení množiny komplexních čísel do sebe lze chápat také
jako zobrazení z  2 do
2 do
 2.
Například
zobrazení, které
komplexnímu číslu z = x + iy přiřadí jeho druhou mocninu z2, definuje
zobrazení
2.
Například
zobrazení, které
komplexnímu číslu z = x + iy přiřadí jeho druhou mocninu z2, definuje
zobrazení
![F [x,y]↦−→ [x2 − y2,2xy],](diferencialni-pocet762x.png)
|
Definice 7.2. Řekneme,
že
zobrazení F = {f,g} z Řekneme, že F je diferencovatelné
v bodě
[x0,y0], jestliže každá z funkcí
f,g je
diferencovatelná v bodě
[x0,y0]. Zobrazení
dF(x0,y0) :
|
Podle
této
definice je tedy diferenciál
zobrazení F
lineární zobrazení
z  2 do
2 do
 2.
Protože z lineární algebry
víme, že každé lineární zobrazení
mezi konečně dimenzionálními prostory lze
reprezentovat vhodnou maticí, dostáváme se k následující definici.
2.
Protože z lineární algebry
víme, že každé lineární zobrazení
mezi konečně dimenzionálními prostory lze
reprezentovat vhodnou maticí, dostáváme se k následující definici.
Nejprve odvodíme vzorec pro diferenciál složeného zobrazení. Je zcela analogický vztahu pro derivaci složené funkce jedné proměnné, stačí „zapomenout“, že místo zobrazení mezi jednodimenzionálními prostory se jedná o vícerozměrná zobrazení.
Věta 7.1. Nechť
F =
{f1,f2}, G = {g1,g2} jsou zobrazení
z  2 do
2 do
 2. Pak pro
Jacobiho1 matici
složeného zobrazení
H =
F
2. Pak pro
Jacobiho1 matici
složeného zobrazení
H =
F  G platí
G platí
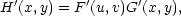 |
(7.2) |
kde [u,v] = G(x,y), tj. u = g1(x,y), v = g2(x,y). Pro jejich jacobiány
dostáváme detH (x,y) = detF
(x,y) = detF (u,v)detG
(u,v)detG (x,y).
(x,y).
Důkaz. Nechť h1,h2 jsou souřadnicové funkce zobrazení H, tj.
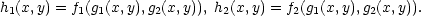 |
(7.3) |
Aplikací Věty 5.1 dostáváme
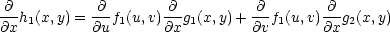 |
(7.4) |
a podle Definice 7.3
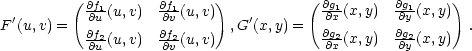
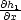 (x,y), kde h1
je dáno v (7.3
).
Stejným způsobem ověříme, že i ostatní
prvky součinu matic
F
(x,y), kde h1
je dáno v (7.3
).
Stejným způsobem ověříme, že i ostatní
prvky součinu matic
F
 G
G jsou
totožné s výrazy pro
prvky matice H
získané pomocí
(7.2
), čímž je rovnost (7.2
)
dokázána. Vzorec pro jacobiány plyne
z faktu, že determinant
součinu dvou matic je roven součinu determinantů. □
jsou
totožné s výrazy pro
prvky matice H
získané pomocí
(7.2
), čímž je rovnost (7.2
)
dokázána. Vzorec pro jacobiány plyne
z faktu, že determinant
součinu dvou matic je roven součinu determinantů. □
V diferenciálním počtu
funkcí jedné
proměnné jsme
vyšetřovali lokální vlastnosti funkce (tj. v okolí
daného bodu)
pomocí derivace funkce v tomto
bodě (což je pro funkci jedné proměnné v podstatě
ekvivalentní diferenciálu této funkce,
neboť funkce f
: 

 je
v nějakém
bodě diferencovatelná, právě když zde existuje
konečná derivace f
je
v nějakém
bodě diferencovatelná, právě když zde existuje
konečná derivace f ).
Podobně budeme postupovat v případě zobrazení
mezi prostory vyšších dimenzí.
).
Podobně budeme postupovat v případě zobrazení
mezi prostory vyšších dimenzí.
Věta 7.2. Předpokládejme,
že
složky zobrazení F
= {f,g} :  2
2

 2 mají v bodě
[x0,y0] spojité
parciální derivace
prvního řádu a Jacobiho
matice F
2 mají v bodě
[x0,y0] spojité
parciální derivace
prvního řádu a Jacobiho
matice F (x0,y0) je regulární, tj.
detF
(x0,y0) je regulární, tj.
detF (x0,y0)≠0. Pak existuje okolí
(x0,y0)≠0. Pak existuje okolí  bodu [x0,y0], v němž je
zobrazení F prosté, a pro Jacobiho matici inverzního
zobrazení F−1 v bodě
[u0,v0] = F(x0,y0) platí
bodu [x0,y0], v němž je
zobrazení F prosté, a pro Jacobiho matici inverzního
zobrazení F−1 v bodě
[u0,v0] = F(x0,y0) platí
![(F −1)′(u0,v0) = [F ′(x0,y0)]−1.](diferencialni-pocet770x.png) |
(7.5) |
Důkaz.
Tvrzení zde nebudeme dokazovat
se všemi podrobnostmi (detailní důkaz je proveden v [R1]).
Zdůrazněme zde pouze hlavní myšlenku
důkazu. Diferenciál dF(x0,y0) zobrazení
F :
 2
2

 2 je
nejlepší lineární aproximace F
v okolí
bodu [x0,y0]. Je-li zobrazení
dF(x0,y0) prosté – to nastane,
právě když je jeho matice F
2 je
nejlepší lineární aproximace F
v okolí
bodu [x0,y0]. Je-li zobrazení
dF(x0,y0) prosté – to nastane,
právě když je jeho matice F (x0,y0) regulární – je
v jistém
okolí bodu [x0,y0] prosté
i samo zobrazení F.
(x0,y0) regulární – je
v jistém
okolí bodu [x0,y0] prosté
i samo zobrazení F.
Vztah (7.5
)
dokážeme takto: Z definice inverzního
zobrazení je F−1(F(x,y)) = [x,y]. Položme [u,v] = F(x,y). Ze vztahu pro Jacobiho
matici složeného
zobrazení plyne (F−1) (u,v)F
(u,v)F (x,y) = E – jednotková matice (neboť
Jacobiho matice identického
zobrazení je jednotková
matice) a odtud (F−1)
(x,y) = E – jednotková matice (neboť
Jacobiho matice identického
zobrazení je jednotková
matice) a odtud (F−1) (u,v) = [F
(u,v) = [F (x,y)]−1. □
(x,y)]−1. □
Příklad 7.3. i)
Rozhodněte, zda
zobrazení F = {f,g} :  2
2

 2 se
souřadnicovými funkcemi
f(x,y) = xy, g(x,y) =
2 se
souřadnicovými funkcemi
f(x,y) = xy, g(x,y) = 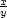 je
prosté v okolí
bodu [x,y] = [2,1]. Pokud ano,
určete Jacobiho matici inverzního
zobrazení v bodě
[u,v] = F(2,1).
je
prosté v okolí
bodu [x,y] = [2,1]. Pokud ano,
určete Jacobiho matici inverzního
zobrazení v bodě
[u,v] = F(2,1).
Řešení. Jacobiho matice zobrazení F je
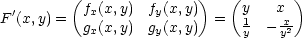
 (2,1) = −4, tedy F
je prosté v jistém okolí
bodu [2,1]. Pro Jacobiho matici
inverzního zobrazení
F−1 v bodě
[2,2] = F(2,1) platí
(2,1) = −4, tedy F
je prosté v jistém okolí
bodu [2,1]. Pro Jacobiho matici
inverzního zobrazení
F−1 v bodě
[2,2] = F(2,1) platí
![( ) −1 ( ) (F −1)′(2,2) = [F ′(2,1)]−1 = 1 2 = 12 12 . 1 − 2 14 − 14](diferencialni-pocet773x.png)
ii) Určete Jacobiho matici
zobrazení F :  2
2

 2,
které je složením kruhové
inverze, jejíž řídicí kružnice je jednotková, a
otočení o úhel
2,
které je složením kruhové
inverze, jejíž řídicí kružnice je jednotková, a
otočení o úhel 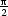 v kladném smyslu,
přičemž nejprve se provádí kruhová
inverze.
v kladném smyslu,
přičemž nejprve se provádí kruhová
inverze.
Řešení. Kruhová
inverze přiřadí bodu
[x,y] bod [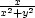 ,
,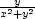 ] a otočení o úhel
] a otočení o úhel 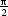 v kladném smyslu
přiřadí bodu [x,y] bod [−y,x], viz příklad 7.1. Složené zobrazení
tedy přiřadí bodu
[x,y] bod [−
v kladném smyslu
přiřadí bodu [x,y] bod [−y,x], viz příklad 7.1. Složené zobrazení
tedy přiřadí bodu
[x,y] bod [−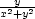 ,
,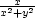 ]. Jacobiho
matice tohoto zobrazení
je
]. Jacobiho
matice tohoto zobrazení
je
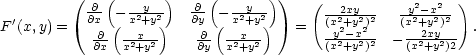
Poznámka 7.1. i)
Jacobiho matici inverzního
zobrazení v Příkladu 7.3, část i) můžeme vypočíst také
přímo –
prostřednictvím explicitního
vyjádření inverzního
zobrazení k F. Vypočteme-li
z rovnic u = xy, v =  proměnné x a y pomocí
u a
v,
dostáváme
proměnné x a y pomocí
u a
v,
dostáváme
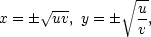
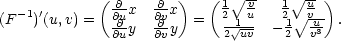
ii) Ze
skutečnosti, že detF (x0,y0) = 0
pro nějaké zobrazení
F :
(x0,y0) = 0
pro nějaké zobrazení
F :
 2
2

 2 ještě neplyne, že F není prosté
v okolí
bodu [x0,y0], tj. podmínka detF
2 ještě neplyne, že F není prosté
v okolí
bodu [x0,y0], tj. podmínka detF (x0,y0)≠0 je pouze dostatečná, nikoliv
nutná pro to, aby zobrazení
F bylo
prosté v okolí
bodu [x0,y0]. Například zobrazení
F dané předpisem
(x0,y0)≠0 je pouze dostatečná, nikoliv
nutná pro to, aby zobrazení
F bylo
prosté v okolí
bodu [x0,y0]. Například zobrazení
F dané předpisem
![F [x,y]↦−→ [x3,y3]](diferencialni-pocet784x.png)
 2 na
2 na
 2,
přestože detF
2,
přestože detF (0,0) = 0.
(0,0) = 0.
 n do
n do
 m
mPro
zobrazení mezi prostory dimenzí vyšších
než dvě je situace zcela analogická. Jsou-li
n,m 
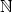 a f1,…,fm :
a f1,…,fm :  n
n

 , pak
přiřazení
, pak
přiřazení
![F [x1,...,xn]↦−→ [f1(x1,...,xn),...,fm(x1,...,xn)]](diferencialni-pocet785x.png)
 n
n 
 m. Funkce
f1,…,fm se
nazývají složky nebo
souřadnicové
funkce zobrazení
F. Jsou-li
všechny složky
spojité v bodě
x∗,
řekneme, že F je spojité
v bodě
x∗. Jsou-li
f1,…,fn diferencovatelné
v bodě
x∗
m. Funkce
f1,…,fm se
nazývají složky nebo
souřadnicové
funkce zobrazení
F. Jsou-li
všechny složky
spojité v bodě
x∗,
řekneme, že F je spojité
v bodě
x∗. Jsou-li
f1,…,fn diferencovatelné
v bodě
x∗
 n,
řekneme, že
zobrazení F je diferencovatelné
v bodě
x∗. Jeho
diferenciál dF(x∗) definujeme jako lineární zobrazení
z
n,
řekneme, že
zobrazení F je diferencovatelné
v bodě
x∗. Jeho
diferenciál dF(x∗) definujeme jako lineární zobrazení
z  n do
n do
 m
dané
předpisem
m
dané
předpisem
![dF h = [h1,...,hn]↦−→ [df1(x∗)(h),...,dfm(x ∗)(h)],](diferencialni-pocet786x.png)
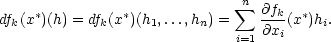
 n)
n)
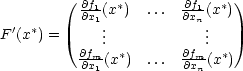 |
(7.6) |
se nazývá Jacobiho matice nebo také derivace zobrazení F a v případě n = m se její determinant nazývá jacobián zobrazení F v bodě x∗. V některé starší literatuře se jacobián značí
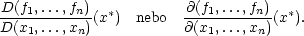
Věta 7.3. Nechť
zobrazení G :  n
n 
 m
je diferencovatelné v bodě
x∗
m
je diferencovatelné v bodě
x∗
 n
a zobrazení F :
n
a zobrazení F :  m
m 
 k
je diferencovatelné v bodě
y∗ = G(x∗). Pak složené zobrazení
H =
F
k
je diferencovatelné v bodě
y∗ = G(x∗). Pak složené zobrazení
H =
F  G :
G :  n
n

 k je
diferencovatelné v bodě
x∗ a
platí
k je
diferencovatelné v bodě
x∗ a
platí
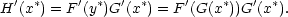 |
(7.7) |
Je-li n = m a detG (x∗)≠0, existuje okolí
bodu x∗,
v němž je
zobrazení G prosté,
tj. existuje zde
inverzní zobrazení
G−1 a pro jeho Jacobiho matici v bodě
y∗ = G(x∗) platí
(x∗)≠0, existuje okolí
bodu x∗,
v němž je
zobrazení G prosté,
tj. existuje zde
inverzní zobrazení
G−1 a pro jeho Jacobiho matici v bodě
y∗ = G(x∗) platí
![−1′ ∗ ′ ∗ − 1 (G )(y ) = [G (x )] .](diferencialni-pocet791x.png) |
(7.8) |
Poznámka 7.2. Vzorce (7.7
)
a (7.8) pro Jacobiho matici
složeného zobrazení a
Jacobiho matici inverzního
zobrazení jsou
formálně zcela stejné
jako vzorce pro derivaci
složené a inverzní
funkce jedné proměnné, zde
však
musíme dávat pozor na pořadí obou
činitelů,
neboť násobení
matic není komutativní
operace. Matice F je typu
k
je typu
k  m, G
m, G je
typu m
je
typu m  n,
násobení
těchto matic je tedy
možné pouze v pořadí uvedeném v (7.7
)
(tímto
způsobem se také
pořadí činitelů
nejlépe pamatuje).
n,
násobení
těchto matic je tedy
možné pouze v pořadí uvedeném v (7.7
)
(tímto
způsobem se také
pořadí činitelů
nejlépe pamatuje).
Příklad 7.4. Vypočtěte
Jacobiho matici zobrazení F :  3
3 
 3,
které bodu [x,y,z] přiřadí jeho sférické souřadnice
3,
které bodu [x,y,z] přiřadí jeho sférické souřadnice
![∘ ----------- ∘ -2---2- [x,y,z]↦−F→ [ x2 + y2 + z2,arctg y,arctg-x-+-y-]. x z](diferencialni-pocet792x.png)
F (x,y,z) = (x,y,z) = |
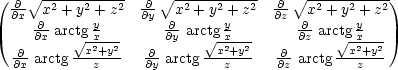 = = |
||
| = | 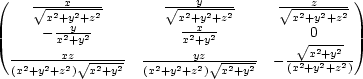 . . |
ii) Jak jsme
již poznamenali v Příkladu 7.2, zobrazení
F :

 množiny komplexních čísel do sebe můžeme chápat jako
zobrazení z
množiny komplexních čísel do sebe můžeme chápat jako
zobrazení z  2 do
2 do
 2,
které komplexnímu číslu z = x + iy přiřadí číslo F(z) = f(x,y) + ig(x,y), kde f,g jsou
reálné funkce dvou proměnných.
Podobně jako v reálném oboru definujeme
derivaci komplexní
funkce F v čísle z0
= x0
+ iy0
vztahem
2,
které komplexnímu číslu z = x + iy přiřadí číslo F(z) = f(x,y) + ig(x,y), kde f,g jsou
reálné funkce dvou proměnných.
Podobně jako v reálném oboru definujeme
derivaci komplexní
funkce F v čísle z0
= x0
+ iy0
vztahem
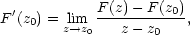
 > 0 existuje
> 0 existuje 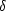 > 0 takové, že pro všechna
z splňující 0 <
> 0 takové, že pro všechna
z splňující 0 <  z − z0
z − z0 <
< 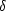 platí
platí
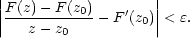
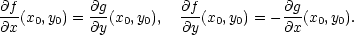
Řešení. Označme F (z0) = A + iB. Z diferencovatelnosti funkcí f,g v bodě
[x0,y0] plyne
(z0) = A + iB. Z diferencovatelnosti funkcí f,g v bodě
[x0,y0] plyne
![0 = lim F-(z)-− F-(z0) − F′(z ) = z→z0 z − z0 0 f-(x,y)+-ig(x,y)−-[f(x0,y0)+-ig(x0,y0)] = (x,y)li→m(x0,y0) (x − x0)+ i(y − y0) − (A + iB) = f(x,y)− f(x ,y )− A(x − x )+ B(y − y ) = lim -----------0-0----------0---------0-+ (x,y)→(x0,y0) (x − x0)+ i(y − y0) +i lim g(x,y)−-g(x0,y0)−-B(x-−-x0)−-A(y−-y0) = (x,y)→(x0,y0) (x − x0)+ i(y − y0) (fx(x0,y0)−-A)(x−-x0)+-(fy(x0,y0)+-B)(y-− y0) = (x,y)l→im(x0,y0) ∘(x-−-x0)2 +-(y−-y0)2 + +i lim (gx(x0,y0)-− B)∘(x-−-x0)+-(gy(x0,y0)−-A)(y−-y0). (x,y)→(x0,y0) (x− x0)2 + (y− y0)2](diferencialni-pocet798x.png)
|
V odstavci 4.1 jsme uvedli, že ve
fyzikální terminologii a také v některých odvětvích matematiky, např. v numerických
metodách, se vektor parciálních derivací
f funkce f
nazývá gradient funkce
a
značí se gradf.
funkce f
nazývá gradient funkce
a
značí se gradf.
Zobrazení
F :
 3
3

 3 se ve
fyzikální terminologii nazývá vektorové
pole. Lze je chápat jako
zobrazení, které
bodu o souřadnicí
ch [x,y,z] přiřadí vektor s počátečním bodem v počátku a koncovým bodem
3 se ve
fyzikální terminologii nazývá vektorové
pole. Lze je chápat jako
zobrazení, které
bodu o souřadnicí
ch [x,y,z] přiřadí vektor s počátečním bodem v počátku a koncovým bodem
![F (x,y,z) = [P (x,y,z),Q(x,y,z),R(x,y,z)],](diferencialni-pocet799x.png)
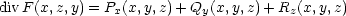
![rotF(x,z,y) = [Ry(x,y,z)− Qz(x,y,z), Pz(x,y,z)− Rx(x,y,z),Qx(x,y,z)− Py(x,y,z)]](diferencialni-pocet801x.png)
|
Příklad 7.5. Vypočtěte divergenci a rotaci gravitačního pole vytvořené hmotným bodem o jednotkové hmotnosti umístěným v počátku souřadné soustavy.
Řešení. Z fyziky je známo, že dva
hmotné body o hmotnostech m1,m2
se navzájem přitahuj
í silou, jejíž velikost je  F
F =
=
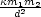 , kde
, kde  = 6,67
= 6,67  10−11 Nm2/kg2
je Newtonova gravitační konstanta a
d je
vzdálenost bodů. Bod [x,y,z] s jednotkovou
hmotností bude přitahován do
počátku silou, jejíž směr je opačný než směr vektoru
s počátkem v [0,0,0] a koncem v [x,y,z] a jehož
velikost
10−11 Nm2/kg2
je Newtonova gravitační konstanta a
d je
vzdálenost bodů. Bod [x,y,z] s jednotkovou
hmotností bude přitahován do
počátku silou, jejíž směr je opačný než směr vektoru
s počátkem v [0,0,0] a koncem v [x,y,z] a jehož
velikost  F
F je rovna
je rovna
 (x2
+ y2
+ z2)−1. Tedy
F(x,y,z) = −
(x2
+ y2
+ z2)−1. Tedy
F(x,y,z) = − [x,y,z] a hodnotu
skaláru
[x,y,z] a hodnotu
skaláru  určíme z podmínky pro velikost
F,
tj.
určíme z podmínky pro velikost
F,
tj. 
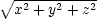 =
=  (x2
+ y2
+ z2)−1,
a tedy
(x2
+ y2
+ z2)−1,
a tedy  =
=  (x2 + y2
+ z2)−
(x2 + y2
+ z2)−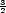 . Odtud
. Odtud
![[ x y z ] F(x,y,z) = [P(x,y,z),Q(x,y,z),R(x,y,z)] = κ − r3,− r3,− r3 ,](diferencialni-pocet805x.png)
|
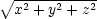 . Nyní vypočteme všechny
parciální derivace funkcí
P,Q,R potřebné k určení div F a rotF.
. Nyní vypočteme všechny
parciální derivace funkcí
P,Q,R potřebné k určení div F a rotF.
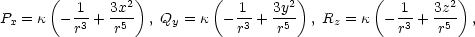
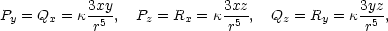
Manipulace
s diferenciálními výrazy
obsahujícími operátory rotace a
divergence se podstatně usnadňuje
zavedením tzv. Hamiltonova nabla
operátoru 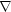 .3
Tento symbol je formálně definován jako
vektorový operátor předpisem
.3
Tento symbol je formálně definován jako
vektorový operátor předpisem
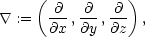
 3
3

 přiřazuje vektorové
pole
přiřazuje vektorové
pole
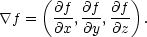
 ,
které diferencovatelné
funkci f přiřazuje
její derivaci. Operátor
,
které diferencovatelné
funkci f přiřazuje
její derivaci. Operátor 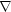 lze
s výhodou
použít i
při formalizaci
operátorů divergence a rotace. Uvažujme nejprve
případ divergenčního
operátoru. Formálně můžeme aplikaci operátoru divergence
na pole F zapsat takto:
lze
s výhodou
použít i
při formalizaci
operátorů divergence a rotace. Uvažujme nejprve
případ divergenčního
operátoru. Formálně můžeme aplikaci operátoru divergence
na pole F zapsat takto:
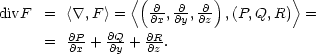 |
(7.9) |
Podobně můžeme formalizovat operátor rotace rot pomocí vektorového součinu takto:
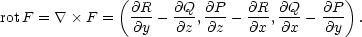
 v
dvou vektorů u = (u1,u2,u3), v = (v1,v2,v3) je definován jako vektor
kolmý na lineární prostor
generovaný dvojicí
vektorů u,v, orientovaný
podle pravidla pravé ruky, a
délky
v
dvou vektorů u = (u1,u2,u3), v = (v1,v2,v3) je definován jako vektor
kolmý na lineární prostor
generovaný dvojicí
vektorů u,v, orientovaný
podle pravidla pravé ruky, a
délky
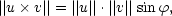
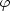 je úhel mezi vektory u,v.
Konkrétně, souřadnice vektoru
u
je úhel mezi vektory u,v.
Konkrétně, souřadnice vektoru
u  v jsou
v jsou
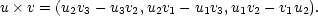
 v = 0. Proto pro
složení operátorů rotace a gradientu platí
v = 0. Proto pro
složení operátorů rotace a gradientu platí
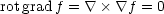
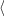 u,u
u,u  v
v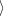 =
0, neboť vektor
u
=
0, neboť vektor
u  v je
kolmý na každý z vektorů
u,v.
Proto
v je
kolmý na každý z vektorů
u,v.
Proto
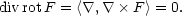
Na závěr této kapitoly připomeňme ještě pojem Laplaceova operátoru Δ, který je definován předpisem
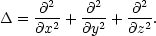
 můžeme
Laplaceův operátor definovat
takto:
můžeme
Laplaceův operátor definovat
takto:
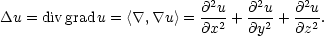
Cvičení 
7.1. Rozhodněte, zda zobrazení F = {f,g} je prosté v okolí bodu [x0,y0]. Pokud ano, určete Jacobiho matici inverzního zobrazení v bodě [u0,v0] = F(x0,y0).
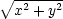 , g(x,y) = xy, [x0,y0] =
[0,1]
, g(x,y) = xy, [x0,y0] =
[0,1]
7.2. Určete souřadnicové
funkce a Jacobiho matici
uvedených zobrazení:
a) Osová souměrnost podle přímky p, jejíž rovnice je ax
+ by
+ c
= 0.
b) Složení osové
souměrnosti podle
přímky y = x a projekce bodu
na jednotkovou
kružnici (bodu [x,y]≠[0,0] je přiřazen bod na
jednotkové kružnici, který
je průsečíkem kružnice
s přímkou určenou
počátkem a bodem
[x,y]).
c) Bodu [x,y,z] 
 3 je
přiřazen bod ležící na rovníku
kulové plochy se středem v počátku procházející bodem
[x,y,z], přičemž přiřazený
bod leží na
stejném poledníku.
3 je
přiřazen bod ležící na rovníku
kulové plochy se středem v počátku procházející bodem
[x,y,z], přičemž přiřazený
bod leží na
stejném poledníku.
d) „Eliptická inverze
v  3“: Bodu
[x,y,z] je přiřazen bod ležící na polopřímce určené počátkem a bodem [x,y,z], přičemž součin vzdálenosti vzoru a obrazu od počátku je roven vzdálenosti od
počátku průsečíku jejich spojnice
s elipsoidem
3“: Bodu
[x,y,z] je přiřazen bod ležící na polopřímce určené počátkem a bodem [x,y,z], přičemž součin vzdálenosti vzoru a obrazu od počátku je roven vzdálenosti od
počátku průsečíku jejich spojnice
s elipsoidem 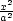 +
+ 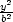 +
+ 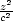 = 1.
= 1.
7.3. Je
dána
dvojice diferencovatelných
funkcí R(r,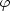 ),Φ(r,
),Φ(r,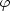 ), která
definuje funkci F
:
), která
definuje funkci F
: 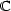

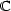 předpisem
předpisem
7.4. Dokažte následují
identity (buď přímým derivováním, nebo
pomocí operátoru 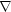 ). V těchto
identitách f :
). V těchto
identitách f :  3
3 
 a F,G :
a F,G :  3
3

 3.
3.
 F,gradf
F,gradf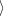 +
f div
F,
+
f div
F,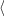 gradf,F
gradf,F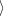 ,
, G) =
G) =
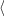 rotA,B
rotA,B −
− A,rotB
A,rotB ,
,
∗
Důležité je nepřestat se ptát. Zvědavost existuje z dobrého důvodu. Nelze než žasnout, rozvažujeme-li o tajemstvích věčnosti, života a úžasného uspořádání věcí vezdejších. Stačí, když se člověk snaží každý den porozumět alespoň kousku tohoto tajemství. Nikdy neztrácejte zvědavost, tu posvátnou vlastnost. (A. Einstein)
∗
1Carl Jacobi (1804–1851), německý matematik
2Augustin Louis Cauchy (1789–1857), francouzský matematik, Bernhard Riemann (1826 až 1866), německý matematik, oba jsou považováni za spolutvůrce moderní matematiky.
3William Rowan Hamilton (1805–1865), irský matematik. Termín nabla operátor byl zaveden přímo Hamiltonem, nabla označuje starý hudební nástroj trojúhelníkového tvaru.
[Další] [Předchozí] [Předchozí – na konec] [Na začátek] [Výše]