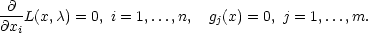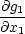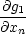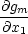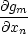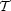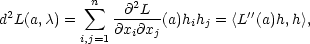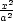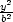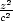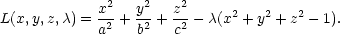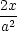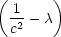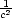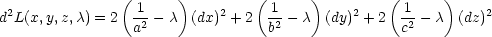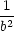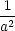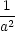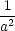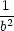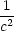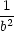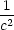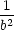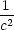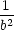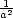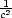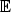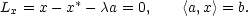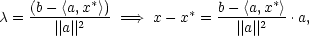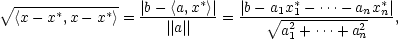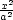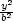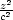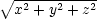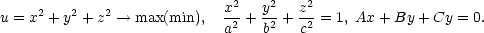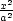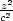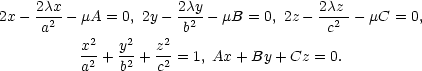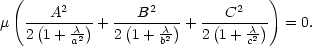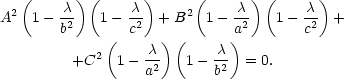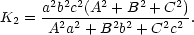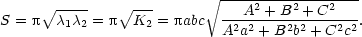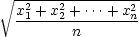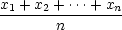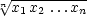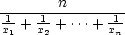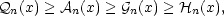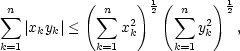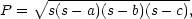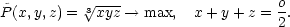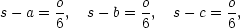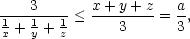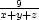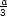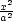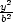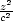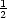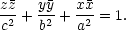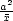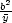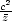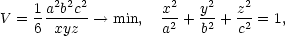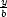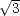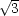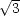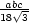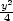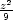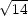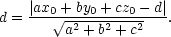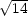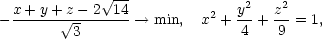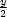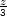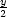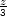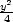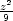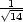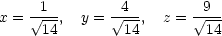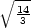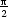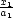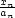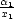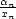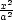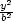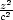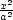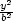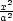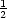Kapitola 9
Vázané extrémy
V úvodu
Kapitoly 6 jsme zdůraznili,
že
vyšetřování extrémů funkcí
je jednou
z nejdůležitějších částí diferenciálního
počtu. V předchozích dvou kapitolách jsme si
připravili aparát k tomu, abychom mohli vyšetřovat tzv.
vázané extrémy. Je to vlastně
v jistém smyslu
speciální případ lokálních extrémů, avšak metody
uvedené v Kapitole 6 zde nejsou vhodné. V prvním odstavci
vysvětlíme tzv. metodu Lagrangeových
multiplikátorů, kde extrémy původní
funkce vyšetřujeme
pomocí přiřazené, tzv. Lagrangeovy funkce. Ve druhém odstavci studujeme
vázané extrémy pomocí
nerovností mezi
průměry čísel.
9.1 Metoda
Lagrangeových multiplikátorů
Začněme následující úlohou.
Určete
absolutní minimum a maximum funkce u = f(x,y,z) na množině M : x2
+ y2
+ z2
≤ 1, x,y,z ≥
0 (konkrétní tvar funkce
f není v tuto
chvíli podstatný).
Vyšetřujeme-li
při řešení úlohy funkci
f na
části hranice
tvořené kulovou plochou, vyjádříme z = 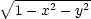 a
funkci f(x,y,
a
funkci f(x,y,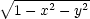 ) vyšetřujeme na množině M :
x2 + y2
≤ 1, x,y ≥
0, tj. najdeme
stacionární body uvnitř
M
a vyšetříme funkci na hranici množiny M. Provést toto na
části hranice
tvořené čtvrtkružnicí znamená
vyjádřit y =
) vyšetřujeme na množině M :
x2 + y2
≤ 1, x,y ≥
0, tj. najdeme
stacionární body uvnitř
M
a vyšetříme funkci na hranici množiny M. Provést toto na
části hranice
tvořené čtvrtkružnicí znamená
vyjádřit y = 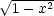 a dosadit
do f,
tj. vyšetřovat funkci f(x,
a dosadit
do f,
tj. vyšetřovat funkci f(x,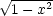 ,0) pro x
,0) pro x  [0,1].
[0,1].
Tímto postupem
převedeme původní problém vyšetření funkce na
hranici na studium extrémů funkce
jedné proměnné. Je zřejmé, že tato
metoda je nepraktická zejména při větším počtu
proměnných. V tomto
odstavci si popíšeme tzv. metodu Lagrangeových
multiplikátorů, která
řešení úlohy
podstatně usnadní.
V této kapitole se
zabýváme případem, kdy
množina M
je zadána systémem rovností
| g1(x1,…,xn) |
= 0 |
|
|
| g2(x1,…,xn) |
= 0 |
|
|
|
⋮ |
(9.1) |
| gm(x1,…,xn) |
= 0, |
|
|
kde 1
≤ m <
n. V tomto případě se často místo
termínu lokální extrém vzhledem
k M používá termín lokální extrém vázaný podmínkami (9.1
) nebo
prostě vázaný lokální extrém.
Nejprve zformulujme
nutnou podmínku pro existenci vázaného
extrému.
Věta 9.1. Nechť funkce n
proměnných f,g1,…,gm, 1 ≤ m <
n, mají spojité
parciální derivace 1.
řádu v otevřené množině U 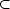
 n a
nechť v každém
bodě množiny U má matice
n a
nechť v každém
bodě množiny U má matice

|
(9.2) |
hodnost m. Buď
M množina všech
bodů [x1,…,xn], které
vyhovují rovnicím (9.1
). Má-li funkce
f v bodě
a =
[a1,…,an]  M lokální extrém vzhledem
k M,
existují reálná čísla
M lokální extrém vzhledem
k M,
existují reálná čísla  1,…,
1,…, m tak,
že jsou
splněny rovnosti
m tak,
že jsou
splněny rovnosti
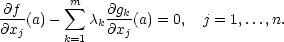
|
(9.3) |
Poznámka 9.1. i)
Dříve
než přistoupíme k důkazu
tvrzení, objasněme si
význam rovnosti (9.3
). Zprvu
uvažujme nejjednodušší případ n = 2,m = 1. Pak
M je
křivka v  2 zadaná
rovnicí g(x,y) = 0 (píšeme x,y, [x∗,y∗] a g místo x1,x2, a a g1).
Rovnost (9.3) můžeme psát ve tvaru rovnosti dvou dvojrozměrných
vektorů
2 zadaná
rovnicí g(x,y) = 0 (píšeme x,y, [x∗,y∗] a g místo x1,x2, a a g1).
Rovnost (9.3) můžeme psát ve tvaru rovnosti dvou dvojrozměrných
vektorů
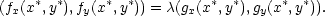 Když
si uvědomíme, že vektor
(gx(x∗,y∗),gy(x∗,y∗)) je normálovým vektorem ke křivce
g(x,y) = 0 v bodě
[x∗,y∗] a vektor (fx(x∗,y∗),fy(x∗,y∗)) je normálovým vektorem
k vrstevnici funkce
f na
úrovni c
= f(x∗,y∗), vztah (9.3
)
říká, že vektory
(fx(x∗,y∗),fy(x∗,y∗)) a (gx(x∗,y∗),gy(x∗,y∗)) jsou lineárně závislé.
Jinými slovy, křivky
g(x,y) = 0 a f(x,y) = f(x∗,y∗) mají společnou
tečnu
v bodě [x∗,y∗]. Tato skutečnost je
v plném souladu
s úvahami,
které jsme použili
při řešení Příkladů 6.6.
Když
si uvědomíme, že vektor
(gx(x∗,y∗),gy(x∗,y∗)) je normálovým vektorem ke křivce
g(x,y) = 0 v bodě
[x∗,y∗] a vektor (fx(x∗,y∗),fy(x∗,y∗)) je normálovým vektorem
k vrstevnici funkce
f na
úrovni c
= f(x∗,y∗), vztah (9.3
)
říká, že vektory
(fx(x∗,y∗),fy(x∗,y∗)) a (gx(x∗,y∗),gy(x∗,y∗)) jsou lineárně závislé.
Jinými slovy, křivky
g(x,y) = 0 a f(x,y) = f(x∗,y∗) mají společnou
tečnu
v bodě [x∗,y∗]. Tato skutečnost je
v plném souladu
s úvahami,
které jsme použili
při řešení Příkladů 6.6.
ii) V obecném případě nechť
f ,g
,g k jsou vektory
parciálních derivací
funkcí f,gk,
k =
1,…,m a nechť
M je
množina určená systémem (9.1
). Pak
v souladu s terminologií z kapitoly o implicitních funkcích
vztah (9.3) říká, že f
k jsou vektory
parciálních derivací
funkcí f,gk,
k =
1,…,m a nechť
M je
množina určená systémem (9.1
). Pak
v souladu s terminologií z kapitoly o implicitních funkcích
vztah (9.3) říká, že f (a)
(a) 
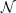 M(a), kde
M(a), kde 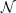 M(a) je normálový prostor
k M v bodě a.
M(a) je normálový prostor
k M v bodě a.
iii) Funkce
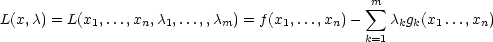 se nazývá Lagrangeova
funkce a konstanty
se nazývá Lagrangeova
funkce a konstanty  k Lagrangeovy
multiplikátory. Princip metody
Lagrangeových multiplikátorů spočívá v tom,
že
do Lagrangeovy funkce jsou
„zabudovány“ vazebné
podmínky a
místo vyšetřování funkce f
na M
vyšetřujeme Lagrangeovu
funkci L bez
omezujících podmínek. Metodu
multiplikátorů lze použít i v případě, kdy množina M
je zadána nikoliv jen
systémem rovností, ale i systémem
nerovností.
k Lagrangeovy
multiplikátory. Princip metody
Lagrangeových multiplikátorů spočívá v tom,
že
do Lagrangeovy funkce jsou
„zabudovány“ vazebné
podmínky a
místo vyšetřování funkce f
na M
vyšetřujeme Lagrangeovu
funkci L bez
omezujících podmínek. Metodu
multiplikátorů lze použít i v případě, kdy množina M
je zadána nikoliv jen
systémem rovností, ale i systémem
nerovností.
Důkaz Věty 9.1. Předpokládejme nejprve,
že
funkce gk
jsou afinní, tj.
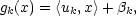 kde uk
kde uk

 n,
n,
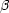 k
k

 ,
k =
1,…,m. Předpokládejme,
že
neexistuje m-tice multiplikátorů, pro
něž platí (9.3
), pak
f
,
k =
1,…,m. Předpokládejme,
že
neexistuje m-tice multiplikátorů, pro
něž platí (9.3
), pak
f (a)∉Lin{g
(a)∉Lin{g 1(a),…,g
1(a),…,g m(a)}. To znamená, že existuje
h
m(a)}. To znamená, že existuje
h 
 n,
h
n,
h  Lin{g
Lin{g 1(a),…,g
1(a),…,g m(a)}
m(a)} (
( značí ortogonální doplněk)
takové, že
značí ortogonální doplněk)
takové, že 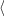 f
f (a),h
(a),h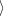 ≠0. Položme y = a +
≠0. Položme y = a +  h.
h.
Vzhledem
k tomu, že funkce
gk jsou
afinní a h  Lin{g
Lin{g 1(a),…,g
1(a),…,g m(a)}
m(a)} = Lin{u1,…,um}
= Lin{u1,…,um} , je
, je
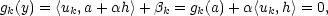 tedy y
tedy y
 M. Z diferencovatelnosti funkce f dostáváme
M. Z diferencovatelnosti funkce f dostáváme
![[ ] ′ ′ τ(αh) f(y) = f(a)+ α〈f(a),h〉+ τ(αh) = f(a)+ α 〈f (a),h 〉+ α ,](diferencialni-pocet942x.png) kde lim
kde lim
 0
0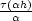 .
Odtud
.
Odtud
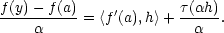 Je-li nyní např.
Je-li nyní např. 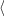 f
f (a),h
(a),h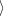 > 0, limitním přechodem pro
> 0, limitním přechodem pro

 0
vidíme, že pro
0
vidíme, že pro


 dostatečně malá je f(y) > f(a) pro
dostatečně malá je f(y) > f(a) pro  > 0 a f(y) < f(a) pro
> 0 a f(y) < f(a) pro  < 0. To je ve sporu s tím, že f má v bodě
a lokální extrém vzhledem k M.
< 0. To je ve sporu s tím, že f má v bodě
a lokální extrém vzhledem k M.
Nyní vyšetřeme
obecný případ, kdy
funkce gk
nejsou afinní. Pak bod y
sestrojený v předchozí
části
důkazu již
nemusí být prvkem množiny M, proto místo tohoto bodu
musíme uvažovat
jiný bod. Geometricky je jeho nalezení naznačeno na
obrázku 9.1
.
Označme v1,…,vn−m bázi prostoru Lin{g 1(a),…,g
1(a),…,g m(a)}
m(a)} a
uvažujme systém rovnic
a
uvažujme systém rovnic
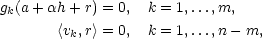
|
(9.4) |
kde r 
 n. Pak jsou vzhledem
k nezávislosti
vektorů g
n. Pak jsou vzhledem
k nezávislosti
vektorů g k(a) a výběru vektorů
vk splněny předpoklady Věty 8.3 a systém
rovnic (9.4) určuje
implicitně v okolí
bodu [
k(a) a výběru vektorů
vk splněny předpoklady Věty 8.3 a systém
rovnic (9.4) určuje
implicitně v okolí
bodu [ ,r] =
[0,0]
,r] =
[0,0] 


 n
funkci r = r(
n
funkci r = r( ) :
) : 

 n. Podle
Věty 8.3 pro její
derivaci podle
n. Podle
Věty 8.3 pro její
derivaci podle  dostáváme r
dostáváme r (
( )
)
 =0 = 0, což podle l’Hospitalova
pravidla znamená, že
=0 = 0, což podle l’Hospitalova
pravidla znamená, že
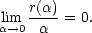
|
(9.5) |
Nyní položme y = a +  h +
r(
h +
r( ).
Podobně jako v první
části
důkazu platí
).
Podobně jako v první
části
důkazu platí
| f(y) |
= f(a) + 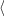 f f (a), (a), h + r( h + r( ) )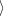 + +  ( ( h) = h) = |
|
|
|
= f(a) +  ![[ r(α) τ(αh)] 〈f′(a),h〉+ 〈f′(a),----〉+ ----- α α](diferencialni-pocet948x.png) |
|
|
a stejnou úvahou jako
výše v libovolném
okolí bodu a najdeme y,ỹ  M
taková, že f(y) < f(a) i f(y) > f(a) – spor.
□
M
taková, že f(y) < f(a) i f(y) > f(a) – spor.
□
Věta 9.1 říká, že v případě diferencovatelných
funkcí f
a gk
lokální extrém vzhledem k množině M může nastat pouze ve
stacionárním bodě. O tom, zda ve stacionárním
bodě nastává, nebo nenastává lokální extrém, rozhodneme pomocí vlastností
matice druhých
derivací Lagrangeovy funkce L
 (x,
(x, ).
).
Věta 9.2. Nechť
funkce f a gk,
k =
1,…,m mají spojité
parciální derivace
druhého řádu v bodě
a,
který je stacionárním
bodem f na M, a  1,…,
1,…, m jsou
příslušné Lagrangeovy
multiplikátory, tj. L
m jsou
příslušné Lagrangeovy
multiplikátory, tj. L (a,
(a, ) =
0. Dále nechť
matice (9.2
)
má
pro x
= a
hodnost m. Jestliže pro
každé 0≠h
) =
0. Dále nechť
matice (9.2
)
má
pro x
= a
hodnost m. Jestliže pro
každé 0≠h  Lin{g
Lin{g 1(a),…,g
1(a),…,g m(a)}
m(a)} platí
platí
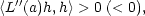
|
(9.6) |
má funkce
f v bodě
a ostré
lokální minimum (maximum)
vzhledem k M. Jestliže
existují h,h  Lin{g
Lin{g 1(a),…,g
1(a),…,g m(a)}
m(a)} taková, že
taková, že

|
(9.7) |
v bodě
a lokální extrém vzhledem k M
nenastává.
Důkaz.
Především si všimněme, že pro
x  M je f(x) = L(x), tj. x∗
M je f(x) = L(x), tj. x∗ M je lokálním extrémem f
vzhledem k M, právě když je lokálním
extrémem Lagrangeovy
funkce L.
Podobně jako v důkazu
Věty 9.1
můžeme body
y
M je lokálním extrémem f
vzhledem k M, právě když je lokálním
extrémem Lagrangeovy
funkce L.
Podobně jako v důkazu
Věty 9.1
můžeme body
y  M vyjádřit ve tvaru
y =
a +
M vyjádřit ve tvaru
y =
a +
 h + r(
h + r( ), kde h
), kde h
 Lin{g
Lin{g 1(a),…,g
1(a),…,g m(a)}
m(a)} a r :
a r : 

 n
splňuje (9.5
).
Pomocí Taylorova vzorce dostáváme
n
splňuje (9.5
).
Pomocí Taylorova vzorce dostáváme
| f(y) = |
L(y) = L(a) + 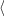 L L (a), (a), h +
r( h +
r( ) )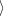 + +
 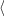 L L  (ã)( (ã)( h + r( h + r( ), ), |
|
|
( h + r( h + r( ) )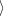 = = |
f(a) +  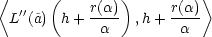 , , |
(9.8) |
kde ã
leží na úsečce spojující a a y (využili jsme faktu, že a je stacionární bod,
tj. L (a) = 0).
(a) = 0).
Předpokládejme,
že
platí (9.6), pak vzhledem ke spojitosti druhých
derivací funkce L
stejné nerovnosti
platí i pro ã
místo a, je-li


 dostatečně malé. Limitním přechodem pro
dostatečně malé. Limitním přechodem pro

 0
v (9.8) dostáváme pro
0
v (9.8) dostáváme pro


 dostatečně malé
dostatečně malé
![sgn[f(y)− f(a)] = sgn〈L′′(a)h,h〉,](diferencialni-pocet954x.png) tedy v bodě
a nastává lokální extrém f vzhledem k M, a to minimum, je-li
tedy v bodě
a nastává lokální extrém f vzhledem k M, a to minimum, je-li 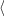 L
L
 (a)h,h
(a)h,h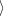 > 0, a maximum, platí-li
opačná nerovnost.
> 0, a maximum, platí-li
opačná nerovnost.
Nyní předpokládejme,
že
existují h,h  Lin{g
Lin{g 1(a),…,g
1(a),…,g m(a)}
m(a)} taková, že platí (9.7). Položme y1
= a
+
taková, že platí (9.7). Položme y1
= a
+  h + r(
h + r( ), y2
= a
+
), y2
= a
+  h + r(
h + r( ). Stejným způsobem
jako v předchozí
části
důkazu lze ukázat,
že
pro
). Stejným způsobem
jako v předchozí
části
důkazu lze ukázat,
že
pro 

 dostatečně malá platí
f(y1) > f(a) a f(y2) < f(a), tj. v bodě
a lokální extrém f vzhledem k M
nenastává. □
dostatečně malá platí
f(y1) > f(a) a f(y2) < f(a), tj. v bodě
a lokální extrém f vzhledem k M
nenastává. □
Nyní si
tvrzení posledních dvou
vět
shrňme do praktického návodu
hledání vázaných
extrémů funkcí
se spojitými
druhými derivacemi.
1.
Vytvoříme Lagrangeovu
funkci L(x, ) =
f(x) −∑ k=1m
) =
f(x) −∑ k=1m kgk(x).
kgk(x).
2. Určíme stacionární body
f vzhledem
k M, tj.
určíme x1,…,xn a
 1,…,
1,…, m jako
řešení systému n + m rovnic
m jako
řešení systému n + m rovnic
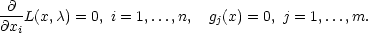 Nechť
a
Nechť
a  M je takto
vypočtený stacionární bod
f vzhledem
k M a
M je takto
vypočtený stacionární bod
f vzhledem
k M a  1,…,
1,…, m jsou
příslušející multiplikátory.
m jsou
příslušející multiplikátory.
3. Ze
systému m lineárních rovnic
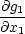 (a)h1 + ⋯ + (a)h1 + ⋯ + 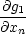 (a)hn
= 0 (a)hn
= 0 |
, |
|
|
| ⋮ |
|
|
|
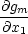 (a)h1 + ⋯ + (a)h1 + ⋯ + 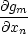 (a)hn
= 0 (a)hn
= 0 |
|
|
|
pro proměnné h1
,…,hn
vypočteme
m proměnných v závislosti na
n −
m zbývajících. Takto vypočtené vektory
h 
 n
jsou prvky tečného prostoru k M
v bodě
a,
n
jsou prvky tečného prostoru k M
v bodě
a,
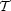 M(a) = Lin{g
M(a) = Lin{g 1(a),…,g
1(a),…,g m(a)}
m(a)} .
Tento výpočet je možný, neboť
podle předpokladu
má matice (9.2
)
hodnost m. Pro určitost předpokládejme,
že jsme
vypočetli h1,…,hm v z
ávislosti na hm+1,…,hn.
.
Tento výpočet je možný, neboť
podle předpokladu
má matice (9.2
)
hodnost m. Pro určitost předpokládejme,
že jsme
vypočetli h1,…,hm v z
ávislosti na hm+1,…,hn.
4. Určíme druhý
diferenciál Lagrangeovy funkce
vzhledem k proměnným x ve
stacionárním bodě
a
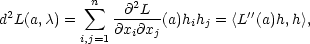 za
za  1,…,
1,…, m dosadíme příslušející multiplikátory a za
h1,…,hm vyjádření z předchozího bodu.
m dosadíme příslušející multiplikátory a za
h1,…,hm vyjádření z předchozího bodu.
5. Vyšetříme definitnost vzniklé kvadratické
formy n−m proměnných (je
to vlastně restrikce
kvadratické formy d2L(a, )
na tečný prostor
)
na tečný prostor
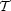 M(a)). Je-li tato forma
pozitivně (negativně)
definitní, nastává v bodě
a ostré
lokální minimum (maximum), a
je-li indefinitní, v bodě
a vázaný extrém nenastává.
M(a)). Je-li tato forma
pozitivně (negativně)
definitní, nastává v bodě
a ostré
lokální minimum (maximum), a
je-li indefinitní, v bodě
a vázaný extrém nenastává.
Příklad 9.1. i)
Najděte
lokální extrémy funkce u
= 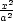 +
+ 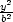 +
+ 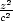 , a
> b > c, na
množině M : x2
+ y2
+ z2
= 1.
, a
> b > c, na
množině M : x2
+ y2
+ z2
= 1.
Řešení. Nejprve
sestavíme Lagrangeovu funkci úlohy a
určíme stacionární body.
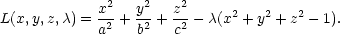 Derivováním a
přidáním vazebné
podmínky
dostáváme
Derivováním a
přidáním vazebné
podmínky
dostáváme
| Lx
= |
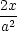 − 2 − 2 x = 0 ⇒ x x = 0 ⇒ x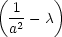 = 0, = 0, |
|
|
| Ly
= |
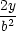 − 2 − 2 y = 0 ⇒ y y = 0 ⇒ y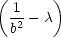 = 0, = 0, |
|
|
| Lz
= |
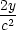 − 2 − 2 z = 0 ⇒ z z = 0 ⇒ z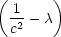 = 0, = 0, |
|
|
|
x2
+ y2
+ z2
= 1. |
|
|
Z prvních tří rovnic plyne, že vždy
dvě ze souřadnic
x,y,z musí být nulové
(neboť pouze jeden
z výrazů v závorkách může vždy být nulový). Dostáváme šestici stacionárních
bodů a příslušejících
multiplikátorů P1,2 = [ 1,0,0],
1,0,0], 1,2 =
1,2 = 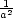 , P3,4 = [0,
, P3,4 = [0,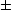 1,0],
1,0], 3,4 =
3,4 = 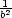 ,
P5,6 = [0,0,
,
P5,6 = [0,0,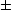 1],
1], 56
=
56
= 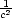 . Určíme
druhý diferenciál funkce
L (použijeme obvyklý
zápis
s dx,dy,dz místo h1,h2,h3)
. Určíme
druhý diferenciál funkce
L (použijeme obvyklý
zápis
s dx,dy,dz místo h1,h2,h3)
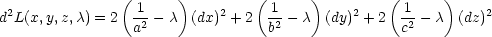 a diferencováním
vazebné podmínky dostáváme 2xdx + 2y dy + 2z dz = 0. Odsud plyne,
že
v bodech P1,2 je dx = 0, v bodech P3,4 je dy = 0 a v P5,6 je dz = 0. Využitím této skutečnosti
vyšetřeme definitnost formy d2L na tečném prostoru v bodech P1−6 ke kouli x2
+ y2
+ z2
= 1.
a diferencováním
vazebné podmínky dostáváme 2xdx + 2y dy + 2z dz = 0. Odsud plyne,
že
v bodech P1,2 je dx = 0, v bodech P3,4 je dy = 0 a v P5,6 je dz = 0. Využitím této skutečnosti
vyšetřeme definitnost formy d2L na tečném prostoru v bodech P1−6 ke kouli x2
+ y2
+ z2
= 1.
| P1,2 : |
d2L = 2(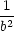 − −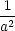 )(dy)2
+ 2( )(dy)2
+ 2( − −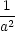 )(dz)2, )(dz)2, |
|
|
| P3,4 : |
d2L = 2(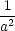 − −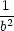 )(dx)2
+ 2( )(dx)2
+ 2(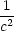 − −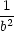 )(dz)2, )(dz)2, |
|
|
| P5,6 : |
d2L = 2(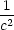 − −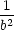 )(dx)2
+ 2( )(dx)2
+ 2(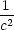 − −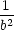 )(dz)2. )(dz)2. |
|
|
Protože a > b > c, je
kvadratická forma v bodech P1,2 pozitivně
definitní, v bodech
P5,6 negativně
definitní a v bodech P3,4 indefinitní. To
znamená, že v P1,2 je ostré
lokální minimum (rovno
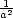 ), v P5,6 je ostré
lokální maximum
(rovno
), v P5,6 je ostré
lokální maximum
(rovno 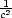 ) a v bodech P3,4 extrém nenastává.
) a v bodech P3,4 extrém nenastává.
ii)
Odvoďte vzorec pro vzdálenost bodu
x∗ = [x1∗,…,xn∗] od roviny a1x1
+ ⋯
+ anxn
= b
v prostoru 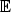 n.
n.
Řešení. Označme a = [a1,…,an], x = [x1,…,xn]. Pak můžeme úlohu zapsat ve vektorovém tvaru
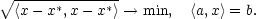 Je-li x bodem minima této úlohy, je
také bodem minima úlohy
Je-li x bodem minima této úlohy, je
také bodem minima úlohy
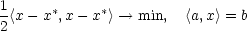 (tato úvaha
nám
usnadní derivování). Lagrangeova funkce
této úlohy je
(tato úvaha
nám
usnadní derivování). Lagrangeova funkce
této úlohy je
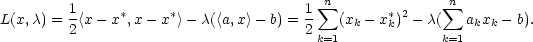 Derivováním
dostáváme (používáme pro stručnost
vektorový zápis)
Derivováním
dostáváme (používáme pro stručnost
vektorový zápis)
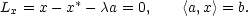 Z první
rovnice x = x∗
+
Z první
rovnice x = x∗
+  a a dosazením do
druhé rovnice
a a dosazením do
druhé rovnice 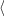 a,x∗
+
a,x∗
+  a
a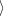 = b, odtud
= b, odtud
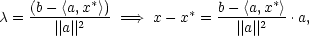 tedy
tedy
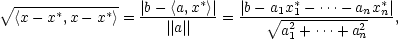 což
je vzorec dobře známý z lineární algebry.
což
je vzorec dobře známý z lineární algebry.
iii)
Určete obsah elipsy, která vznikne
při řezu elipsoidu 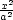 +
+ 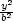 +
+ 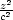 = 1 rovinou Ax
+ By
+ Cz
= 0 (obsah
elipsy je P = ppq, kde
p,q jsou
délky
poloos elipsy).
= 1 rovinou Ax
+ By
+ Cz
= 0 (obsah
elipsy je P = ppq, kde
p,q jsou
délky
poloos elipsy).
Řešení. K určení obsahu elipsy
potřebujeme určit délky
jejích poloos. To jsou
vzdálenosti bodů
ležících zároveň
na elipsoidu i v řezné rovině,
které mají nejmenší, resp. největší vzdálenost od počátku. Vzdálenost bodu [x,y,z] od počátku je dána vztahem
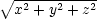 . Místo této funkce budeme hledat
extrémy funkce u
= x2
+ y2
+ z2,
která se snáze derivuje, a
vypočtený výsledek odmocníme. Řešíme tedy úlohu
. Místo této funkce budeme hledat
extrémy funkce u
= x2
+ y2
+ z2,
která se snáze derivuje, a
vypočtený výsledek odmocníme. Řešíme tedy úlohu
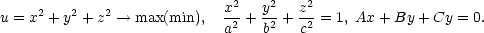 Lagrangeova funkce úlohy je
L(x,y,z,
Lagrangeova funkce úlohy je
L(x,y,z, ,
,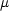 ) = x2 + y2
+ z2
−
) = x2 + y2
+ z2
− (
(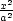 +
+  +
+ 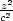 − 1) −
− 1) −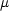 (Ax + By + Cy). Jejím derivováním a
připojením
vazebných podmínek
dostáváme systém rovnic
Vynásobíme-li
první rovnici x, druhou
y,
třetí z a sečteme je, pak
využitím vazebných
podmínek dostáváme rovnost
x2 + y2
+ z2
=
(Ax + By + Cy). Jejím derivováním a
připojením
vazebných podmínek
dostáváme systém rovnic
Vynásobíme-li
první rovnici x, druhou
y,
třetí z a sečteme je, pak
využitím vazebných
podmínek dostáváme rovnost
x2 + y2
+ z2
=  , tedy umax
=
, tedy umax
=  max a
umin =
max a
umin =  min.
Vyjádříme-li z prvních tří rovnic x,y,z
a dosadíme do rovnice
roviny, obdržíme rovnici
min.
Vyjádříme-li z prvních tří rovnic x,y,z
a dosadíme do rovnice
roviny, obdržíme rovnici
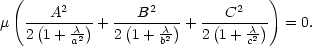 Protože
Protože 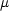 ≠0 (jinak
x =
y =
z = 0
a tento bod neleží na elipsoidu), z této rovnice
vynásobení
m jmenovateli zlomků
dostáváme
≠0 (jinak
x =
y =
z = 0
a tento bod neleží na elipsoidu), z této rovnice
vynásobení
m jmenovateli zlomků
dostáváme
Tuto rovnici
můžeme
přepsat do tvaru kvadratické rovnice
 2
+ K1
2
+ K1 + K2, kde
+ K2, kde
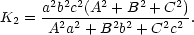 Koeficient K1
můžeme také
vyjádřit
explicitně, jeho hodnota však
není podstatná,
neboť rovnici nemusíme řešit.
Nepotřebujeme totiž
znát kořeny rovnice
Koeficient K1
můžeme také
vyjádřit
explicitně, jeho hodnota však
není podstatná,
neboť rovnici nemusíme řešit.
Nepotřebujeme totiž
znát kořeny rovnice  1,2,
nýbrž pouze jejich součin
1,2,
nýbrž pouze jejich součin  1
1 2 – ve
skutečnosti nepotřebujeme
znát délky poloos,
stačí nám znát jejich
součin. Tento součin je
roven absolutnímu členu
K2 v kvadratické
rovnici. Protože jsme hledali
extrémy funkce
x2 + y2
+ z2
místo funkce
2 – ve
skutečnosti nepotřebujeme
znát délky poloos,
stačí nám znát jejich
součin. Tento součin je
roven absolutnímu členu
K2 v kvadratické
rovnici. Protože jsme hledali
extrémy funkce
x2 + y2
+ z2
místo funkce
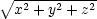 , je hledaná
plocha elipsy
, je hledaná
plocha elipsy
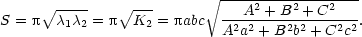
9.2 Vázané extrémy a nerovnosti
V tomto odstavci si ukážeme, jak lze v některých
speciálních (ale poměrně často se vyskytujících)
případech hledat
vázané extrémy, aniž
by bylo nutné
použít aparát
Lagrangeových multiplikátorů. I když
je tento postup poněkud vzdálený od metod
diferenciálního počtu,
uvádíme jej zde pro jeho výbornou praktickou použitelnost.
Čtenáři
doporučujeme všechny
úlohy
tohoto odstavce vyřešit pro
srovnání také metodou Lagrangeových multiplikátorů.
Nejprve
připomeňme pojem
kvadratického, aritmetického,
geometrického a harmonického
průměru n-tice čísel.
Nechť x1
,…,xn
jsou kladná reálná čísla,
označme
 n(x1,x2,…,xn) = n(x1,x2,…,xn) = |
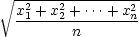 , , |
|
|
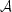 n(x1,x2,…,xn) = n(x1,x2,…,xn) = |
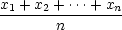 , , |
|
|
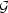 n(x1,x2,…,xn) = n(x1,x2,…,xn) = |
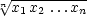 , , |
|
|
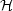 n(x1,x2,…,xn) = n(x1,x2,…,xn) = |
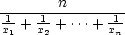 . . |
|
|
Věta 9.3. Nechť
x =
[x1,…,xn] je n-tice kladných čísel. Platí
nerovnosti
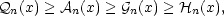 přičemž rovnosti
nastávají, právě když x1
= x2
= ⋯
= xn.
přičemž rovnosti
nastávají, právě když x1
= x2
= ⋯
= xn.
Důkaz.
Viz skriptum [H-K-S].
□
Kromě nerovností
mezi průměry je
účinným nástrojem i tzv.
Cauchyova nerovnost.
Věta 9.4. Pro
libovolné dvě n-tice
reálných čísel x = (x1,…,xn),y = (y1,…,yn) platí
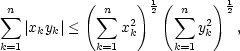 přičemž rovnost nastane,
právě když existuje reálné t takové, že yk
= txk, k =
1,…,n, tj. právě když vektory
x a
y jsou
lineárně závislé.
přičemž rovnost nastane,
právě když existuje reálné t takové, že yk
= txk, k =
1,…,n, tj. právě když vektory
x a
y jsou
lineárně závislé.
Příklad 9.2. i)
Mezi všemi trojúhelníky s konstantním
obvodem o určete ten,
který má největší obsah.
Řešení. Vyjdeme z Heronova vzorce pro obsah trojúhelníka
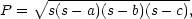 kde a,b,c jsou strany
trojúhelníka a s = (a+b+c)∕2 = o∕2 je tzv.
poloperimetr. Označíme-li
x =
s−a, y = s−b, z = s−c a uvážíme-li, že
najít
maximum funkce P
je totéž jako najít maximum funkce
P
= s−
kde a,b,c jsou strany
trojúhelníka a s = (a+b+c)∕2 = o∕2 je tzv.
poloperimetr. Označíme-li
x =
s−a, y = s−b, z = s−c a uvážíme-li, že
najít
maximum funkce P
je totéž jako najít maximum funkce
P
= s−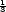 P
P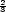 , můžeme úlohu formulovat
takto:
, můžeme úlohu formulovat
takto:
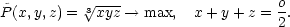 Využitím nerovnosti mezi
algebraickým a geometrickým průměrem dostáváme
Využitím nerovnosti mezi
algebraickým a geometrickým průměrem dostáváme
 přičemž rovnost
nastává, právě když x = y = z = o∕2. Máme tedy systém rovnic
přičemž rovnost
nastává, právě když x = y = z = o∕2. Máme tedy systém rovnic
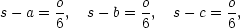 jehož
řešením je a = b = c = o∕3. Tedy mezi
všemi
trojúhelníky s daným obvodem
o má největší obsah
rovnostranný trojúhelník a tento
maximální obsah je Pmax
=
jehož
řešením je a = b = c = o∕3. Tedy mezi
všemi
trojúhelníky s daným obvodem
o má největší obsah
rovnostranný trojúhelník a tento
maximální obsah je Pmax
=  .
.
ii) Mezi
všemi
trojicemi kladných čísel x,y,z s konstantním součtem a
najděte ta, pro
která je součet převrácených hodnot
minimální.
Řešení. Z nerovnosti mezi harmonickým a
aritmetickým průměrem dostáváme
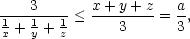 přičemž rovnost nastane,
právě když x = y = z = a∕3. Odtud
přičemž rovnost nastane,
právě když x = y = z = a∕3. Odtud  +
+  +
+
 ≥
≥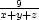 =
=  , tedy součet převrácených hodnot je
minimální, jsou-li
všechna tři čísla stejná
a rovna
, tedy součet převrácených hodnot je
minimální, jsou-li
všechna tři čísla stejná
a rovna 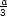 .
.
iii) Na elipsoidu
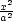 +
+ 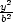 +
+ 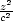 = 1 najděte bod v prvním oktantu
s vlastností, že objem
čtyřstěnu tvořeného
souřadnými stěnami a
tečnou rovinou
k elipsoidu
v tomto bodě je
minimální.
= 1 najděte bod v prvním oktantu
s vlastností, že objem
čtyřstěnu tvořeného
souřadnými stěnami a
tečnou rovinou
k elipsoidu
v tomto bodě je
minimální.
Řešení. Nejprve
připomeňme, že objem
čtyřstěnu vypočteme podle
vzorce V =  x0y0z0, kde
[x0,0,0],[0,y0,0],[0,0,z0] jsou průsečíky tečné roviny se
souřadnými osami
(sestrojíme-li trojboký
hranol se základnou
tvořenou trojúhelníkem s vrcholy [0,0,0], [x0,0,0], [0,y0,0] a výškou z0, jeho objem
je
x0y0z0, kde
[x0,0,0],[0,y0,0],[0,0,z0] jsou průsečíky tečné roviny se
souřadnými osami
(sestrojíme-li trojboký
hranol se základnou
tvořenou trojúhelníkem s vrcholy [0,0,0], [x0,0,0], [0,y0,0] a výškou z0, jeho objem
je 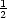 x0y0z0
a je trojnásobkem objemu
daného čtyřstěnu). Vyjádřením proměnné z z rovnice elipsoidu nebo pomocí derivace
implicitní funkce snadno
ověříme, že rovnice tečné roviny
k elipsoidu
v bodě [x,y,z] je
x0y0z0
a je trojnásobkem objemu
daného čtyřstěnu). Vyjádřením proměnné z z rovnice elipsoidu nebo pomocí derivace
implicitní funkce snadno
ověříme, že rovnice tečné roviny
k elipsoidu
v bodě [x,y,z] je
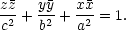
|
(9.9) |
Odtud
dostáváme, že úseky vyťaté tečnou rovinou na
souřadných osách jsou x0
= 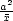 (položíme y = 0 = z v (9.9)),
z0 =
(položíme y = 0 = z v (9.9)),
z0 = 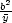 , z0
=
, z0
= 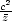 . Řešíme tedy úlohu
. Řešíme tedy úlohu
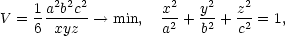 která
je, pokud jde o extremální bod,
ekvivalentní úloze
která
je, pokud jde o extremální bod,
ekvivalentní úloze
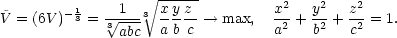 Z nerovnosti mezi kvadratickým a
geometrickým průměrem dostáváme, že Ṽ je
maximální, jestliže
Z nerovnosti mezi kvadratickým a
geometrickým průměrem dostáváme, že Ṽ je
maximální, jestliže 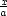 =
= 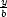 =
=  , což vzhledem
k vazebné podmínce nastane, když x =
, což vzhledem
k vazebné podmínce nastane, když x = 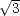 a, y =
a, y = 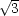 b, z =
b, z = 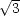 c, a pro tyto hodnoty dostáváme
minimální objem V
min =
c, a pro tyto hodnoty dostáváme
minimální objem V
min = 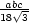 .
.
iv) Na elipsoidu
x2 + 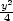 +
+ 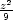 = 1 najděte bod, který
je nejblíže rovině
x +
y +
z =
2
= 1 najděte bod, který
je nejblíže rovině
x +
y +
z =
2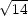 .
.
Řešení. Pro
vzdálenost bodu [x0,y0,z0] od roviny ax
+ by
+ cz
= d
platí
vzorec (viz
Příklad 9.1 ii))
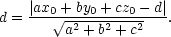 Protože elipsoid
leží pod rovinou
x +
y +
z =
2
Protože elipsoid
leží pod rovinou
x +
y +
z =
2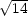 , budeme řešit úlohu
, budeme řešit úlohu
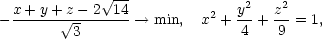
|
(9.10) |
která je (pokud jde
o bod, v němž je
dosaženo minima) ekvivalentní úloze
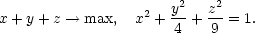 Tuto úlohu
vyřešíme
pomocí Cauchyovy nerovnosti. Platí
Tuto úlohu
vyřešíme
pomocí Cauchyovy nerovnosti. Platí
 přičemž rovnost
nastává, právě když jsou vektory (x,
přičemž rovnost
nastává, právě když jsou vektory (x,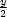 ,
,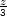 ), (1,2,3) lineárně závislé,
tj. existuje
t
), (1,2,3) lineárně závislé,
tj. existuje
t 
 takové, že x = t,
takové, že x = t, 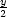 = 2t,
= 2t, 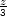 = 3t. Vezmeme-li v úvahu vazebnou
podmínku x2
+
= 3t. Vezmeme-li v úvahu vazebnou
podmínku x2
+ 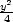 +
+ 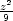 = 1, dostáváme t =
= 1, dostáváme t = 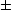
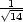 , tj. (hledaný
bod leží v I.
kvadrantu)
, tj. (hledaný
bod leží v I.
kvadrantu)
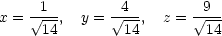 a dosazením do (9.10
)
dostáváme dmin
=
a dosazením do (9.10
)
dostáváme dmin
= 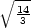 .
.
Cvičení 
9.1. Určete vázané extrémy funkce f
na množině určené rovnostmi:
|
a) f(x,y,z) = xy2z3, x + 2y + 3z = a, a,x,y,z > 0 |
|
b) f(x,y,z) = sinxsiny sinz, x + y + z = 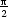 |
|
c) f(x,y,z) = xyz, x2
+ y2
+ z2
= 1,
x +
y +
z = 0 |
|
d) f(x,y,z) = xy + yz, x2
+ y2
= 2,
y +
z =
2, x,y,z > 0 |
|
e) f(x1,…,xn) = x12
+ ⋯
+ xn2, 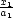 + ⋯ + + ⋯ + 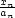 = 1, ai
> 0, i =
1,…,n = 1, ai
> 0, i =
1,…,n |
|
f) f(x1,…,xn) = 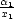 +…+ +…+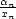 , , 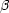 1x1
+ ⋯
+ 1x1
+ ⋯
+ 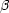 nxn
= 1, nxn
= 1,
 i, i,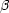 i,xi
> 0, i =
1,…,n i,xi
> 0, i =
1,…,n |
|
g) f(x1,…,xn) = x1 1…xn 1…xn n,
x1 + ⋯ + xn
= 1, n,
x1 + ⋯ + xn
= 1,
 i
> 0, i =
1,…,n i
> 0, i =
1,…,n |
9.3. Řešte
extremální úlohy:
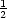

 x
x
 2
2
 min,
min, 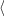 u,x
u,x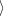 =
=
 ,
, 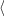 v,x
v,x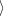 =
= 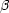 , x,u,v
, x,u,v 
 n,
n,
 ,
,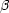

 ;
;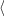 Ax,x
Ax,x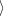
 min,
min, 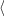 uk,x
uk,x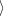 =
=  k, k =
1,…,n − 1, x,uk
k, k =
1,…,n − 1, x,uk

 n,
n,
 k
k

 ,
,
dim{Lin{u1,…,un−1}} = n − 1.
∗
Všechny
dobré zásady jsou již
napsány.
Nyní ještě zbývá je uskutečnit.
(B. Pascal)
∗
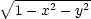 a
funkci f(x,y,
a
funkci f(x,y,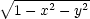 ) vyšetřujeme na množině M :
x2 + y2
≤ 1, x,y ≥
0, tj. najdeme
stacionární body uvnitř
M
a vyšetříme funkci na hranici množiny M. Provést toto na
části hranice
tvořené čtvrtkružnicí znamená
vyjádřit y =
) vyšetřujeme na množině M :
x2 + y2
≤ 1, x,y ≥
0, tj. najdeme
stacionární body uvnitř
M
a vyšetříme funkci na hranici množiny M. Provést toto na
části hranice
tvořené čtvrtkružnicí znamená
vyjádřit y = 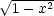 a dosadit
do f,
tj. vyšetřovat funkci f(x,
a dosadit
do f,
tj. vyšetřovat funkci f(x,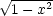 ,0) pro x
,0) pro x  [0,1].
[0,1].




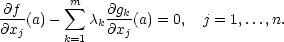
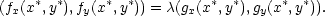

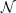
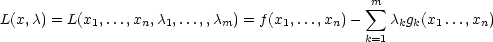
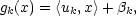

 h
h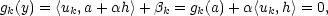
![[ ] ′ ′ τ(αh) f(y) = f(a)+ α〈f(a),h〉+ τ(αh) = f(a)+ α 〈f (a),h 〉+ α ,](diferencialni-pocet942x.png)


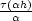
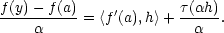





![[ r(α) τ(αh)] 〈f′(a),h〉+ 〈f′(a),----〉+ ----- α α](diferencialni-pocet948x.png)

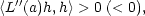



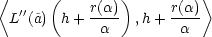
![sgn[f(y)− f(a)] = sgn〈L′′(a)h,h〉,](diferencialni-pocet954x.png)