D. Antropometrie, somatometrie
D01 Relativní hmotnost částí lidského těla
Při biomechanické analýze některých sportů potřebujeme znát hmotnosti hlavních částí lidského těla. Měřením těchto hmotností různými metodami se zabývala řada autorů, v [35] je přehled jejich výsledků v procentech hmotnosti celého těla. Vážené průměry s ohledem na počet změřených osob jsou v následující tabulce:
| část těla | muži | ženy |
|---|---|---|
| hlava | 7,14 | 7,14 |
| trup+hlava | +45,59 = 52,73 | 52,64 |
| paže | 2 × 2,856 = 5,712 | 2 × 2,825 = 5,65 |
| předloktí | 2 × 1,733 = 3,466 | 2 × 1,653 = 3,305 |
| ruka | 2 × 0,655 = 1,310 | 2 × 0,502 = 1,004 |
| stehno | 2 × 12,556 = 25,112 | 2 × 12,26 = 24,52 |
| bérec | 2 × 4,476 = 8,952 | 2 × 5,059 = 10,118 |
| noha | 2 × 1,437 = 2,974 | 2 × 1,256 = 2,513 |
| S = 100,16 % | S = 99,97 % |
Těmito procenty počítáme hmotnost částí těla z hmotnosti celého těla. Jestliže současně s hmotností části těla byla měřena nejen hmotnost celého těla M, ale i jeho výška H, můžeme získat (programem pro lineární aproximaci funkce dvou nezávislých proměnných z=f(x,y)) C07 rovnice pro dvojnásobnou regresi:
V uvedené literatuře jsou tyto rovnice:
| hlava | m1 = 0,0171 × M + 0,0143 × H + 1,296 |
| trup | m2 = 0,5072 × M – 0,07574 × H + 7,8974 |
| paže | m3 = 0,0312 × M – 0,0027 × H + 0,25 |
| předloktí | m4 = 0,01445 × M – 0,00114 × H + 0,3185 |
| ruka | m5 = 0,0036 × M + 0,00175 × H – 0,1165 |
| stehno | m6 = 0,1463 × M + 0,0137 × H – 2,649 |
| bérec | m7 = 0,03616 × M + 0,0121 × H – 1,592 |
| noha | m8 = 0,0077 × M + 0,0073 × H – 0,829 |
| horní končetina | mh = 0,04925 × M – 0,00209 × H + 0,452 |
| dolní končetina | md = 0,19016 × M + 0,0331 × H – 5,067 |
Má-li součinitel b u tělesné výšky H kladné znaménko, pak hmotnost této části těla roste s rostoucí výškou (hlava, ruka, všechny části dolní končetiny), při záporném znaménku hmotnost klesá s rostoucí tělesnou výškou (trup, nadloktí, předloktí a celá horní končetina).
muž s M = 75 kg a H = 175 cm bude mít
| hmotnost hlavy | m1 = 5,081 kg | 6,77 % |
| hmotnost trupu | m2 = 32,6829 kg | 43,58 % |
| hmotnost paží | mh = 7,56 kg | 10,06 % |
| hmotnost paží a nohou | md = 29,975 kg | 39,97 % |
| celkem | 75,2689 kg | 100,38 % |
Literatura
- Hay J. G.: The biomechanics of sports techniques. 1985, Prentice Hall Intrnat. Inc., Englewood Cliffs, New Jersey, str. 157
- Zaciorskij V. M. – Aruin A. S. – Selujanov V. N.: Biomechanika dvigatělnogo apparata čeloveka. 1981, FiS, Moskva, str. 29, 38–39, 118
- Donskoj D. D. – Zaciorskij V. M.: Biomechanika. 1979, FiS, Moskva, str. 61
D02 Těžiště a momenty setrvačnosti lidského těla
V biomechanice sportů je poloha těžiště sportovce významná v řadě sportů, např. skocích, gymnastice a akrobacii apod. Protože části těla mohou měnit svou relativní polohu ve velkém rozsahu, může se tak měnit i poloha těžiště vůči tělu. S rozvojem snímací a výpočetní techniky již není problém analyzovat 3D model pohybu [39].
Stanovíme ji pomocí jejích souřadnic v prostoru:
kde xi, yi, zi jsou prostorové souřadnice těžiště částí těla
mi … hmotnosti částí těla
pi … procentní hmotnosti částí těla (předchozí kapitola)
Pozn.: zpravidla je zobrazení sportovce rovinné (film, fotografie, videozáznam) a počítáme jen xT, yT.
Chyby stanovení souřadnic těžiště jsou způsobeny odchylkami procentního rozdělení hmotností u daného sportovce od uvedených středních hodnot, nepřesností zobrazení a stanovení polohy těžišť jednotlivých částí těla.
Při rotačních pohybech (překotech a vrutech) je setrvačnost těla jako odpor proti změně rotací závislá na momentu setrvačnosti, nikoliv na hmotě těla. Momenty setrvačnosti počítáme vzorci
kde xi, yi … vzdálenosti těžiště od osy y,x
mi … hmotnosti části těla
pi … procentní hmotnosti části těla
s … měřítko zobrazení (např. 1:20 = 0.05)
k = 100 · s2 / M … konstanta, vyjadřující vliv měřítka zobrazení s a hmotnosti celého těla M
Moment setrvačnosti k ose z, (procházející kolmo na osy x,y jejich průsečíkem) je
Poloměr setrvačnosti je odmocnina momentu setrvačnosti k těžištní ose, děleného hmotností těla. Je to míra setrvačnosti těla při rotačních zrychleních.
Následující program provede všechny potřebné výpočty (sumace) jestliže vkládáme podle obrazovky žádané souřadnice x, y, nakonec hmotnost těla (kg) a měřítko zobrazení jako desetinný zlomek.
Literatura
- Hay James G.: The Biomechanics of Sports Technique. 1985, 3. vyd.Prentice-Hall International Inc., Englewood Cliffs, N. J., USA
- Zvonař, Martin; Sebera, Martin. Simi motion 3D biomechanická analýza. Studia sportiva, Brno, FSpS MU Brno. ISSN 1802-7679, 2007, vol. 2/1, no. 1, 116 s.
INPUT "jméno,datum="; n$, d$
PRINT "hlava ";: p = 7.14: GOSUB g
PRINT "trup ";: p = 45.59: GOSUB g
PRINT "pravá paže ";: p = 2.856: GOSUB g
PRINT "levá paže ";: GOSUB g
PRINT "pravé předloktí ";: p = 1.733: GOSUB g
PRINT "levé předloktí ";: GOSUB g
PRINT "pravá ruka ";: p =.655: GOSUB g
PRINT "levá ruka ";: GOSUB g
PRINT "pravé stehno ";: p = 12.556: GOSUB g
PRINT "levé stehno ";: GOSUB g
PRINT "pravý bérec ";: p = 4.476: GOSUB g
PRINT "levý bérec ";: GOSUB g
PRINT "pravá noha ";: p = 1.437: GOSUB g
PRINT "levá noha ";: GOSUB g
xt = sx / 100: yt = sy / 100
PRINT "souřadnice těžiště x,y "; xt, yt
INPUT "hmotnost těla "; m
INPUT "měřítko délek "; s
k = 1E+08*s*s/ m
ix = ky / k: iy = kx / k
PRINT "Ix,Iy "; ix, iy
i = ix + iy
it = i – 100 * (xt * xt + yt * yt) / k
PRINT "It="; it
r = SQR(it / m)
PRINT "poloměr setrvačnosti "; r
END
g:
INPUT "xt,yt "; x, y
sx = sx + p * x: kx = kx + p * x * x
sy = sy + p * y: ky = ky + p * y * y
RETURN
v knize J.G.Haye je na str. 136 obrázek skokana do dálky. Odměříme-li souřadnice těžišť částí těla, dostaneme
| část těla | x | y |
|---|---|---|
| hlava | 3 | 23 |
| trup | 3 | 3 |
| pravá paže | 10 | 17.5 |
| levá paže | -2.5 | 18 |
| pravé předloktí | 12 | 25 |
| levé předloktí | -12 | 26.5 |
| pravá ruka | 16 | 36 |
| levá ruka | -21 | 36 |
| pravé stehno | -11 | -11.5 |
| levé stehno | 4 | -20.5 |
| pravý bérec | -31,5 | -9.5 |
| levý bérec | 12.5 | -30 |
| pravá noha | -49 | -10.5 |
| levá noha | 22 | -20.5 |
Protože počátek souřadnic je v průsečíku os x,z, mají být tyto souřadnice 0,0. Vidíme, že chyba je malá.
Hmotnost těla: 75
Měřítko délek 0.0543
Ix,Iy 5.623 3.406
It 9.028
Poloměr setrv. 0.347
D03 Starší antropometrické indexy
Chceme-li popsat tělesný typ sportovce bez měření mnoha parametrů a výpočtu somatotypu Heathové a Cartera, můžeme někdy použít starší antropometrické indexy, navržené slavnými antropology. Ty také umožňují srovnání dřívějších sportovců, u nichž jsou tyto indexy známé, s dnešními.
Starší indexy vycházejí z hmotnosti M (kg), tělesné výšky H (cm, dm), obvodu hrudníku O (cm) a vitální kapacity VK (litrů).
| Bouchardův index | BC = M / H | (kg/dm) |
| Brockův index | BR = M / (H-100) | (kg/cm) |
| Brugschův index | BG = OH. 100 / H | (bez rozměrů) |
| Erismannův index | E = OH – H / 2 | (cm) |
| Pignet-Pinnierův index | PP = M + OH – H | |
| Šulcův typový součinitel | T = M / H2,5.105 | (kg/cm2,5) |
| povrch těla podle Du-Bois Reymonda | PO = 7,148.M0,425.H0,725 | |
| vitální kapacita na 1 m2 povrchu těla | V = VK / PO |
Povrch těla lze určit nomogramem, nahrazujícím uvedený vzorec
Nomogram najdeme v knihách:
Literatura
- Drastich L.: Tělověda. 1948, Praha-Brno, Komenium, str. 151
- Sobolová V. – Zelenka V.: Fysiologie tělesných cvičení a sportu 1973, Praha, Olympia, obr. 37
Normy pro antropometrické indexy:
| muži | ženy | |||||||
|---|---|---|---|---|---|---|---|---|
| index | pyknik | atlet | leptosom | průměr | pyknička | atletka | leptosomka | průměr |
| bc | 4.05 | 4.14 | 3.96 | 4.08 | 3.93 | 3.8 | 3.5 | 3.74 |
| br | 1.1 | 1 | 0.8 | 1 | ||||
| bg | 55.7 | 54.8 | 53 | 54.6 | 53.8 | 53 | 51 | 52.6 |
| e | 9.9 | 7.7 | 5.3 | 8 | 6 | 5.2 | 1.6 | 4.3 |
| pp | -6.2 | -6.2 | -12.9 | 9 | -10.5 | -14.4 | -23 | -16 |
| vk/po | 2.78 | 2.77 | 2.7 | 2.74 | 1.9 | 2.12 | 2.13 | 2.07 |
Program pro výpočet indexů:
INPUT "hmotnost (kg), výška (cm)="; m,h
INPUT "obvod hrudníku (cm), vitální kapacita (litrů) ="; o,v
bc=10*m/h: PRINT "Bouchardův index=";bc
br=m/(h-100): PRINT "Brocův index=";br
t=m/h^2.5*10e05:PRINT "Šolcův typový součinitel=";t
po=7.148E-03*m^.425*h^.725:PRINT "povrch těla=";po
v=vk/po:PRINT "vitální kapacita na 1 m^2=";v
if o=0 THEN GOTO k
bg=o*100/h:PRINT "Brugschův index=";bg
e=o-h/2:PRINT"Erismannův index=";e
pp=m+o-h:PRINT "Pignet-Pinnierův index=";pp
k:
END
muž s m=75 kg, h=175 cm, o=100 cm, vk=7 litrů:
bc= 4.29, br=1, bg= 57.1, e=12.5, pp= 0, t= 18.51, po= 1.8935 m2
vk/po= 3.697 litrů/m2
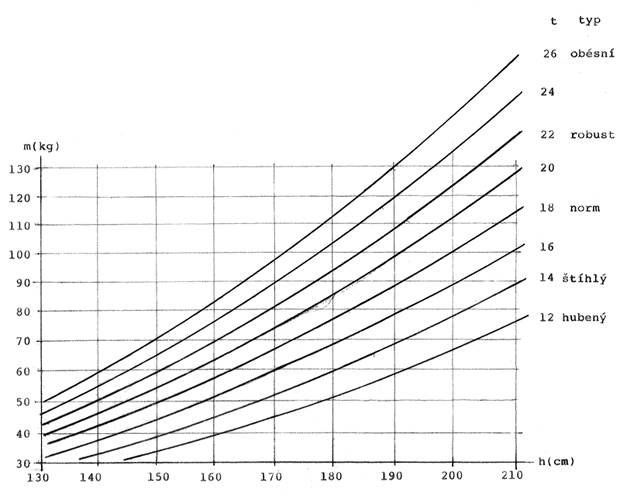
D04 Typový součinitel podle Šolce a Lochmana
Není-li možné změřit všechna data, potřebná k výpočtu složek somatotypu, nebo chceme-li jednoduše hodnotit typ lidského těla, můžeme použít typový součinitel, založený jen na hmotnosti m a výšce těla h pomocí vzorce
| Příklady: | m(kg) | h(m) | t | typ |
|---|---|---|---|---|
| gymnastka | 42 | 1,592 | 14,3 | velmi štíhlá |
| gymnasta | 51 | 1,626 | 15,4 | štíhlý |
| basketbalista | 75,5 | 1,885 | 16,8 | štíhlý |
| volejbalistka | 73,3 | 1,834 | 16,1 | štíhlá |
| fotbalista | 71 | 1,735 | 17,9 | průměrný |
| vzpěrač | 100 | 1,80 | 23 | velmi robustní |
| nesportovec | 130 | 1,80 | 29,9 | velmi obézní |
Následující nomogram usnadňuje určení typového součinitele a srovnávání různých skupin sportovců podobně, jako somatotyp.
Literatura
- Šolc I. – Lochman J.: Kvantitativní vztahy v typologii člověka. Vesmír 61, 1982, č. 3, str. 71–74
cls: screen 10: key off
pset(0,0)
draw "d320;r640"
FOR h=130 TO 210 STEP 10
y=320-(h-130)*4
line(0,y)-(5,y)
NEXT h
FOR m=30 TO 130 STEP 10
x=(m-30)*6
line(x,320)-(x,325)
NEXT m
FOR k=13 to 25 STEP 2: pset(0,320)
FOR m=30 TO 130 STEP 30
m=(m*100000/k)^.4
line-((m-30)*6,320-(h,130)*4)
NEXT m: next k
END
D05 Výpočet složek somatotypu podle Heathové a Cartera
V roce 1967 publikovali B. H. Heathová a J. E. Carter metodu, jak stanovit složky somatotypu.
Musíme změřit tyto parametry:
tělesnou výšku v cm, tloušťky tří kožních řas v mm, šířky epikondylů kosti pažní a stehenní a obvody bicepsu paže a lýtka v cm a tělesnou hmotnost. Pak můžeme vypočítat složky somatotypu následujícím programem.
Literatura
- Heath B. H. – Carter J. E.: A modified somatotype method. Amer. J. Phys. Anthrop. 27, 1967, p. 57–74
- Kopřiva J. – Čechovský K.: Determination of Heath-Carter somatotype and somatotype dispersion index using a computer. Anthropologie 28, 1990, p. 31–33
INPUT "součet tří kožních řas(mm)=";s
IF s<31.3 mm THEN en=.125*s-.625 ELSE en=24.447*s/(195.207+s)
INPUT "těles.výška(cm)=";h
INPUT "šířka pažního epikondylu=";u
INPUT "šířka stehenního epikondylu=";f
INPUT "obvod bicepsu paže=";b
INPUT "obvod lýtka=";c
n1=(h-78.7)/3.81132
n2=(u-2.87)/.14566
n3=(f-4.09)/.207736
n4=(b-13.1)/.664151
n5=(c-15.3)/.771358
me=(n2+n3+n4+n5-4*n1)/8+4
INPUT "těles.hmotnost (kg)=";m
i=h/m^(1/3)
ek=.709671*i-27.434
PRINT "somatotyp: en-me-ek ";sing "##.##";en,me,ek
END
s=35 mm, h=175 cm, šířka epik.p= 6 cm, šířka epik.s = 10 cm,
obvod bicepsu paže = 29 cm, obvod lýtka = 40 cm,
těles.hmotnost = 73 kg.
en – me – ek = 3.44 4.60 2.28
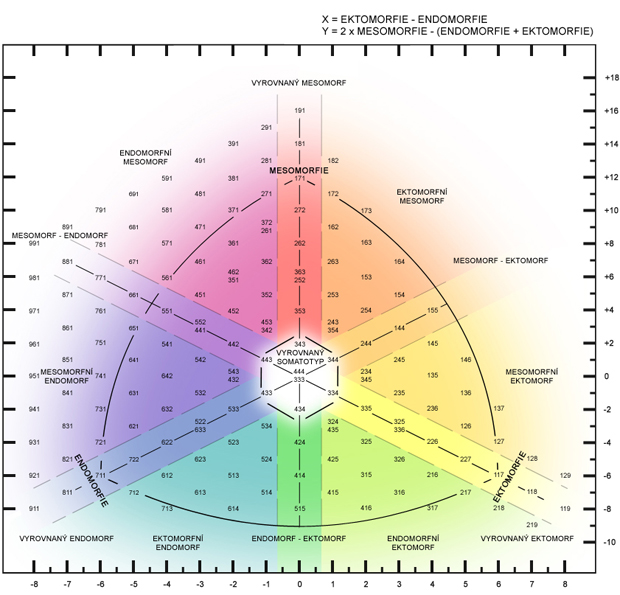
D06 Grafické vyjádření somatotypu Heathové a Cartera
Tři složky somatotypu Heathové a Cartera (endomorfie, mesomorfie a ektomorfie) lze zobrazit v rovinném grafu pomocí transformačních rovnic:
Pak můžeme somatotyp vyjádřit bodem v souřadnicích x,y uvnitř sférického trojúhelníka, jehož středy křivosti leží v jeho vrcholech. Kreslení několika somatotypů různě barevnými body provede následující program.
screen 9: cls: key off
locate 20,22: PRINT "endo"
locate 1,50: PRINT "meso"
locate 20,76: PRINT "ekto"
circle(400,10),400,,4.189,5.236
circle(200,265),400,,0,1.047
circle(600,262),400,,2.094,3.1416: b=0
locate 1,1
a:
INPUT "en,me,ec=";en,me,ec: b=b+1
IF b=1 THEN PRINT "modrý"
IF b=2 THEN PRINT "zelený"
IF b=3 THEN PRINT "tyrkys"
IF b=4 THEN PRINT "červený"
IF b=5 THEN PRINT "purpur"
IF b=6 THEN PRINT "světle červený"
IF b=7 THEN PRINT "světlý purpur"
IF b=8 THEN PRINT "šedý"
IF b=9 THEN PRINT "světle modrý"
x=(ec-en)*.866
y=me-(en+ec)*.5
circle(400+x*38.5,178-y*28),3,b
GOTO a
END
po spuštění programu se nakreslí sférický trojúhelník, vložíme vyžádané složky a somatotyp se zakreslí barevným kroužkem. Zapíšeme si barvu ke jménu osoby a vkládáme další somatotyp. Skončíme kombinací CTRL+C.
D07 SDI – index rozptylu somatotypu
Používáme-li somatotyp podle Heathové a Cartera, můžeme někdy potřebovat popsat určitou skupinu sportovců
- somatotypy jednotlivců
- průměrným somatotypem celé skupiny
- nějakým měřítkem rozptylu těchto somatotypů.
Pro toto použití navrhli Ross a Wilson SDI, tj. index rozptylu somatotypů, který lze vypočítat následujícím programem.
Literatura
- Ross W. D. – Wilson B. D.: A Somatotype Dispersion Index. Research Quarterly, 44, 1973, str. 372–374.
DATA en1,me1,ec1,en2,me2,ec2,… enp,mep,ecp
INPUT "počet osob ";p: print
DIM n(p),m(p),k(p),x(p),y(p)
FOR i=1 TO p
READ n(i),m(i),k(i)
a=a+n(i):b=b+m(i):c=c+k(i)
x(i)=k(i)-n(i)
y(i)=2*m(i)-k(i)-n(i)
NEXT i
a=a/p:b=b/p:c=c/p
PRINT "průměrný somatotyp =";a,b,c: PRINT
x=c-a:y=2*b-a-c
d=0:for i=1 to p
d=d+sqr((3*x(i)-x)^2+(y(i)-y)^2)
NEXT i: d=d/p
PRINT "SDI=";d
END
som1 = 3 – 5 – 2
som2 = 2 – 6 – 3
som3 = 2 – 5 – 4
som4 = 3 – 4 – 4
som5 = 3 – 5 – 4
průměrný somatotyp 2,6 – 5,0 – 3,4
SDI 2,49
D08 Celkové procento tělesného tuku z tloušťky 4 kožních řas
V literatuře [46] jsou údaje a poměrně složité vzorce pro výpočet celkového procenta tělesného tuku ze 4 kožních řas
s1 uprostřed nadloktí nad m.triceps brachii
s2 na zádech na dolním konci lopatky
s3 na hrudní axilární čáře ve výšce 7. žebra
s4 na břiše v horní části mezi pupkem a crista illiaca
Ze součtu všech 4 řas s = s1 + s2 + s3 + s4
můžeme počítat velmi jednoduchým vzorcem procento tuku
|
u mužů |
t % = 11,8686 · ln(s) – 28,413 |
r=0,9999920 |
|
u žen |
t % = 14,0123 · ln(s) – 32,774 |
r=0,999994 |
Literatura
- Mohr M.: Methods of Epidemiological Nutritional Status Assesment of Adults. In: Methods of Functional Anthropology. Proc. Symposium, 5–8. 9. 1977 in Prague. Prague, 1979, str. 139–144
Fakulta sportovních studií, Masarykova univerzita |
Návrat na úvodní stránku webu, přístupnost |
| Servisní středisko pro e-learning na MU
| Fakulta informatiky Masarykovy univerzity, 2011
Technické řešení této výukové pomůcky je spolufinancováno Evropským sociálním fondem a státním rozpočtem České republiky.