C. Matematika
část C06–C10
C06 Aproximace empirické závislosti 16 funkcemi
Je-li dána empirická závislost dvou veličin řadou dvojic souřadnic x, y nebo křivkou y = f(x), na které lze tyto souřadnice stanovit, může být výhodné nahradit tyto formy dat aproximační funkcí typu
např. funkcí y = a + b · x, nebo některou funkcí, kterou lze vhodnou transformací (linearizací) na tuto funkci převést:
apod.
Následující program zpracuje data ve formě dvojic x, y výpočtem a, b pro 16 funkcí a k tomu součinitelů nelineární korelace, pomocí nichž můžeme vybrat funkci, nejlépe aproximující vstupní data. Přirozeně nemůže dvouparametrová funkce dobře aproximovat složité průběhy, v takovém případě musíme použít aproximaci polynomem, splinem nebo jinou metodou.
Literatura
- Kočí V.: Několik programů pro kalkulátor Sharp PC-1211. Elektrotechnický Obzor 75, 1985, č. 5–6, s. 301–310
- Djakonov V. P.: Spravočnik po algebram i programmam na jazyke Bejsik dlja personalnych EVM. 1987, Moskva, Nauka, s. 229
DATA 1,1,2,8,3,27,4,64
CLS: DIM m(88): n = 0
za:
z = -4
READ x, y: ON ERROR GOTO v
e = x: f = y: GOTO b
a:
z = z + 5
m(z) = m(z) + x: m(z + 1) = m(z + 1) + y: m(z + 2) = m(z + 2) + x * y
m(z + 3) = m(z + 3) + x * x: m(z + 4) = m(z + 4) + y * y: RETURN
b:
GOSUB a
x = 1 / e: GOSUB a
x = e * e: GOSUB a
x = e: y = 1 / f: GOSUB a
GOSUB a
x = 1 / e: GOSUB a
x = e: y = e / f: GOSUB a
x = e * e: GOSUB a
x = LOG(e): y = LOG(f): GOSUB a
x = e: GOSUB a
GOSUB a
x = 1 / e: GOSUB a
x = e * e: GOSUB a
x = e: y = LOG(f / e): GOSUB a
x = EXP(-e): y = 1 / f: GOSUB a
x = LOG(e): y = f: GOSUB a
n = n + 1: GOTO za
v:
px = m(1) / n: py = m(2) / n
sx = SQR((m(4) – m(1) * m(1) / n) / (n – 1))
sy = SQR((m(5) – m(2) * m(2) / n) / (n – 1))
PRINT "px,py="; TAB(12); px; TAB(28); py
PRINT "sx,sy="; TAB(12); sx; TAB(28); sy
PRINT
z = -4: w = 0
c:
z = z + 5: w = w + 1: IF w > 16 THEN PRINT "KONEC": END
j = m(z + 3) – m(z) * m(z) / n
k = m(z + 4) – m(z + 1) * m(z + 1) / n
c = m(z + 2) – m(z) * m(z + 1) / n
a = (m(z + 1) – c / j * m(z)) / n
b = c / j: r = c / SQR(j * k)
ON w GOTO 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16
1 PRINT "y=a+bx";: GOTO vy
2 PRINT "y=a+b/x";: GOTO vy
3 PRINT "y=a+bx^2";: GOTO vy
4 PRINT "y=1/(a+bx)";: GOTO vy
5 d = a: a = 1 / b: b = a * d: PRINT "y=a/(b+x)";: GOTO vy
6 a = 1 / a: b = a * b: PRINT "y=ax/(b+x)";: GOTO vy
7 PRINT "y=x/(a+bx)";: GOTO vy
8 PRINT "y=x/(a+bx^2)";: GOTO vy
9 a = EXP(a): PRINT "y=a*x^b";: GOTO vy
10 a = EXP(a): b = EXP(b): PRINT "y=a.b^x";: GOTO vy
11 a = EXP(a): PRINT "y=a.exp(bx)";: GOTO vy
12 a = EXP(a): PRINT "y=a.exp(b/x)";: GOTO vy
13 a = EXP(a): PRINT "y=a.exp(bx^2";: GOTO vy
14 a = EXP(a): PRINT "y=ax.exp(bx)";: GOTO vy
15 PRINT "y=1/(a+b.exp(-x))";: GOTO vy
16 PRINT "y=a+b.ln(x)";
vy:
PRINT TAB(20); "a,b,r="; TAB(30); a; TAB(45); b; TAB(60); r
GOTO c
END
z dat na řádku DATA dostaneme:
px,py = 2,5 25
sx,sy = 1,290994 28,22528
| y=a+bx | a,b,r= | -27 | 20.8 | .9513699 |
| y=a+b/x | a,b,r= | 58.97438 | -65.2308 | -.776354 |
| y=a1bx^2 | a,b,r= | -6.976744 | 4.263566 | .9905329 |
| y=1/(a+bx) | a,b,r= | 1.054687 | -.3041088 | -.8304403 |
| y=a/(b+x) | a,b,r= | -3.288297 | -3.468126 | -.8304403 |
| y=ax/(b+x) | a,b,r= | -2.372121 | -3.260907 | .9767918 |
| y=x/(a+bx) | a,b,r= | 1.09375 | -.2951389 | -.8725318 |
| y=x/(a+bx^2) | a,b,r= | .7441053 | -5.17603e-02 | -.7772519 |
| y=a.x^b | a,b,r= | 1 | 3 | 1 |
| y=a.b^x | a,b,r= | .3535533 | 3.932615 | .9801841 |
| y=a.exp(bx) | a,b,r= | .3535533 | 1.369305 | .9801841 |
| y=a.exp(b/x) | a,b,r= | 169.6574 | -5.280461 | -.9835591 |
| y=a.exp(bx^2) | a,b,r= | 1.590411 | .2559397 | .9305829 |
| y=ax.exp(bx) | a,b,r= | .5000002 | .9128695 | .9801837 |
| y=1/(a+b.exp(-x)) | a,b,r= | -.1228715 | 2.921578 | .9762235 |
| y=a+b.ln(x) | a,b,r= | -7.594613 | 41.02462 | .8737795 |
C07 Lineární aproximace funkce
dvou nezávislých proměnných f(x, y)
Je-li závislost z = f(x, y) popsána alespoň čtyřmi trojicemi x, y, z, můžeme těmito body v prostoru proložit rovinu, jejíž rovnice je z = a0 + a1 · x + a2 · y. Použijeme-li metodu nejmenších čtverců, musí být splněna podmínka
Umocněním, úpravami a parciální derivací podle a0, a1, a2 dostaneme charakteristické rovnice
Tyto rovnice řešíme podle a0, a1, a2 pomocí determinantů, což provede následující program, který připraví potřebné sumace a dovoluje i regresní výpočty.
Literatura
- c/s: Slaboproudý Obzor 42, 1981, č. 1, str. 41–42.
- Storm Regina: Wahrscheinlichkeitsrechnung, Mathematische Statistik, Statistiche Qualitatskontrolle. VEB Fachbchverlag Leipzig, 1976, 6.vyd., str. 236–237
DATA 1,3,24,2,8,62,4,6,54,5,12,99
s:
READ x, y, z: ON ERROR GOTO v
sx = sx + x: kx = kx + x * x
sy = sy + y: ky = ky + y * y
sz = sz + z: kz = kz + z * z
xy = xy + x * y: xz = xz + x * z: yz = yz + y * z
n = n + 1: GOTO s
v:
px = sx / n: py = sy / n: pz = sz / n
LPRINT "px,py,pz="; px, py, pz
s1 = SQR((kx – sx * sx / n) / (n – 1))
s2 = SQR((ky – sy * sy / n) / (n – 1))
s3 = SQR((kz – sz * sz / n) / (n – 1))
LPRINT "sx,sy,sz="; s1, s2, s3
a = n * kx – sx * sx: d = n * xy – sx * sy
b = n * ky – sy * sy: e = n * xz – sx * sz
c = n * kz – sz * sz: f = n * yz – sy * sz
a2 = (a * f – d * e) / (a * b – d * d)
a1 = (e – a2 * d) / a
a0 = (sz – a1 * sx – a2 * sy) / n
LPRINT "a0,a1,a2="; a0, a1, a2
r1 = SQR(d * d / (a * b)): r2 = SQR(e * e / (a * c))
r3 = SQR(f * f / (b * c))
LPRINT "rxy,rxz,ryz="; r1, r2, r3
r:
INPUT "x,y="; x, y: LPRINT "x,y="; x, y
z = a0 + a1 * x + a2 * y
LPRINT "z="; z
GOTO r
LPRINT
END
z dat v řádku DATA dostaneme:
px,py,pz = 3 7.25 59.75
sx,sy,sz = 1.825742 3.774917 30.85855
a0,a1,a2 = 0 3 7
rxy,rxz,xyz =.7738413.8401411.9936606
x,y=
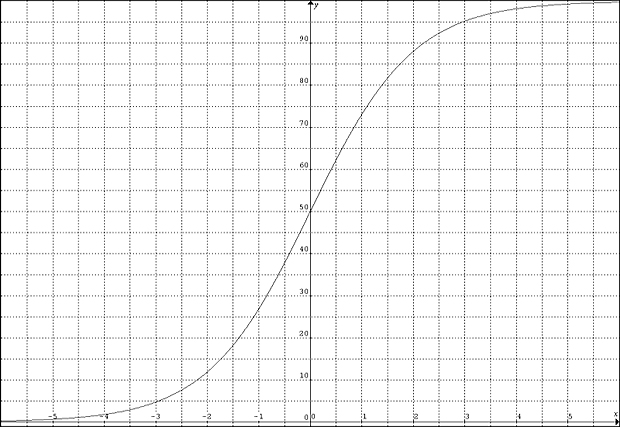
C08 Aproximace vývojové křivky sportovního výkonu
Vývoj biologických objektů nejlépe popisuje Robertsonův zákon růstu, který je popsán vzorcem
Křivka, zobrazující tento zákon, má tvar podle obr. C08b
Ve sportu musíme rozlišovat vývoj, v němž výsledky
rostou (atletické skoky, hody a vrhy, vzpírání, u lokomočních sportů hodinovky a časově omezené výkony),
klesají jako časy ve všech lokomočních sportech (běhy, chůze, cyklistika, rychlobruslení, plavání, veslování a vodácké sporty)
U první skupiny můžeme tabulku věk-výkon aproximovat uvedenou funkcí, kdy a, b vypočítáme prvním programem, u druhé skupiny musíme tabulku věk-čas přepočítat na věk-rychlost, provést aproximaci druhým programem, který vypočítá a, b pro závislost
Oba programy pak dovolují regresní výpočty pro zvolený věk.
Literatura
- Technický průvodce Matematika, Praha, ČMT, 1944, str. 318
- Návod k počítači SHARP PC-1500, str. 47
Program 1
DATA v1,L1,v2,L2,… vn,Ln
INPUT "Lmax=";k
a:
READ v,L: ON ERROR GOTO b
y=log(k/L-1)
e=e+v
f=f+v*v
g=g+y
h=h+y*y: n=n+1
GOTO a
b:
b=n*f-e*e
a=(f*g-e*h)/b
b=(n*h-e*g)/b
a=EXP(a): b=-b
PRINT "a,b=";a,b
c:
INPUT "vek";x
y=k/(1+a*exp(-b*x))
PRINT "výkon=";y
GOTO c: END
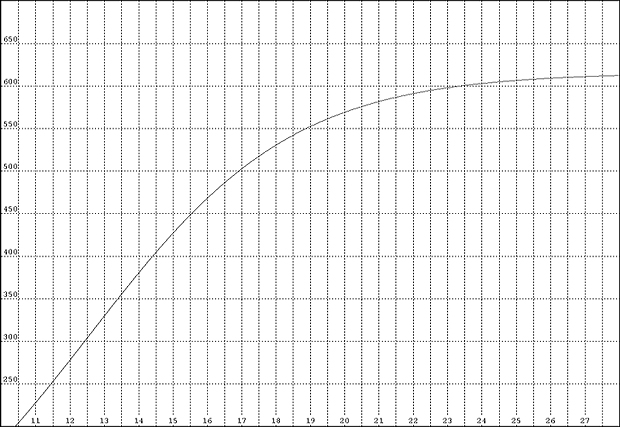
S.Bubka se vyvíjel ke světovému rekordu ve skoku o tyči podle této tabulky:
| věk | výkon |
|---|---|
| 12 | 270 |
| 14 | 360 |
| 16 | 480 |
| 18 | 540 |
| 20 | 572 |
| 22 | 600 |
| 24 | 603 |
| 26 | 600 |
| 28 | 612 |
| 30 | 615 |
| 20 | 569 |
| 22 | 591 |
| 24 | 603 |
| 26 | 609 |
| 28 | 612 |
| 30 | 614 |
Zvolíme-li Hmax = 616 cm, dostaneme programem aproximační funkci
H = 616 / (1 + 69.7286*exp(-0.3374459617))
a regresními výpočty tabulku:
| věk | výkon |
|---|---|
| 12 | 278 |
| 14 | 380 |
| 16 | 460 |
| 18 | 530 |
Program 2
DATA v1,t1,v2,t2,….vn,tn
INPUT "trať,nejl.čas=";L,k
w=L/k
a:
READ v,t: ON ERROR GOTO b
y=log(w*t/L-1)
e=e+v
f=f+v*v
g=g+y
h=h+y*y: n=n+1
GOTO a
b:
b=n*f-e*e
a=(f*g-e*h)/b
b=(n*h-e*g)/b
a=exp(a): b=-b
PRINT "a,b=";a,b
c:
INPUT "věk=";x
t=k*(1+a*exp(-b*x))
PRINT "čas=";t
GOTO c
END
britský sprinter L.Christie se
vyvíjel podle této tabulky:
| věk | čas(100m) | rychlost(m/s) |
|---|---|---|
| 17 | 10,9 | 9.174 |
| 20 | 10.73 | 9.319 |
| 22 | 10.5 | 9.524 |
| 24 | 10.44 | 9.5765 |
| 26 | 10.04 | 9.96 |
| 28 | 9.97 | 10.03 |
| 30 | 10.02 | 9.98 |
| 33 | 9.87 | 10.13 |
t= 9.85.(1+9.221385.exp(-0.232872))
a tabulku regresních časů:
| věk | čas |
|---|---|
| 17 | 11.58 |
| 20 | 10.71 |
| 22 | 10.39 |
| 24 | 10.19 |
| 26 | 10.06 |
| 28 | 9.98 |
| 30 | 9.93 |
| 33 | 9.89 |
C09 Graf funkce
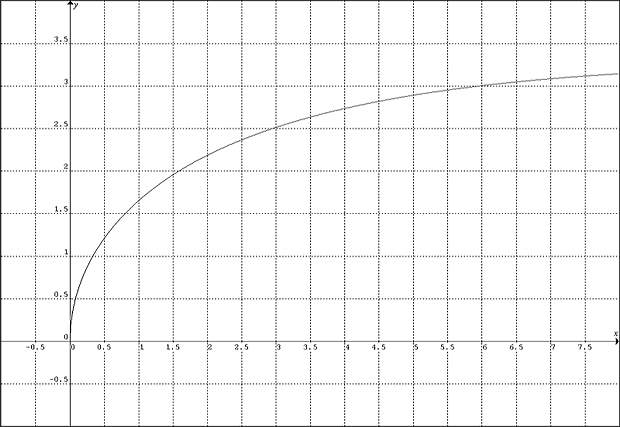
Známe-li rovnici nějaké křivky y = f(x), můžeme potřebovat pro názornost nakreslit průběh této funkce v určitém intervalu hodnot nezávislé proměnné x. Následující program provede tuto úlohu, vložíme-li za label g rovnici funkce, po spuštění pak vložíme rozsah x, program stanoví rozsah y, který můžeme změnit a nakonec se objeví průběh funkce s popisem rozsahů.
INPUT "xmin,xmax="; x1, x2
y1 = 1000000!: y2 = -1000000!
FOR x = x1 TO x2 STEP (x2 – x1) / 100
GOSUB g: IF y < y1 THEN y1 = y
IF y > y2 THEN y2 = y
NEXT x
PRINT "ymin,ymax="; y1, y2
INPUT "zmena ymin,ymax? a/n"; a$: IF a$ <> "a" THEN GOTO b
INPUT "ymin,ymax="; y1, y2
b:
SCREEN 10: CLS: KEY OFF
PRINT "xmin,xmax="; x1, x2
PRINT "ymin,ymax="; y1, y2
x = x1 / (x1 – x2) * 640
IF x1 * x2 <= 0 THEN LINE (x, 50)-(x, 320)
y = 320 – y1 / (y1 – y2) * 260
IF y1 * y2 <= 0 THEN LINE (o, y)-(640, y)
x = x1: GOSUB g: PSET (x, 320 – (y – y1) / (y2 – y1) * 260)
FOR x = x1 TO x2 STEP (x2 – x1) / 100
GOSUB g
LINE -((x – x1) / (x2 – x1) * 640, 320 – (y – y1) / (y2 – y1) * 260), 12
NEXT x
END
g:
y = SQR(x) / (.0042095 * x +.562045)
RETURN
funkci y= sqr(x)/(.042095*x + 0.562045), připsanou za label g zobrazí program grafem, který následuje.
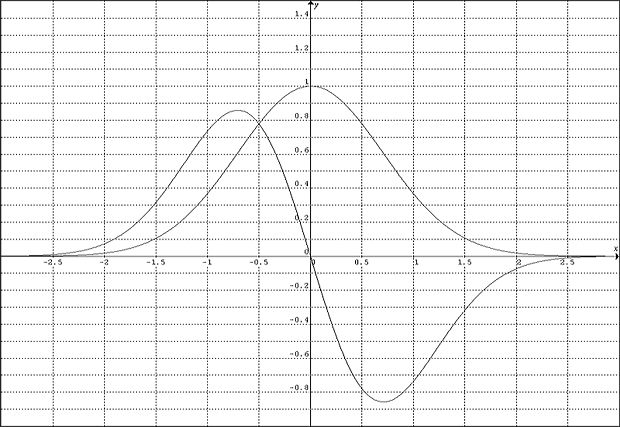
C10 Graf funkce a její derivace
Máme-li dánu funkci analytickým výrazem y = f(x) a má-li derivace této funkce význam – derivace dráhy dle času je rychlost, derivace rychlosti podle času je zrychlení – může být zajímavý graf funkce a její derivace. Takový graf můžeme získat následujícím programem, který musíme doplnit za labelem g podprogramem, definujícím funkci ve formě y = f(x).
Program vyžádá rozsah nezávislé proměnné x, zjistí rozsah závislé proměnné y a zeptá se, zda tento rozsah chceme změnit. Souhlas se změnou vyjádříme písmenem a, vložíme jiné meze y a program zobrazí průběh funkce a její derivace, která se počítá numericky vztahem
bod za bodem. Funkce a její derivace jsou odlišeny barevně, funkce je nakreslena červenou čarou, derivace modrou.
INPUT "xmin,xmax="; x1, x2
y1 = 1000000!: y2 = -1000000!
FOR x = x1 TO x2 STEP (x2 – x1) / 100
GOSUB g: IF y < y1 THEN y1 = y
IF y > y2 THEN y2 = y
NEXT x
PRINT "ymin,ymax="; y1, y2
INPUT "zmena ymin,ymax? a/n"; a$
IF a$ <> "a" THEN GOTO a
INPUT "ymin,ymax="; y1, y2
a:
SCREEN 9: CLS: KEY OFF
PRINT "xmin,xmax="; x1, x2
PRINT "ymin,ymax="; y1, y2
PRINT "funkce cervena,derivace modra"
x = x1 / (x1 – x2) * 640
IF x1 * x2 <= 0 THEN LINE (x, 50)-(x, 320)
y = 320 – y1 / (y1 – y2) * 260
IF y1 * y2 <= 0 THEN LINE (0, y)-(640, y)
x = x1: GOSUB g: PSET (x, 320 – (y – y1) / (y2 – y1) * 260), 4
d = (x2 – x1) / 300: x0 = x: y0 = y
FOR x = x1 + d TO x2 STEP d: GOSUB g
CIRCLE ((x – x1) / (x2 – x1) * 640, 320 – (y – y1) / (y2 – y1) * 260), 2, 12
de = (y – y0) / d
CIRCLE ((x – x1) / (x2 – x1) * 640, 320 – (de – y1) / (y2 – y1) * 260), 2, 9
y0 = y: NEXT x
END
g:
y = EXP(-x * x)
RETURN
zapíšeme-li za label g funkci y = exp(-x*x), dostaneme pro rozsah
x od -3 do 3 následující graf.
Fakulta sportovních studií, Masarykova univerzita |
Návrat na úvodní stránku webu, přístupnost |
| Servisní středisko pro e-learning na MU
| Fakulta informatiky Masarykovy univerzity, 2011
Technické řešení této výukové pomůcky je spolufinancováno Evropským sociálním fondem a státním rozpočtem České republiky.