Sport, matematika, počítač
Fakulta sportovních studií Masarykovy univerzity
Ing. Josef Kopřiva

Kliknutím na šedou plochu pod nápisem se vrátíte zpět nahoru

G. Mechanika

část G01–G04

G01 Parabolická dráha ve sportu

Parabolická dráha je nejčastějším případem dráhy těžiště buď sportovcova těla nebo letícího předmětu, je-li možno zanedbat odpor vzduchu (viz kapitola I01 – Mezní rychlost pádu). Jsou to tyto případy:

běžec nebo skokan ve fázi letu (ničeho se nedotýká)

koule v lehké atletice (ostatní nářadí nikoliv)

míče s velkou mezní rychlostí na krátké dráze.

V ostatních případech, kdy odporem vzduchu rychle klesá rychlost, (stolní tenis, badminton) se musí počítat dráha jako balistická.

Nejsložitější případy, kdy pohyb ovlivňuje i vztlak vzduchu (hod diskem, skok na lyžích), nedovolují přesnější výpočet dráhy vůbec.

Rovnici dráhy pro vztah mezi souřadnicemi y = f(x) odvodíme nejsnadněji z parametrických rovnic, v nichž parametrem je čas t:

vodorovná souřadnice

$x=v.\cos{\alpha}.t$

svislá souřadnice

$y=h+v.\sin{\alpha}.t-0,5.g.t^2$

kde

v … počáteční rychlost (m/s)

a … počáteční úhel dráhy

h … výška počátečního bodu dráhy (m)

t … čas (s)

g … gravitační zrychlení (9,80665 m²/s)

Čas z první rovnice

$t=\frac{x}{v}.\cos\alpha$

dosadíme do druhé a tím jej vyloučíme:

$y=h+v.\sin\alpha.\frac{x}{v.\cos\alpha}-4,9033.\frac{x^2}{(v.\cos\alpha)^2}$

$=h+x.\tan\alpha-4,9033.\frac{x^2}{(v.\cos\alpha)^2}$

$=c+b.x+a.x^2$

Porovnáním posledních dvou rovnic bude

$c=h$

$b=\tan\alpha$

$=a=\frac{-4,9033}{(v.\cos\alpha)^2}$

Pro určitou parabolickou dráhu známe většinou tři dvojice souřadnic těžiště těla nebo míče x, y: pro začátek dráhy, pro místo, blízké středu dráhy a pro konec dráhy (většinou dopad). Z těchto dvojic je snadné vypočítat činitele a, b, c metodou nejmenších čtverců a posledními vzorci vypočítat

$\alpha=\arctan{b}$

$v=(\frac{-4.9033}{a.\cos^2{\alpha}})^{1/2}$

Zajímá-li nás vrchol dráhy, dané rovnicí y = ax² + bx + c, použijeme derivaci, kterou položíme rovnu 0:

$y'=2.a.x+b=0$

Odtud pak

$x_m=\frac{-b}{2a}$

$y_m=a.x_m^2+b.x_m+c$

Známe-li počáteční rychlost v, jejíž směr je dán úhlem a, pak vodorovná rychlost je v_x = v · cos a, a z vodorovné délky dráhy x₃ můžeme počítat dobu letu: T = x₃ / v_x. Pro basketbal je zajímavý i směr dráhy při dopadu. Určíme jej ze složek rychlosti v_y, v_x kde v_y = v · sin a – 9,80665. T, a vodorovná rychlost v_x = v · cos a se prakticky nemění. Pak úhel dopadu

$\tan\alpha=\frac{v_y}{v_x}=\frac{(v.\sin\alpha-9.80665.T)}{v.\cos\alpha}$

Program, který ze tří vložených dvojic souřadnic vypočítá všechny zde uvedené veličiny je tento:


PRINT: PRINT

DATA 0,2.2,1.7,5,3.225,3.05

FOR w = 1 TO 3: READ x, y: PRINT x, y: NEXT w

RESTORE

a:

READ x, y: ON ERROR GOTO b

d = d + x: k = x * x: e = e + k: f = f + x * k: g = g + k * k

h = h + y: i = i + x * y: j = j + y * k: n = n + 1: GOTO a

b:

l = e – d * d / n: m = i – d * h / n: o = f – d * e / n: p = j – e * h / n

q = g – e * e / n: r = l * q – o * o: a = (p * l – m * o) / r

b = (m * q – p * o) / r: c = (h – b * d – a * e) / n

PRINT "a,b,c="; a; " "; b; " "; c

u = ATN (b): v = SQR (-4.905 / (a * COS (u) * COS (u)))

PRINT "alfa,v0="; u * 57.29578; " "; v

xm = -b / (2 * a): ym = (a * xm + b) * xm + c

PRINT "xm,ym="; xm; " "; ym

RESTORE: FOR w = 1 TO 5: READ x: NEXT w

t = x / (v * COS (u)): PRINT "T="; t

be = ATN ((v * SIN (u) – 9.81 * t) / (v * COS (u)))

PRINT "uhel dopadu="; be * 57.29578

c:

INPUT "x="; x: y = (a * x + b) * x + c: PRINT "y="; y: GOTO c

END

Poslední část od labelu c dovoluje regresní výpočty bodů trajektorie.

Příklad:

skok vysoký přes laťku ve výšce 2.35 bude mít DATA:

x	y
0	1.3
1.6	2.4
3.5	1.0

Dostaneme:

a,b,c= -0.406954 1.33827 1.3
alfa,v0 = 53.339032° 5.800937 m/s
xm,ym = 1.644688 m, 2.400812 m, T=1.008141 s, beta= -59.71058°

Příklad:

skok daleký 7.8 m může mít DATA:

x	y
0	1.3
4	1.8
7.8	0.45

Výsledky:

a,b,c = -0.061572 0.371288 1.3
alfa,v0 = 20.369397° 9.520739 m/s
xm,ym = 3.015069 m, 1.859730 m, T=0.873911 s, beta= -42.035856°

Příklad:

vrh koulí 20 m:

x	y
0	2.2
10	6
20	0

Výsledky:

a,b,c = -0.049 0.87 2.2
alfa,v0 = 41.023° 13.26 m/s
xm,ym= 8.877 m, 6.06 m, T= 1.999 s, beta = -55.9°

Příklad:

trestný hod v basketbalu:

x	y
0	2
2.1	4
4.225	3.05

Výsledky:

a,b,c=-0.331228 1.647960 2.0
alfa,v0= 58.75° 7.418 m/s
xm,ym = 2.48765 m, 4.05 m, T = 1.0979 s, beta= -55,55°

Nahoru

G02 Optimální počáteční úhel parabolické dráhy

Z parametrických rovnic parabolické dráhy

$x=v.t.\cos\alpha$

$y=h+\frac{v.t.\sin\alpha.g.t^2}{2}$

můžeme eliminovat čas t = x / (v · cos a) a dostaneme vztah mezi x, y:

$y=h+\frac{x.\sin\alpha}{\cos\alpha}-\frac{g.x^2}{2.v^2.cos^2\alpha}$

V místě dopadu x = L, y = 0:

$0=h+\frac{L.\sin\alpha}{\cos\alpha}-\frac{g.L^2}{2.v^2.cos^2\alpha}$

Násobením 2 · v² · cos²a dostaneme

$2.h.v^2.\cos^2\alpha+2.L.v^2.\sin\alpha.\cos\alpha=g.L^2$

S trigonometrickou identitou 2 · sina · cosa = sin 2a

$2.h.v^2.\cos^2\alpha.L.v^2.\cos{2\alpha}=g.L^2$

Maximum délky L je funkcí počátečního úhlu a a najdeme je derivováním poslední rovnice podle a:

$-4.h.v^2.\cos\alpha.\sin\alpha+2.L.v^2.\cos{2\alpha}=0$

$h.\sin{2\alpha}=L.\cos{2\alpha}$

$\tan{2\alpha}=\frac{L}{h}$

Optimální úhel

$\alpha=0,5\arctan{\frac{L}{h}}$

Tento vzorec byl použit k výpočtu následující tabulky pro vrh koulí:

L(m)
	10	12	14	16	18	20	22	24
2	39,3	40,3	40,9	41,4	41,8	42,1	42,4	42,6
2,1	39,1	40	40,7	41,3	41,7	42	42,3	42,5
2,2	38,8	39,8	40,5	41,1	41,5	41,9	42,1	42,4
2,3	38,5	39,6	40,3	40,9	41,4	41,7	42	42,3
2,4	38,3	39,3	40,1	40,7	41,2	41,6	41,9	42,1

Z tabulky vyplývá pravidlo:

Čím větší délka vrhu a menší výška počátečního bodu, tím více se optimální úhel blíží 45°.

V literatuře najdeme vzorce pro výpočet optimálního úhlu, je-li známa počáteční rychlost v, kterou ale nutno měřit.

Lampe uvádí vzorec

$\alpha_{opt}=\arcsin{\frac{v}{\sqrt{2.(v^2+g.h)}}}$

Townend

$\alpha_{opt}=0,5.\arccos{\frac{g.h}{v^2+g.h}}$

Závěrem je nutné poznamenat, že jediný případ parabolické dráhy je vrh koulí, protože u něj můžeme zanedbat odpor vzduchu. U ostatních hodů je rychlost příliš vysoká a dráha příliš dlouhá, takže je balistická, tzn. vlivem odporu vzduchu o něco zkrácená oproti parabolické.

Literatura

Kopřiva J.: Optimální úhel hodů a vrhů. TPTV 16, 1968, 4, s. 251
Lampe E.: Mathematik und Sport. 1956, B. G. Teubner, Leipzig, s. 16
Townend M. S.: Mathematics in sport. 1984, Ellis Horwood, Chichester, s. 45.

Nahoru

G03 Parabolická dráha a měření času

V kapitole G01 jsme stanovili parametry parabolické dráhy ze souřadnic 3 bodů této dráhy. Při televizních přenosech nebývá možné stanovit souřadnice druhého bodu někde uprostřed dráhy, zato je snadné změřit dobu letu koule nebo dálkaře. Pokud je dosažena přesnost kolem 0,01 sek, můžeme použít následující metodu. Potřebujeme znát vodorovnou délku parabolické dráhy (měřený výsledek u koule, výsledek dálkaře, korigovaný na sklon při odrazu a dopadu), pokles těžiště během letu H₀ a trvání letu. Pak plyne z Pythagorovy věty (obr. G03)

$(v.T)^2=(\frac{1}{2}.g.T^2-H_0)^2+L^2$

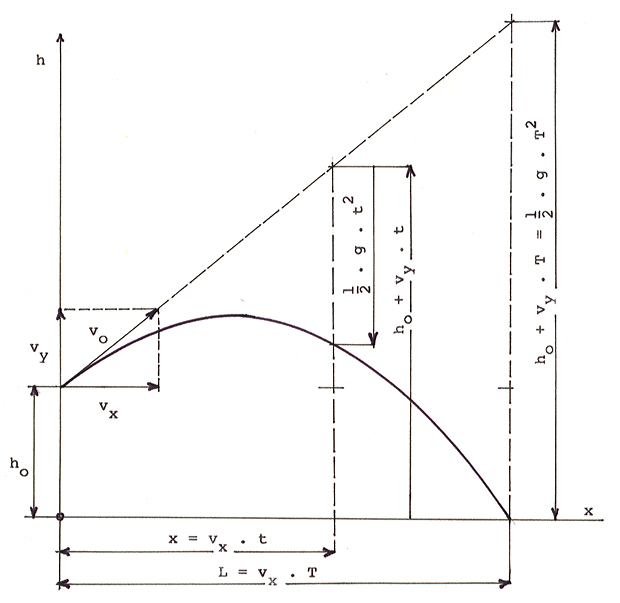
Obr. G03: Podklad pro aplikaci Pythagorovy věty

Odtud počáteční rychlost

$v^2=\frac{\sqrt{(4,905.T^2-H_0)^2+L^2}}{T}$

vodorovná složka rychlosti

$v_x=\frac{L}{T}$

počáteční úhel dráhy

$a=\arccos{\frac{v_x}{v}}$

Pro počítače bez arc cos

$p=\frac{v_x}{v}$

a počáteční úhel

$a=\arctan{\frac{\sqrt{1-p^2}}{p}}$

Použijeme program v Qbasicu:


INPUT "H0=";H

a:

INPUT "L,T="; L,T

vx=L/T

v=SQR((4.905*T*T-H0)^2+L*L)/T

p=vx/v

a=ATN(SQR(1-p*p)/p)*57.296

PRINT "v,alfa=";v,a

GOTO a

Příklad 1:

vítěz ve vrhu koulí na OH 1988 Ulf Timmerman (NDR) měl při vrhu délky L= 22,02 m naměřen čas T = 1,97 s. Pro výšku počátečního bodu H₀ = 2,3 m dostaneme v = 14,04 m/s a úhel 37,24°. Optimální úhel podle G02 je 42,02° a pro něj by byl vrh dlouhý L = 22,276 m, tedy o 0,25 m delší.

Příklad 2:

na mistrovství světa 1987 v Římě skočili do dálky
Carl Lewis (USA) L=8,67 m, T=0,89 s, v=10,418 m/s, a=20,75°
Robert Emmjan (SSSR) L=8,49 m, T=0,97 s, v=8,934 m/s, a=27,57°
(před výpočtem byla délka korigována na vodorovnou dráhu těžiště o dL=0,8 m,
pokles těžiště odhadnut na 0,7m)

Ze srovnání rychlostí a úhlů vyplývá známá skutečnost, že Lewis byl sprinterský skokan do dálky, a Emmjan odrazový.

Nahoru

G04 Dostředivá a odstředivá síla

V případě rychlého křivočarého pohybu (běh, rychlobruslení, cyklistika a motocyklové závody, lyžování, hod diskem nebo kladivem apod.) musí existovat dostředivá síla, protože jinak by pohyb byl lineární (Newtonův I. zákon). Avšak Newtonův III. zákon říká, že musí ke každé akci existovat reakce, a tou je odstředivá síla. Výpočet obou těchto sil je poměrně jednoduchý. Z obr. G04 lze odvodit následující vztahy:

$v_2=v_1+d_v$

$r_2=r_1+d_r$

$\frac{d_v}{v}=\frac{d_r}{r}$

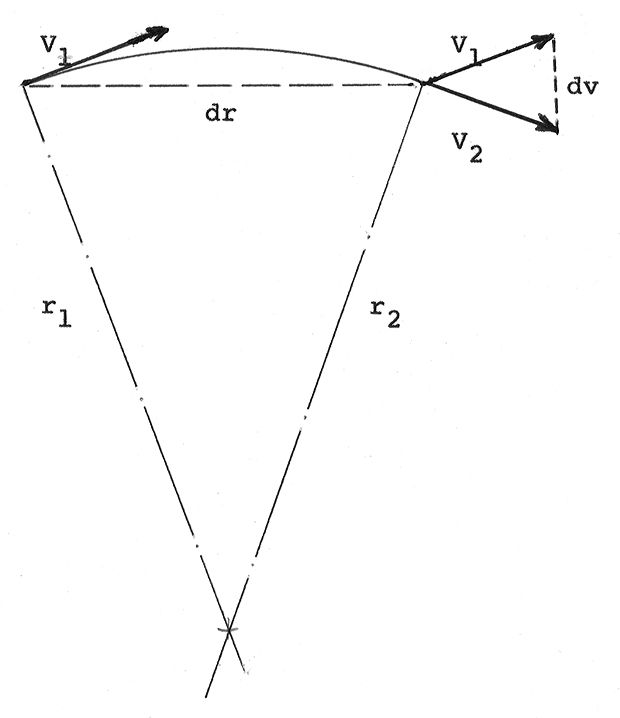
Obr. G04: Podklad pro aplikaci odvození vzorců

Pak

$d_v=\frac{v}{r.d_r}$

a dělením dt

$a_r=\frac{d_v}{d_t}=\frac{v.d_r}{r.d_t}=\frac{v^2}{r}$

Je-li radiální zrychlení ar, pak dostředivá síla je

$F_r=m.a_r=\frac{m.v^2}{r}=m.w^2.r$

kde úhlová rychlost

$w=\frac{v}{r}$

Odstředivá síla je

$F_c=-F_r$

Příklad:

běžec s rychlostí v = 10 m/s v zatáčce s r = 31,8 m a hmotností m = 75 kg musí vytvořit dostředivou sílu F = 75 · 102 / 31,8 = 235,8 newtonů a musí se naklonit směrem do středu zatáčky s úhlem a = arc tan(F / m · g) = 17,77° ke svislé rovině.

Mimořádně velké úhly musí mít motocyklový závodník v zatáčce malého poloměru při vysoké rychlosti:

v	v	poloměr (m)
km/h	m/s	50	75	100	150	200
100	27,77	57,57	46,37	38,18	27,7	21,4
120	33,33	66,19	56,5	48,57	37,06	29,5
140	38,89	72,04	64,06	57,04	45,8	37,6
160	44,44	75,06	69,6	63,6	53,3	45,2
180	50	78,9	73,6	68,58	59,5	51,9
200	55,56	81	76,6	72,37	64,5	57,5

Tyto úhly musí být vzaty v úvahu při konstrukci pneumatik, stupaček a obrysu motocyklu.

autor: Ing. Josef Kopřiva, recenzent: Mgr. Martin Sebera, Ph.D. |
Fakulta sportovních studií, Masarykova univerzita |
Návrat na úvodní stránku webu, přístupnost |

| Technická spolupráce:
| Servisní středisko pro e-learning na MU
| Fakulta informatiky Masarykovy univerzity, 2011

Technické řešení této výukové pomůcky je spolufinancováno Evropským sociálním fondem a státním rozpočtem České republiky.

Nahoru

INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ