G. Mechanika
část G05–G09
G05 Záznam časového průběhu svalové síly
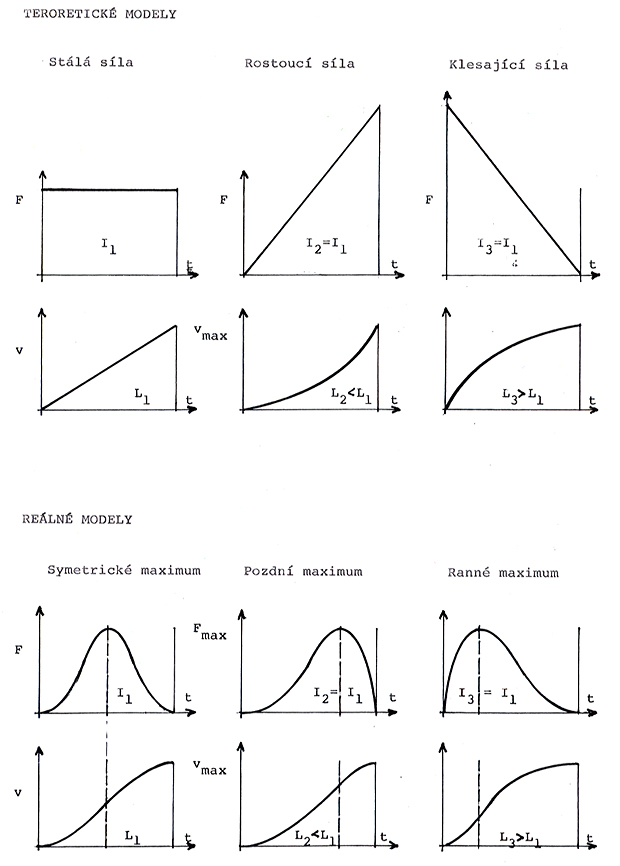
V řadě explosivních sportovních disciplin urychluje sportovec buď své tělo (skoky) nebo nářadí (vrhy a hody). Používá k tomu výbušné síly, která v krátkém okamžiku vzroste z nuly na maximum a pak klesá zpět na nulu. Bude-li impuls síly
konstantní, pak při jakémkoliv časovém průběhu síly bude konečná rychlost stejná, protože je v = I / m. Časový průběh má ale vliv na jinou významnou veličinu – dráhu. Průběh může být
- časově souměrný
- s časným maximem
- s pozdním maximem
Z grafů G05 vyplývá tento závěr:
čím později dosáhne urychlující síla svého maxima (při stejném impulsu), tím kratší je dráha, potřebná k dosažení stejné maximální rychlosti. Protože v praxi je tato dráha vždy omezená, je pro sportovce výhodné používat sílu tak, aby její maximum bylo dosaženo co nejpozději, tedy explosivně vystupňované. K tomu musí být zaměřen také posilovací trénink.
G06 Moment setrvačnosti
Tento moment, významný pro mechaniku otáčivého pohybu si vysvětlíme analogií mezi pohybem posuvným a otáčivým (translačním a rotačním).
Při posuvném pohybu jsou dráhy všech bodů tělesa stejné, ať přímkové nebo křivkové. Příklady: jízda na saních po přímé dráze, sjezd lyžaře ve stálé poloze.
Při otáčivém pohybu jsou dráhy všech bodů tělesa kružnice se středy na ose otáčení. Příklady: pirueta krasobruslaře ve stálé poloze těla, veletoč gymnasty při stálém držení těla.
Naprostá většina sportovních pohybů jsou pohyby složené z posuvných a otáčivých. Příklady: noha cyklisty se otáčí okolo osy pedálů a posouvá s bicyklem, (výsledná dráha je zkrácená cykloida), tělo skokana do vody se může otáčet okolo podélné osy (vruty) i příčné osy (překoty) a při tom posuvným pohybem padá po parabolické dráze, diskař nebo kladivář provádí otočky kolem své osy a při tom se posouvá k bodu odhodu.
Moment setrvačnosti při otáčivém zrychlování nebo zpomalování má obdobný vliv jako hmotnost při pohybu posuvném:
| Posuv | Otáčení | ||
|---|---|---|---|
| Síla | F = m · a | moment síly | M = I · ε |
| Zrychlení | a = F / m | úhlové zrychlení | ε = M / I |
Při posuvném pohybu brání zrychlování hmotnost tělesa m,
při otáčivém pohybu brání zrychlování moment setrvačnosti I.
Pro těleso, skládající se z jednoduchých částí o hmotě mi, které mají těžiště na poloměru ri od osy otáčení je moment setrvačnosti dán součtem
Při tvaru daném nějakou závislostí musíme integrovat:
Momenty setrvačnosti lidského těla pro průměrnou velikost těla jsou v tabulce:
| Poloha těla | osa | prochází |
moment setrvačnosti (kg · m2) |
|---|---|---|---|
| vzpřímená připažená | svislá | těžištěm | 1 – 1,5 |
| vzpřímená upažená | svislá | těžištěm | 2 – 2,5 |
| dřep | svislá | těžištěm | 2,3 |
| dřep | příčná | těžištěm | 4,5 – 6 |
| vzpřímená připažená | příčná | těžištěm | 10,5 – 13 |
| vzpřímená připažená | předozad. | těžištěm | 12 – 15 |
| vzpřímená vzpažená | příčná | těžištěm | 15 – 18 |
| vzpřímená vzpažená | příčná | dlaněmi | 85 – 90 |
Známe-li moment setrvačnosti v nějaké poloze, pak k ose posunuté o vzdálenost d bude moment setrvačnosti Id = I + m · d2. Tento vzorec vyjadřuje tzv. Steinerovu větu. Tento vztah platí pro poslední dva případy v tabulce, kdy osa byla přemístěna z těžiště do dlaní.
Zatím co hmotnost těla sportovec změnit nemůže, moment setrvačnosti změnit lze, jak vidíme z tabulky. Protože platí zákon o zachování energie Ekin = 0,5 · m · v2 pro pohyb posuvný, pro pohyb otáčivý platí Ekin = 0,5 · I · ω2
Změní-li se moment setrvačnosti z I1 na I2, změní se úhlová rychlost z w1 na w2 a protože energie zůstane nezměněna, bude poměr úhlových rychlostí ω1 / ω2 = (I2 / I1)0,5.
Tak si lze vysvětlit zrychlení piruety krasobruslaře, který přitáhne paže k tělu a zmenší tak moment setrvačnosti. Podobně může měnit rychlost otáčení skokan do vody: připažením zrychlí vruty, polohou skrčeně pak překoty.
Moment setrvačnosti tedy potřebujeme k vysvětlení některých změn otáčivých pohybů v krasobruslení, gymnastice, skocích do vody a podobných sportech.
G07 Analogie mezi translačním a rotačním pohybem
| translace | rotace |
|---|---|
| a) ustálený stav (d / dt=0) | |
| dráha s = v · t | otočení (úhel) a = w · t |
| rychlost v = s / t | úhlová rychlost w = a / t |
| zrychlení a = v / t | úhlové zrychlení e = w / t |
| setrvačná hmota m | moment setrvačnosti I= r2 · dm |
| II. Newtonův zákon | |
| síla setrvačnosti F = m · a | moment síly M = I · e = F · r |
| zrychlení a = F / m | úhlové zrychlení e = M / I |
| hybnost H = m · v | rotační hybnost H = I · w |
| impuls síly I = F · t | rotační impuls R = M · t |
| rovnost impulsu a změny hybnosti | |
| I = H2 – H1 = m · (v2 – v1) | R = H2 – H1 = I · (w2 – w1) |
| práce síly A = F · s | práce momentu A = M · a |
| pohybová (kinetická) energie | |
| E = m · v2 / 2 | E = I · w2 / 2 |
| rovnost práce síly a změny kinetické energie | |
| A = E2 – E1 = m · (v22 – v12) | A = I · (w22 – w12) |
| výkon síly N = A / t = F · v | N = A / t = M · w |
| b) neustálený stav (d / dt <> 0) | |
| dráha ds = v(t) · dt | otočení da = w(t) · dt |
| rychlost v(t) = ds / dt | úhlová rychlost w(t) = da / dt |
| zrychlení a(t) = dv / dt | úhlové zrychlení e(t) = dw / dt |
| impuls proměnlivé síly dI = F(t) · dt | proměnlivého momentu dI = M(t) · dt |
| práce proměnlivé síly dA = F(t) · ds = F(t) · v(t) · dt | proměnlivého momentu dA = M(t) · da = M(t) · w(t) · dt |
| výkon N(t) = dA / dt = F(t) · v(t) | N(t) = dA / dt = M(t) · w(t) |
Pozn: d / dt je symbol derivace podle času, d diferenciál, veličiny se závorkou (t) jsou veličiny časově proměnlivé, a proto je nutno jejich součin s jinou veličinou, také proměnlivou integrovat v čase. Součin těchto veličin dává okamžitou hodnotu, také proměnlivou v čase.
G08 Vztah mezi hmotností a svalovou silou sportovce
Tělesná hmotnost při stálé průměrné hustotě těla je úměrná objemu těla
Objem těla je při stálém tvaru těla úměrný třetí mocnině tělesné výšky
a tedy i hmotnost
Inversně
Svalová síla při stálém svalovém napětí je úměrná průřezu svalu
Průřez svalu jako plocha je úměrný druhé mocnině tělesné výšky
a tedy i síla
dosazením
Úměrnost můžeme nahradit konstantou úměrnosti
Konstanta úměrnosti
závisí na kvalitě a trénovanosti svalu, věku, pohlaví, teplotě atd. Platnost tohoto vztahu můžeme ověřit na světových rekordech ve vzpírání pro různé váhové kategorie. Použít k tomu můžeme dvě tabulky světových rekordů: jednu k 31.12.1992, uzavřenou před změnami váhových kategorií, a druhou k 1.8.1998 s novými váhovými kategoriemi. Dostaneme tabulky, v nichž c1 je konstanta úměrnosti pro trh, c2 pro nadhoz a c3 pro dvojboj.
Ke dni 31. 12. 1992:
| m(kg) | trh | c1 | nadhoz | c2 | dvojboj | c3 |
|---|---|---|---|---|---|---|
| 52 | 121 | 8,685 | 155 | 11,126 | 272,5 | 19,560 |
| 56 | 135 | 9,223 | 171 | 11,682 | 300 | 20,496 |
| 60 | 152,5 | 9,950 | 190 | 12,397 | 342,5 | 22,347 |
| 67,5 | 162,5 | 9,802 | 200,5 | 12,094 | 355 | 21,414 |
| 75 | 170 | 9,559 | 215,5 | 12,117 | 382,5 | 21,507 |
| 82,5 | 183 | 9,656 | 225 | 11,873 | 405 | 21,371 |
| 90 | 192,5 | 9,585 | 235 | 11,701 | 422,5 | 21,038 |
| 100 | 200,5 | 9,306 | 242,5 | 11,256 | 440 | 20,423 |
| 110 | 210 | 9,147 | 250,5 | 10,911 | 455 | 19,819 |
| (135) | 216 | 8,208 | 266 | 10,108 | 475 | 18,050 |
Ke dni 1.8.1998:
| m(kg) | trh | c1 | nadhoz | c2 | dvojboj | c3 |
|---|---|---|---|---|---|---|
| 54 | 132,5 | 9,274 | 162,5 | 11,374 | 290 | 20,300 |
| 59 | 147,5 | 9,732 | 170 | 11,217 | 307,5 | 20,290 |
| 64 | 151,5 | 9,469 | 187,5 | 11,719 | 335 | 20,937 |
| 70 | 163 | 9,597 | 200,5 | 11,804 | 360 | 21,195 |
| 76 | 170 | 9,475 | 208 | 11,593 | 372,5 | 20,761 |
| 83 | 180 | 9,460 | 214 | 11,247 | 392,5 | 20,628 |
| 91 | 187,5 | 9,268 | 228,5 | 11,294 | 414 | 20,463 |
| 99 | 192,5 | 8,995 | 235 | 10,981 | 420 | 19,626 |
| 108 | 200 | 8,819 | 235,5 | 10,384 | 435 | 19,181 |
| (135) | 205,5 | 7,809 | 262 | 9,956 | 465 | 17,670 |
Pozn.: nejtěžší váhy nad 110 a 108 kg byly odhadnuty číslem (135).
Z obou tabulek plyne, že:
- staré a dnes neplatné rekordy k 31.12.1992 byly vyrovnanější, protože průběh hodnot c1, c2, c3 je plynulý. Ukazuje totiž delší historický vývoj, nežli nové rekordy, vyvíjející se teprve n2kolik let (od 1.1.1993).
- nejlepší ukazatele mají střední váhové kategorie mezi 60–70 kg, protože u nižších vah je konkurence (počet vzpěračů) statisticky menší, u nejtěžších vah má vliv tělesný tuk, který u středních kategorií neexistuje. Tento závěr potvrzuje i mocninná aproximace závislosti rekordu na hmotnosti. I zde je exponent menší, nežli očekávané 2/3, protože nejtěžší kategorie mají relativně nižší výkony. To platí i v říši zvířat: zatím co mravenec zvedne mnohonásobek své hmotnosti, slon jen zlomek. I tento jev souvisí s mocninnou závislostí
kterou jako první popsal Lietzke.
Literatura:
- Lietzke T. H.: Science 124, 1956, č. 3220
G09 Výdej energie při kolísavé rychlosti v lokomočních sportech
V lokomočních sportech (běh, chůze, plavání, lyžování, rychlobruslení, cyklistika, vodní sporty) je výsledkem čas T pro danou trať L, závisející na průměrné rychlosti v
Zvyšování rychlosti brání kromě vnitřních sil v těle také odpor prostředí, rostoucí s druhou mocninou rychlosti
Práce pro celý závod o délce L je pak
Jestliže na příklad plavec z závodě na 100 m za 50 s uplave obě půlky stejně rychle (25 + 25 s) nebo s rostoucím rozdílem, musí při tom vykonat práci, úměrnou výrazu
| t1+t2(s) | A | účinnost % |
|---|---|---|
| 25+25 | 400 | 100 |
| 24+26 | 401,925 | 99,5 |
| 23+27 | 407,76 | 98,1 |
| 22+28 | 417,7 | 95,8 |
Z tabulky vyplývá pravidlo:
Čím větší jsou změny rychlosti, tím větší je výdej energie a tím nižší je účinnost lokomoce.
Důvodem je nelineární závislost odporu prostředí na rychlosti, která má za následek zvětšení výdeje při zvýšení rychlosti větší nežli je snížení výdeje při poklesu rychlosti.
Kolísání rychlosti během každého cyklu lokomoce (kroku, tempa, záběru vesla či pádla) bývá často mnohem větší nežli mezi jednotlivými úseky závodu. Změříme-li tachografem průběh okamžité rychlosti, můžeme vyvzorkovat časově ekvidistantní rychlosti a pomocí nich vypočítat výdej energie při této kolísavé rychlosti.
Výkon N při okamžité rychlosti vi je
Element práce
a pro celý cyklus, trvající dobu T je to součet
Účinnost je pak poměr práce při rovnoměrné rychlosti a nerovnoměrné rychlosti
kde n = T / dt je počet vzorků okamžité rychlosti vi.
americký znakař Templeton s nejlepším výkonem na 100 m 57,60 s (1976) zaplaval na tachografu 11.12.1976 trať 100 m za 1:01,4 s následujícím průběhem okamžité rychlosti:
| t(s) | v(m/s) |
|---|---|
| 0,0 | 1,2 |
| 0,05 | 1,4 |
| 0,10 | 1,65 |
| 0,15 | 1,85 |
| 0,20 | 1,88 |
| 0,25 | 1,85 |
| 0,30 | 1,86 |
| 0,35 | 1,84 |
| 0,40 | 1,72 |
| 0,45 | 1,57 |
| 0,50 | 1,53 |
| 0,55 | 1,54 |
| 0,60 | 1,52 |
| 0,65 | 1,45 |
| 0,70 | 1,36 |
účinnost e = 15 · 1,614733 / 66,204 = = 0,9536 = 95,36 %
Všechny potřebné sumace a výpočty provedeme snadno a rychle programem:
DATA 1.2,1.4,1.65,1.85,1.88,1.85,1.86,1.84,1.72,1.57,1.53
DATA 1.54,1.52,1.45,1.36
a:
READ v: ON ERROR GOTO b
s=s+v:k=k+v*v*v
n=n+1:GOTO a
b:
vs=s/n
e=n*vs^3/k
PRINT "prům.rychlost,účinnost=";vs,e
END
prům. rychlost, účinnost = 1,614, 0,9534
Fakulta sportovních studií, Masarykova univerzita |
Návrat na úvodní stránku webu, přístupnost |
| Servisní středisko pro e-learning na MU
| Fakulta informatiky Masarykovy univerzity, 2011
Technické řešení této výukové pomůcky je spolufinancováno Evropským sociálním fondem a státním rozpočtem České republiky.

