Sport, matematika, počítač
Fakulta sportovních studií Masarykovy univerzity
Ing. Josef Kopřiva

Kliknutím na šedou plochu pod nápisem se vrátíte zpět nahoru

H. Sporty obecně

Část H01–H06

H01 Kvalita a četnost sportovních výkonů

V disciplinách se světovými rekordy rozlišujeme dva případy:

discipliny s maximálními výsledky jako rekordy (skoky, vrhy a hody, vzpírání, hodinovky a jiné časově omezené lokomoce)
disciplíny s minimálními časy jako rekordy (běhy, plavání, rychlobruslení, cyklistika)

Rekord je jediný, a s klesající hodnotou výkonů poroste jeho četnost, tj. počet sportovců, kteří výkon dosahují. To vyjádří dva grafy:

Obr. H01ab: Rekord je jediný, a s klesající hodnotou výkonů
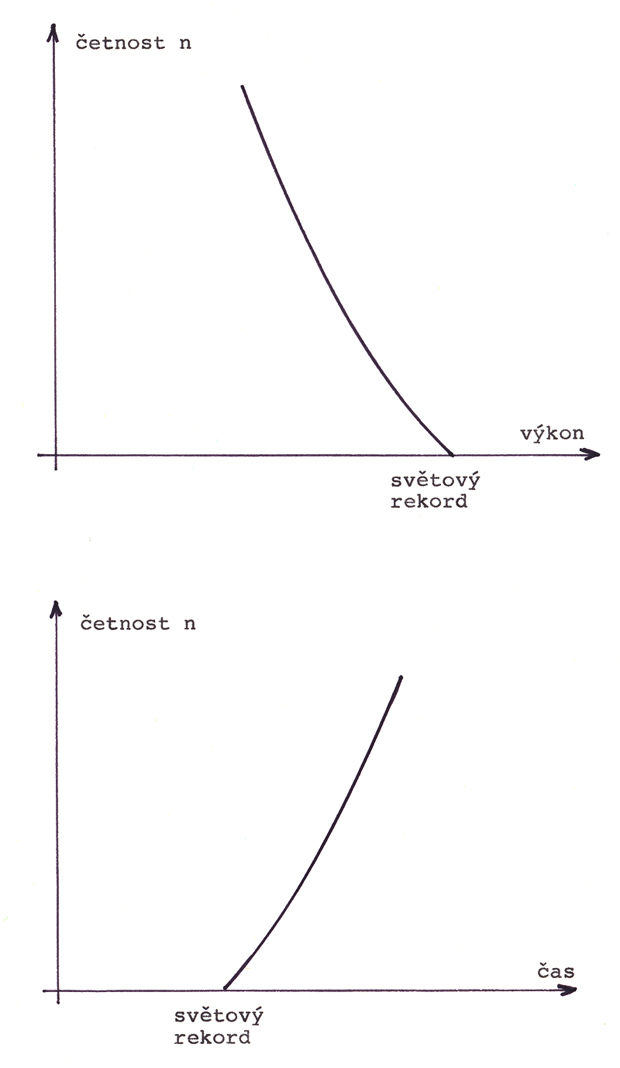
poroste jeho četnost, tj. počet sportovců, kteří výkon dosahují.

Inversní závislost výsledku na jeho četnosti je na obr. H01c

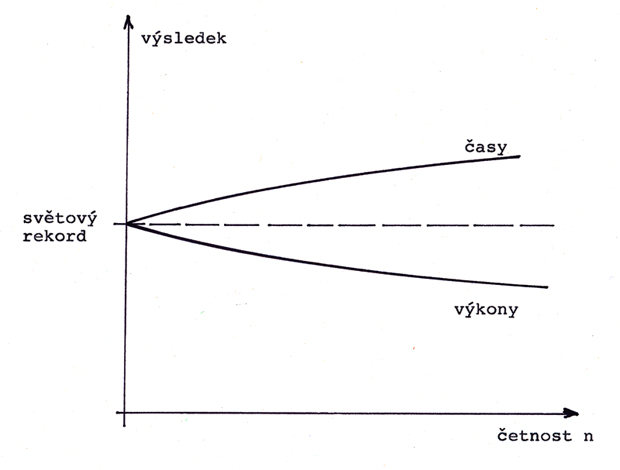
Obr. H01c: Inversní závislost výsledku na jeho četnosti

Takový model popsali Karvonen a Kihlberg (literatura 66, 67), a odpovídá mu mocninná funkce jako model Parettova rozdělení

$p=a.n^b$

kde

a … součinitel, blízký světovému rekordu

b … exponent blízký nule, kladný pro časy, záporný pro rostoucí výkony

n … četnost sportovců

p … výsledek (výkon)

Činitele a, b lze vypočítat metodou nejmenších čtverců, což jsme provedli pomocí světového rekordu a několika výkonů, jejichž četnost jsme zjistili pomocí tabulek lehkoatletických výkonů v roce 1989. Dostali jsme tyto výsledky:

běhy	muži	ženy
100m	9,94 · n^0.00897	10,74 · n^0.014605
200m	19,96 · n^0.009473	22,04 · n^0.013836
400m	44,27 · n^0.009312	50,01 · n^0.01183
800m	103,16 · n^0.0082404	114,4 · n^0.01513
1500m	210,55 · n^0.009415	239,23 · n^0.012444
1 míle	229,9 · n^0.010308	255,61 · n^0.02398
3 km	449,45 · n^0.01106	518,48 · n^0.01115
5 km	784,24 · n^0.00878	899,01 · n^0.01638
10 km	1628,23 · n^0.01259	1848,51 · n^0.017528
maratón	7681,0 · n^0.009297	8673,0 · n^0.018033
110m př.	12,92 · n^0.016344	12,60 · n^0.0145
400m př.	47,86 · n^0,011874	53,73 · n^0.01728
3km př.	485,35 · n^0.013634
skok vysoký	244 · n^-0.01954	204 · n^-0.018894
skok daleký	870 · n^-0.020946	730 · n^-0.02688
trojskok	17,65 · n^-0.01397	14,52 · n^-0.03246
skok o tyči	603 · n^-0.019977
koule	22,66 · n^-0.038835	20,78 · n^-0.05279
disk	70,92 · n^-0.035875	75,56 · n^-0.05984
oštěp	87,60 · n^-0.028854	76,88 · n^-0.065733
kladivo	82,84 · n^-0.03142
desetiboj	8549 · n^-0.02707	sedmiboj: 7007 · n^-0.045
20km chůze	4734 · n^-0.01557	5km 1225 · n^-0.02495
50km chůze	13061 · n^-0.0289	0km 2536 · n^-0.023435
4x100m	38,23 · n^0.008357	41,87 · n^0.014494
4x400m	180,99 · n^0.00731	203,05 · n^0.013375

Pozn.: vzorce pro časy platí pro sekundy! V roce 1990 nebyly ještě běžné ženská tyč, kladivo a 3 km přek.

Souhrnně lze říci, že čím větší absolutní hodnota exponentu, tím rychleji klesá hodnota výkonu s četností výkonu. Nejrychlejší pokles je u ženských vrhů a hodů.

Literatura:

Kihlberg J. – Karvonen M. J. Comparison on statistical basis of achievement in track and field events. Reseach Quarterly, 28, 1957, 3, 244–256
Kihlberg J. – Karvonen M. J.: Statistical distribution and predictability of top class achievements in track and field sporting events. Wychowanie Fyziczne i Sport, 4, 1960, 145–56
Světové tabulky 1989, Praha, ASTAT, 1990

Nahoru

H02 Křivka světových rekordů

Někdy můžeme potřebovat světový rekord v lokomočních sportech na neobvyklé trati. Vypočítat jej ze známých světových rekordů můžeme pomocí aproximační funkce. Osvědčila se aproximace polynomem stupně o 1 nižším, nežli je počet vložených rekordů. Součinitele pro polynom typu

$t=a_n.L^n+a_{n-1}.L^{n-1}+…+a_1.L+a_0$

vypočítáme metodou nejmenších čtverců, uvedenou v kap. C05.

Pod tabulkami rekordů jsou uvedeny získané polynomy v Hornerově tvaru:

Atletické rekordy v běhu ke dni 1. 6. 2003

trať (m)	muži	ženy
400	43,18	47,60
800	101,11	113,28
1500	206	230,46
5000	759,36	868,09
10000	1582,75	1771,78

muži: t = (((0,045261 · L – 0,9127) · L + 6,7922) · L + 137,653) · L – 12,91

ženy: t = (((-0,0557106 · L + 0,56279) · L + 1,67246) · L + 161,62) · L – 17,35

Plavecké rekordy ke dni 1. 6. 2003

trať (m)	muži	ženy
100	47,84	53,77
200	104,06	116,64
400	220,08	243,85
800	459,16	496,22
1500	877,48	952,10

muži: t = (((0,00150656 · L – 0,06592) · L + 1,00526) · L + 53,63) · L – 6.74

ženy: t = (((0,004857 · L) – 0,12006) · L + 0,9155) · L + 60,891) · L – 7,92

Rychlobruslařské rekordy ke dni 1. 6. 2003

trať (m)	muži	ženy
500	34,32	37,29
1000	67,18	74,06
1500	103,95	114,02
3000	222,75	237,70
5000	374,66	406,91
10000	778,92

Muži: t = ((((-0.01062 · L + 0,343936) · L – 3,77254) · L + 17,052) · L + 46,154) · L + 7,433

Ženy: t = (((0,411035 · L – 4,5114) · L + 17,345) · L + 54,647) · L + 6,168

Cyklistické světové rekordy k 1. 6. 2003

trať (km)	muži	ženy
1	58,875	73,377
3		210,764
4	251,114
10	647,102	731,99
44,767		3600
49,441	3600

Muži: t = ((-0,000370372 · L + 0,21871) · L + 62,994) · L – 4,337

Ženy: t = ((-0,0010248 · L + 0,7843) · L + 65,69) · L + 6,9135

Pozn.: uvedené polynomy nepoužíváme mimo rozsah tratí, které byly vloženy. Rekordy byly postiženy zrušením výkonů na speciálních kolech. Přehled jiných aproximačních funkcí uvádí kniha

Literatura:

Zaciorskij V. M. Kibernetika, matěmatika, sport. Moskva, FiS, 1969, str. 94–95

Nahoru

H03 Relativní výkonnost žen vůči mužům podle světových rekordů (podle stavu k 15. 8. 2005)

Ženy dosahují nižších výkonů nežli muži z mnoha důvodů, mezi nimiž hlavní jsou menší průřez svalů, jiná stavba těla a hormonální funkce. Nejjednodušší srovnání dává poměr světových rekordů. U výkonů, rostoucích s číselným výsledkem (např. skok vysoký) použijeme poměr

$r=\frac{rekord\hspace{1 mm}žen}{rekord\hspace{1 mm}mužů}×100\hspace{1 mm}(\%)$

u výkonů, klesajících s rostoucím číselným výsledkem (např. běh na 100 m) naopak

$r=\frac{rekord\hspace{1 mm}mužů}{rekord\hspace{1 mm}žen}×100\hspace{1 mm}(\%)$

Teoretický přepočet na jiné kriterium (fysiologický výdej, mechanický výkon nebo práce) by musel být dobře zdůvodněn, aby nebyl subjektivní.

Z poměrů pro jednotlivé rekordy lze vypočítat průměry pro jednotlivé sporty, které tvoří následující pořadí:

1. rychlobruslení	r = 91,67 %	(n = 6 tratí)
2. plavání	r = 90,01 %	(n = 17 disciplin)
3. atletika	r = 88,66 %	(n = 20 disciplin)
4. cyklistika	r = 87,82 %	(n = 9 tratí)
celkem všechny sporty	88,52 %	(n = 52 disciplín)

Vzpírání není možné porovnat pro rozdíly váhových kategorií

Jednotlivé discipliny, trati nebo váhové kategorie ukazují následující tabulky:

1. rychlobruslení

500 m	34,22 / 37,29	92,0 %
1000 m	1:07,18 / 1:14,06	90,7 %
1500 m	1:46,43 / 1:58,95	91,0 %
3000 m	3:43,95 / 3:57,50	!max! 94,7 %
5000 m	6:14,66 / 6:46,91	92,1 %
10000 m	12:58,92 / 14:22,6	90,3 %
celkem		91,67 %

2. plavání

50 m kr	21,64 / 24,13	89,7 %
100 m kr	47,84 / 53,52	89,4 %
200 m kr	1:44,06 / 1:56,64	89,2 %
400 m kr	3:40,08 / 4:03,85	90,3 %
800 m kr	7:38,65 / 8:16,22	92,4 %
1500 m kr	14:37,89 / 15:52,10	92,2 %
		kraul 90,53 %
50 m df	22,96 / 25,57	89,8 %
100 m df	50,40 / 56,61	89,0 %
200 m df	1:55,22 / 2:05,96	90,7 %
		delfín 89,83 %
50 m zn	24,80 / 28,19	(88,0 %)
100 m zn	53,17 / 59,58	89,2 %
200 m zn	1:54,66 / 2:06,62	90,6 %
		znak 89,27 %
50 m pr	27,18 / 30,57	88,8 %
100 m pr	59,30 / 1:06,20	89,6 %
200 m pr	2:09,04 / 2:21,72	91,1 %
		prsa 90,1 %
100 m pol	53,10 / 1:00,6	87,6 %
200 m pol	1:55,94 / 2:09,72	89,4 %
400 m pol	4:08,26 / 4:33,59	90,7 %
		polohový 90,05 %
celkem		90,01 %

3. atletika

běhy:	60 m	6,39 / 6,92	92,3 %
	100 m	9,77 / 10,49	!max! 93,1 %
	200 m	19,32 / 21,34	90,5 %
	400 m	43,18 / 47,60	90,7 %
	800 m	1:41,11 / 1:53,28	89,3 %
	1000 m	2:11,96 / 2:28,98	88,6 %
	1500 m	3:26,00 / 3:50,46	89,4 %
	2000 m	4:44,79 / 5:25,36	87,5 %
	3000 m	7:20,64 / 8:06,13	90,6 %
	5000 m	12:37,35 / 14:24,68	87,6 %
	10000 m	26:20,31 / 29:31,78	89,2 %
	Hodina	21,101 km/ 18,340 km	86,1 %
	Maratón	2:04:55 / 2:15:25	92,2 %
			běhy 89,80 %
skoky:	vysoký	245 / 209	85,3 %
	daleký	895 / 752	84,0 %
	trojskok	18,29 / 15,50	84,9 %
	tyč	615 / 501	81,5 %
			skoky 84,70 %
vrhy, hody a překážkové běhy nelze srovnávat

	chůze: 5 km	18:07,08 / 20:02,60	90,4 %
	10 km	38:02,60 / 41:04,0	82,9 %
	20 km	1:17:21 / 1:35:41	90,3 %
			chůze 87,87 %
	celkem		88,49 %

4. cyklistika

200m let	9,865 / 10,831	91,1 %
500m let	26,325 / 29,655	88,8 %
1000m let	57,224 / 1:05,232	87,7 %
1 km pev	58,875 / 1:13,377	80,2 %
5 km pev	5:27,039 / 6:05,198	89,6 %
10 km	10:47,102 / 12:11,99	88,4 %
20 km	21:23,932 / 24:55,028	85,9 %
Hodina	49,700 km/ 44,767 km	90,1 %
100 km	2:10:08,29 / 2:28:26,26	87,7 %
celkem		87,72 %

Desítka nejlepších žen:

1. Niemannová	3 km rychlobruslení	94,7 %
2. Griffithová	100 m běh	93,1 %
3. Evansová	800 m kraul	92,4 %
4. Privalova	60 m běh	92,3 %
5. Redcliffe	maratón	92,2 %
6. Le Doan	500 m rychlobruslení	92,0 %
7. Jones	200 m prsa	91,1 %
8. Wittyová	1000 m rychlobruslení	90,7 %
9. Egerszegyi	200 m znak	90,7 %
10. Kločková	400 m polohový závod	90,7 %

V první desítce jsou 3 rychlobruslařky, 4 plavkyně a 3 atletky

Resumé:

Sporty, v nichž se ženy nejvíce blíží mužským výkonům jsou rychlobruslení, plavání a cyklistika (91–téměř 94 %)
Nejméně se blíží ženy mužům ve vzpírání (65–73 %). Ženy nemají předpoklady pro silové sporty.
V bězích klesá relativní výkonnost žen s délkou trati (Redcliffová je výjimka), v plavání je tomu naopak. Plavání je výhodné pro vytrvalost dík vodnímu prostředí.
Srovnání bylo provedeno jen ve sportech s měřenými výsledky, v jiných sportech nelze podobné objektivní srovnání provést.

Nahoru

H04 Charakteristické rovnice vybraných sportovních disciplin

V mnoha sportovních disciplinách je možno nalézt matematické vztahy mezi výsledkem sportovce a několika hlavními činiteli, určujícími tento výsledek. Tyto rovnice, někdy jen symbolické můžeme nazvat charakteristickými, a v následujícím textu uvedeme některé příklady.

sprinterské běhy. Výsledný čas má tři části:
$t=t_r+t_z+t_v=t_r+\sqrt{2\frac{s}{a}}+\frac{L_v}{f_k.L_k}$
t_r … reakční doba na startu, kterou nelze podstatně zkrátit
t_z … doba zrychlování, závisí na zrychlování a proto na výbušné svalové síle nohou
t_v … doba běhu poměrně stálou rychlostí, závisí na součinu délky kroku L_k
a frekvence kroků f_k

Sprinter může zkrátit svůj čas, jestliže
1. zkrátí svou reakční dobu
2. zvýší výbušnou svalovou sílu nohou
3. prodlouží délku kroku nebo zvýší frekvenci kroků, nejlépe obojí současně
4. zvýší sprinterskou vytrvalost a udrží tak rychlost déle
střední a dlouhé běžecké tratě jsou problémem omezených fysiologických zdrojů energie a vytrvalosti. Běžec musí
1. urychlit na střední rychlost běhu a proto vykonat práci, úměrnou kinetické energii
  $E=\frac{1}{2}m.v_s^2$
2. překonávat odpor vzduchu F_o prací
  $A_o=k.v_s^2.L$
3. vykonat práci na zvedání těžiště těla při každém kroku
  $A_z=n.m.g.\Delta{H}$
  n … počet kroků
  m … hmotnost těla
  g … gravitační zrychlení
  ∆H … zvednutí těžiště při každém kroku
4. vykonat práci na zvedání těžiště při běhu v zatáčce (viz L06)
5. vykonat práci, spojenou se zrychlováním
  
  Běžec na středních a dlouhých tratích musí
  1. být štíhlý, aby zmenšil práci v gravitačním poli
  2. optimalizovat délku a frekvenci kroku
  3. udržovat stálou rychlost, aby zmenšil ztráty zrychlováním
skoky vysoký. Maximální výška laťky, kterou skokan překoná, je součet tří výšek: výšky těžiště těla nad zemí v odrazové poloze, zdvihu těžiště impulsem odrazové síly, a rozdílu mezi výškou laťky a těžiště v nejvyšším bodě
$H=H_t+H_{odr}+\Delta{H_l}$
Skokan do výšky dosáhne velké výšky, jestliže bude mít
1. vysoko těžiště těla, tedy dlouhé nohy
2. nízkou hmotnost těla (štíhlost), aby lépe využil výbušné síly a impulsu této síly
3. dokonalou techniku přechodu nad laťkou
Podrobnější analýza by ukázala význam dalších činitelů (anatomie těla a odrazové nohy, orientace v prostoru při flopu, optimální rychlost rozběhu atd.)
skok o tyči. Zde skočená výška je součtem pěti výšek:
1. výšky těžiště těla při odrazu
2. zdvihu těžiště těla svislým odrazem
3. zdvihu tyčí, který závisí na rychlosti rozběhu a technice
4. zdvihu pažemi před puštěním tyče
5. rozdílu mezi laťkou a obrysem těla
Skokan o tyči musí mít vysoko těžiště těla, velkou svislou odrazovou sílu, co největší rychlost rozběhu a tím i kinetickou energii, kterou uloží do ohýbající se laminátové tyče, laminátovou tyč vysoké pružnosti, aby využil uloženou energii ke stoupání, velkou sílu paží při odrazu od tyče, a dokonalou techniku přechodu přes laťku.
vrhy a hody. Platí jednoduché pravidlo: největší vzdálenosti dosáhne vrhač maximální možnou počáteční rychlostí a optimálním počátečním úhlem dráhy náčiní. Pro parabolickou dráhu je optimální úhel (podle G02)

$\alpha_{opt}=\frac{1}{2}\arctan{(\frac{L}{H_0})}$
L … vodorovná délka vrhu
H … počáteční výška dráhy

U parabolických vrhů (koulí) bude výsledek nejlepší, bude-li mít vrhač maximální výbušnou sílu a optimální počáteční úhel dráhy, vždy menší nežli 45°, u ostatních vrhů s balistickou drahou (vlivem odporu vzduchu) musí vrhač natrénovat optimální počáteční úhel, jiný nežli u parabolické dráhy. Zkušenost a technika se silou je nepostradatelná.
Plavání a veslování mají společný odpor vody a setrvačnost, takže sportovec musí překonávat součet těchto dvou sil. Většinou bývá setrvačná síla, kterou je nutno překonávat větší, nežli odpor vody:
$F=F_o+F_s=k.v^2+m.a$
Zrychlení a zpoždění během každého tempa jsou závislé prakticky jen na plavecké technice, tj. provedení záběrových a přípravných pohybů, odpor vody a tedy i zpožďování závisí hlavně na poloze těla.

Úspěšný plavec musí zvládnout dva hlavní problémy své plavecké techniky: polohu těla s nejmenším možným odporem vody, a záběrové pohyby s maximální a maximálně rovnoměrnou silou a výslednou rychlostí.

Nahoru

H05 Vliv startu v lokomočních sportech

Ve většině lokomočních sportů začíná závod pevným startem (z klidu), výjimkou jsou jen cyklistické sprinty letmo. U dlouhých tratí má start zanedbatelný vliv na celkový výsledek a proto se zde omezíme jen na krátké závody.

Podle vlivu startu na průběh okamžité rychlosti sportovce musíme rozlišovat

sporty, u nichž start a následující zrychlování je pomalejší, než zbytek závodu. Sem patří běh, cyklistika, rychlobruslení, lodní sporty apod.
sporty, u nichž start a bezprostředně následující část závodu je rychlejší, nežli zbytek závodu. Sem patří plavání se startovním skokem.

Obr. H05 ukazuje graficky rozdíl mezi těmito dvěma skupinami.

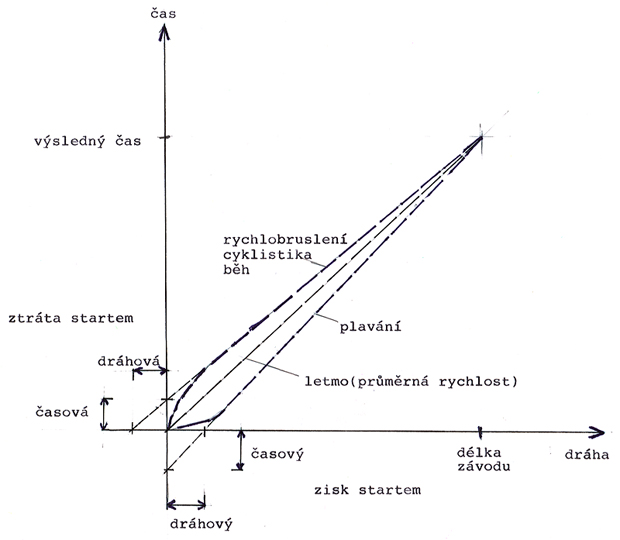
Obr. E01: Průběh okamžité srdeční frekvence

Obr. H05: Grafické zobrazení rozdílu dvou daných skupin sportů

Vynecháme-li startovní reakční dobu, můžeme přibližně lineární částí grafu proložit dvě regresní přímky:

$L=v_1.t-L_1\hspace{20 mm}t=\frac{L}{v_1+t_1}$

$L=v_2.t+L_2\hspace{20 mm}t=\frac{L}{v_2-t_2}$

kde

L₁ … ztráta dráhy startem

L₂ … zisk dráhy startem

t₁ … ztráta času startem

t₂ … zisk času startem

Příklad:

Carl Lewis měl na OH 1988 v Soulu na 100 m za 9,92 s následující mezičasy, časy úseků a rychlosti podle tabulky:

L(m)	t(s)	Δt(s)	v(m/s)
10	1,89	1,89	5,29
20	2,96	1,07	9,35
30	3,90	0,94	10,54
40	4,79	0,89	11,23
50	5,65	0,86	11,63
60	6,48	0,83	12,05
70	7,33	0,85	11,76
80	8,18	0,85	11,76
90	9,04	0,86	11,63
100	9,92	0,88	11,36

Z tabulky plyne, že rozběh byl další než 40 m. Proložíme-li úseky a časy od 50 do 100 m regresní přímku, dostaneme

L = 11,3943 · t – 13,53 (s)
t = L / 11,4045 + 1,1913 (m)

Pozn.: regresní činitelé nejsou navzájem převratné hodnoty, protože součinitel korelace není 1 (0,99955).

Ztratil tedy Lewis startem 1,19 s, což dává při průměrné rychlosti ztrátu dráhovou 13,53 m. Pro některé vrcholové sprintery dostaneme:

jméno	čas	čas regresně	dráha regresně
Lewis C.	9,92	t = 0,087685 · L + 1,1913	L = 11,3943 · t – 13,53
Christie L.	9,97	t = 0,086 · L + 1,355	L = 11,6272 · t – 15,75
Smith C.	9,99	t = 0,0866 · L + 1,312	L = 11,54 · t – 15,138
Ženy:
Griffith-Joyner	10,54	t = 0,0916 · L + 1,383	L = 10,9169 · t – 5,097
Ashford E.	10,85	t = 0,0956 · L + 1,283	L = 10,46 · t – 13,42

S těmito údaji můžeme srovnávat kvalitu startu a rozběhu. Plavání se na rozdíl od ostatních sportů vyznačuje vyšší rychlostí po startovním skoku nežli ve zbývající části závodu: ve vzduchu letí plavec po odskoku vodorovnou rychlostí 4–6 m/s, zatím co rychlost plavání bývá pod 2 m/s.

Příklad:

brazilská štafeta 4x100m kraul na mistrovství světa v krátkém bazéně v prosinci 1995 v Rio de Janeiro zaplavala mezičasy, z nichž můžeme vypočítat lineární regresní rovnice:

jméno	čas	čas regresně	délka regresně
Scherer	47,63	t = 0,4825 · L – 0,74	L = 2,07185 · t + 1,538
Masura	48,16	t = 0,4984 · L – 1,85	L = 2,00579 · t + 2,006
Cordera	49,16	t = 0,51304 · L – 2,205	L = 1,94894 · t + $,305
Borges	47,47	t = 0,4912 · L – 1,725	L = 2,0359 · t + 3,5146

U prvního člena štafety se projevuje vliv reakční doby na startu, který z velké části odpadá u dalších, protože mohou startovat podle dohmatu předchozího, tedy s návěštím. Také zde nám absolutní členy rovnic vypovídají o kvalitě startu.

Nahoru

H06 Maximální rychlosti v lokomočních sportech

Maximální rychlosti mužů a žen v lokomočních sportech (ke dni 1.1.2001)

	muži				ženy
trať	čas	v (m/s)	v (km/h)	v (mph)	čas	v (m/s)	v (km/h)	v (mph)	r (%)
lyžování
1 km letmo	14,510	68,92	248,105	154,17	15,35	65,15	234,528	145,73	94,5
cyklistika
200m letmo	9,865	20,27	72,985	45,35	10,83	18,47	66,476	41,306	91,1
l km pev.	1:00,148	16,626	59,852	37,19	1:13,38	13,63	49,06	30,484	82,0
10 km	10:47,102	15,454	55,633	34,539	12:11,99	13,66	49,18	30,56	88,4
56,376 km	1 hour	15,66	56,37	35,03	1 hour	13,378	48,159	29,925	85,4
rychlobruslení
500m	34,76	14,38	51,78	32,18	37,40	13,37	48,13	29,91	92,9
1500 m	1:46,43	14,09	50,74	31,53	1:55,50	12,99	46,75	29,05	92,1
5000 m	6:18,72	13,20	47,53	29,53	6:55,34	12,04	43,34	26,93	91,2
10000 m	13:03,40	12,76	45,95	28,55	14:22,6	11,59	41,73	25,93	90,8
běh
100 m	9,79	10,21	36,77	22,85	10,49	9,53	34,32	21,32	93,3
200 m	19,32	10,352	37,267	23,157	21,34	9,37	33,74	20,96	90,5
800 m	1:41,11	7,912	28,484	17,70	1:53,26	7,06	25,43	15,80	89,3
1500 m	3:26,00	7,28	26,214	16,289	3:50,46	6,51	23,43	14,56	89,4
5000 m	12:39,36	6,58	23,70	14,73	14:28,09	5,76	20,73	12,88	87,5
10000 m	26:22,75	6,318	22,745	14,133	29:31,78	5,64	20,32	12,62	89,3
42195 m	2:05:42	5,59	20,14	12,51	2:20:47	4,99	17,98	11,17	89,6
veslování
2 km skif	6:38,97	5,013	18,046	11,216	7:17,09	4,567	16,473	10,23	91,3
2 km osma	5:18,8	6,274	22,585	14,034	5:59,26	5,567	20,04	12,45	88,7
plavání
50 m	21,64	2,31	8,32	5,17	24,13	2,07	7,46	4,63	89,7
100 m	47,84	2,09	7,53	4,68	53,77	1,86	6,69	4,16	89,0
400 m	3:40,59	1,81	6,53	4,05	4:03,85	1,64	5,91	3,67	90,5
1500 m	14:41,66	1,70	6,125	3,81	15:52,1	1,57	5,67	3,52	92,6

autor: Ing. Josef Kopřiva, recenzent: Mgr. Martin Sebera, Ph.D. |
Fakulta sportovních studií, Masarykova univerzita |
Návrat na úvodní stránku webu, přístupnost |

| Technická spolupráce:
| Servisní středisko pro e-learning na MU
| Fakulta informatiky Masarykovy univerzity, 2011

Technické řešení této výukové pomůcky je spolufinancováno Evropským sociálním fondem a státním rozpočtem České republiky.

Nahoru

INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ