H. Sporty obecně
Část H07–H12
H07 Zpracování mezičasů
V běhu, plavání, cyklistice, rychlobruslení a jiných sportech se měří mezičasy pro úseky stejné délky (kola, bazény, 100 m nebo 1 km). Protože rovnoměrná rychlost je velmi důležitá pro dosažení nejlepšího výkonu, můžeme ji kontrolovat pomocí
- nejlepšího, průměrného a nejhoršího času úseku
- výpočtem variačního součinitele časů úseků v %
Potřebné výpočty a operace provede následující program
DATA.553,1.5364,2.5261,3.5159,4.5059,5.4967,6.49,7.4827,8.4743
DATA 9.4691,10.4628,11.4586,12.4623,13.4597,14.4348
INPUT "jmeno,datum "; j$, d$
INPUT "trat(m), cas(m.s),počet mezicasu "; l, t, n
CLS: PRINT j$, d$, l, t: PRINT
mi = 1000000!: p = ma = 0: l1 = l / n
FOR i = 1 TO n: READ t
s = 60 * INT(t) + 100 * (t – INT(t))
d = s – p: a = a + d: k = k + d * d
g = g + 1 / (d * d): r = l1 / d
IF d < mi THEN LET mi = d
IF d > ma THEN LET ma = d
p = s: PRINT t, s, d, r: NEXT i: PRINT
m = a / n: sx = SQR((k – a * a / n) / (n – 1))
v = sx * 100 / m: e = n * n * n / (a * a) / g
PRINT "min,prum,max,sx "; mi, m, ma, sx
PRINT "var.koef.,ucinnost "; v; "%";, e
END
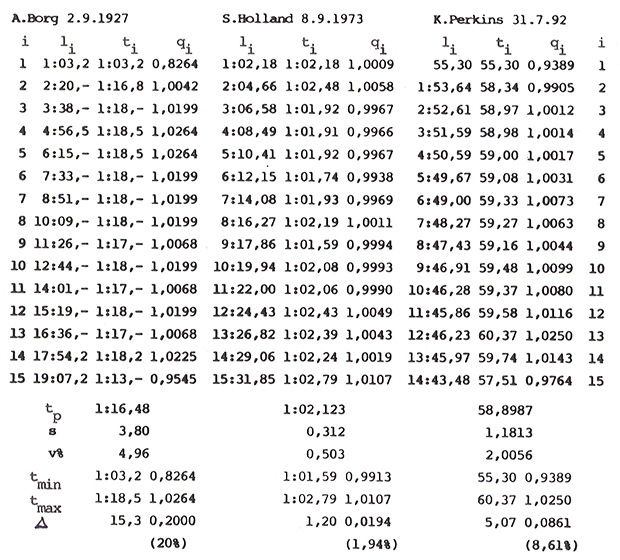
z mezičasů světového rekordu na 1500 m kraul muži (K. Perkins) v prvních řádcích programu dostaneme:
| 1 | 55.30 |
| 2 | 58.34 |
| 3 | 58.97 |
| 4 | 58.98 |
| 5 | 59.00 |
| 6 | 59.08 |
| 7 | 59.33 |
| 8 | 59.27 |
| 9 | 59.16 |
| 10 | 59.48 |
| 11 | 59.37 |
| 12 | 59.58 |
| 13 | 60.37 |
| 14 | 59.74 |
| 15 | 57.51 |
| min | 55.3 |
| průměr | 58.852 |
| max | 60.37 |
| var % | 3.13 |
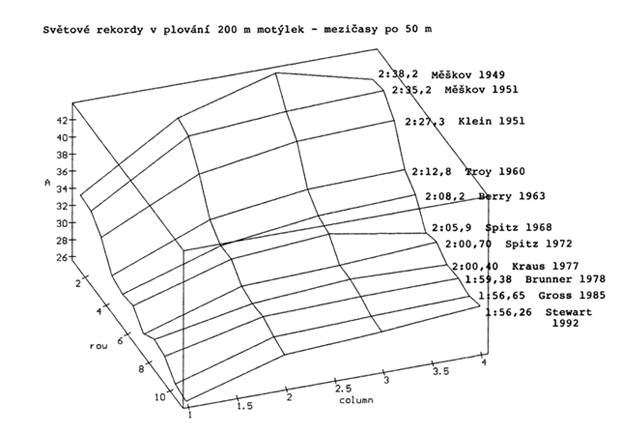
Chceme-li názorně porovnat mezičasy z několika závodů, např. světových rekordů, použijeme k tomu trojrozměrný graf, který je schopen vytvořit systém MAPLE V. Postupujeme takto:
- do programu vepíšeme časy úseků, vypočítané jako v předešlém příkladu, jako jednotlivé vektory vi
- z vektorů vytvoříme matici dat
- matici dat necháme nakreslit jako trojrozměrný graf na monitoru
- kurzorovými klávesami můžeme graf naklápět a natáčet, až je nejnázornější
- nakonec graf vytiskneme
- mezičasy světových rekordmanů na 200 m motýl muži, kde jsou uvedeny i příkazy MAPLE V a výsledný graf
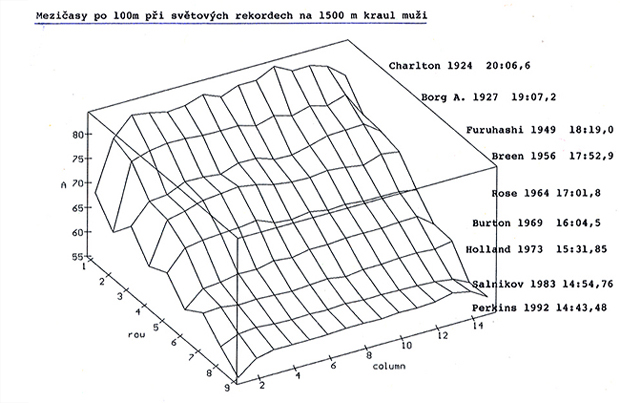
- mezičasy na 1500 m kraul muži s výpočtem časů úseků a jejich poměru qi k průměrnému času úseku a výsledný graf. Tyto poměrné součinitele lze použít k výpočtu analogických časů pro jiný výsledný a tedy i průměrný čas.

H08 Kvantitativní kriterium vytrvalosti
Vytrvalost je definována jako schopnost pracovat intensivně po dlouhou dobu vzdor únavě. Je to tedy kombinovaná vlastnost fyziologicko – psychologická.
Stroj (automobil, motorový člun, letadlo, …) může udržovat svou rychlost po dlouhou dobu, protože únava nehraje žádnou roli.
Člověk jako fyziologický "stroj" musí překonávat únavu, která roste s intensitou a trváním zátěže. Žádný sportovec není schopen udržet vysokou rychlost po neomezenou dobu, a časy pro delší trati porostou rychleji, nežli délka trati.
Na příklad světový rekordman etiopský běžec Haile Gebreselasie dosáhl těchto nejlepších časů:
| trať | čas | čas | rychlost |
|---|---|---|---|
| (km) | (m:s) | (s) | (m/s) |
| 0,8 | 1:50,39 | 110,39 | 7,25 |
| 1,5 | 3:31,76 | 211,76 | 7,08 |
| 2 | 4:52,86 | 292,86 | 6,83 |
| 3 | 7:25,09 | 445,09 | 6,74 |
| 5 | 12:39,36 | 759,36 | 6,58 |
| 10 | 26:22,75 | 1582,75 | 6,32 |
Jeho aproximační funkce, vhodná pro vztah mezi délkou trati a časem v sekundách se ukázala
Vypočítáme-li metodou nejmenších čtverců čas t1 pro jednotkovou trať 1 km a exponent n, dostaneme pro Gebreselasieho vztah
a součinitel korelace této funkce s tabulkou bude r = 0,999974. Součinitel t1 je čas na 1 km v sekundách, tedy 2:19,54 v minutách a sekundách. To je vynikající ukazatel rychlosti tohoto vytrvalce.
Exponent n = 1,05469 ukazuje, jak rychle se zhoršují časy s délkou trati, a je to tedy ukazatel vytrvalosti. U stroje by bylo n = 1, u sportovců jsme vyhodnocením velkého množství běžců, plavců, cyklistů a rychlobruslařů nalezli tyto hodnoty:
| n | vytrvalost |
|---|---|
| 1 – 1,04 | velmi vysoká |
| 1,05-1,1 | vysoká |
| 1,2 -1,4 | střední |
| 1,5 -1,8 | nízká |
| 1,9 a více | velmi nízká |
Nejvyšší vytrvalost, tedy nejnižší hodnotu exponentu n jsme nalezli v plavání u australského světového rekordmana Stephena Hollanda – n = 1,013. Vysvětlení podává fysiologie práce:
v plavání je lidské tělo vodou chlazený "stroj" a může se snadno zbavovat odpadového tepla, což jiné sporty nedovolují.
V cyklistice, kde závodník dosahuje velmi vysokých rychlostí po podstatně delším zrychlování nežli v jiných sportech, má exponent někdy překvapivě nízkou hodnotu, a také u rychlobruslení jsou časy ne 1 km často lepší, nežli dvojnásobek času na 500m. Musíme tedy exponent interpretovat opatrně a hlavně srovnávat s jinými případy. Program pro výpočet t1, n pomocí aproximace mocninnou funkcí následuje.
Literatura
- Kopřiva J. Kvantitativní měřítko vytrvalosti. Teor. praxe. těl.vých., 35, 1987, č. 5, str. 271–274
- Kopřiva J. Rychlostní a vytrvalostní složka výkonnosti v lokomočních sportech. Teor. praxe těl.vých. 38, 1990, č. 10, str. 603–
DATA.8,1.5039,1.5,3.3176,2,4.5286,3,7.2509,5,12.3936,10,16.2275
a:
READ x, t: ON ERROR GOTO v
y = 60 * INT(t) + 100 * (t – INT(t))
x = LOG(x): y = LOG(y)
sx = sx + x: kx = kx + x * x
sy = sy + y: ky = ky + y * y
xy = xy + x * y: n = n + 1: GOTO a
v:
j = kx – sx * sx / n
k = ky – sy * sy / n
c = xy – sx * sy / n
b = c / j
a = (sy – b * sx) / n: a = EXP(a)
r = c / SQR(j * k)
PRINT "t1,n,r="; a; " "; b; " "; r
b:
INPUT "l="; l
t = a * l ^ b
m = INT(t / 60)
s = t – 60 * m
PRINT "t="; m; ":"; s
GOTO b
END
Z dat, uvedených v řádku DATA dostaneme výsledek, uvedený v textu. Pro některé další světové rekordmany uvádíme data a vyhodnocení:
|
Plavec Grant Hackett, Australie, světový rekordman na 1500 m kraul s osobními rekordy: |
||||
|---|---|---|---|---|
| 200m | 1:46,11 | t = 51,72 · L1,048 | regresní hodnoty: | 1:46,94 |
| 400m | 3:42,51 | r = 0,99993 | 3:41,11 | |
| 800m | 7:42,51 | 7:37,18 | ||
| 1500m | 14:34,56 | 14:43,48 | ||
| Rychlobruslař Jochem Uytdehage, Holandsko | ||||
| 1,5 km | 1:44,57 | t = 68,10 · L1,05864 | regresní hodnoty | 1:44,61 |
| 5 km | 6:14,66 | r =0,99999954 | 6:14,22 | |
| 10 km | 12:58,92 | 12:59,14 | ||
| Cyklista Chris Boardman, Velká Britanie | ||||
| 4 km | 4:11,114 | t = 64,235 · L0,99968 | regresní hodnoty | 4:16,82 |
| 5km | 5:27,039 | r = 0,99990 | 5:21,01 | |
| 10km | 10:47,102 | 10:41,87 | ||
| 20km | 21:23,932 | 21:23,46 | ||
| 56,3759 km | 1 hod. | 1:00:16,69 | ||
V tomto případě jsou časy kromě 4 km z jediného závodu – hodinovky. Proto klesl exponent pod 1,00.
H09 Zlepšování sportovních výsledků v čase
Různé sportovní discipliny se zlepšují různě rychle. Tato rychlost je dána povahou discipliny. Na příklad skok o tyči se může zdokonalovat mnohem rychleji, nežli běh na 100 m. Rychlost zlepšování lze popsat relativním zlepšením v % za určitou dobu, na příklad rok.
Relativní zlepšení výsledku v1 na v2 je
Čas mezi dvěma daty v dd.mm.rrrr (den.měsíc.rok) přepočítáme na roky a jejich desetinné zlomky pomocí vzorce
Malé chyby z výpočtu s měsíci stejné délky můžeme zanedbat. Procentní zlepšení za 1 rok je
Tyto výpočty lze provést následujícím programem:
a:
INPUT "dd.mmrrrr 1"; a
INPUT "vysledek 1(sek nebo m) "; b
INPUT "dd.mmrrrrr 2"; c
INPUT "vysledek 2(sek nebo m)"; d
d1 = INT(a): m = 100 * (a – d1)
m1 = INT(m): r1 = 10000 * (m – m1)
d2 = INT(c): m = 100 * (c – d2)
m2 = INT(m): r2 = 10000 * (m – m2)
t = r2 – r1 + (m2 – m1) / 12 + (d2 – d1) / 365
z = (d – b) / b
p = z / t * 100
PRINT "zmena % za rok "; p
PRINT: GOTO a
END
| muži | p | ženy | p | |||
|---|---|---|---|---|---|---|
| 100 m | 10,8 | 17.7.1900 | 13,4 | 1.9.1917 | ||
| 9,78 | 14.9.2002 | -,0913% / r | 10,49 | 16.7.1988 | -,306% / r | |
| 200 m | 21,6 | 31.8.1904 | 27,8 | 28.8.1922 | ||
| 19,32 | 2.9.1996 | -,115% / r | 21,34 | 29.9.1988 | -,351% / r | |
| 400 m | 50,4 | 7.6.1867 | 1:01,9 | 15.9.1945 | ||
| 43,18 | 26.8.1999 | -,108% / r | 47,60 | 6.10.1985 | -,576% / r | |
| 800 m | 1:56,0 | 1.9.1904 | 2:30,2 | 20.8.1922 | ||
| 1:41,11 | 24.8.1997 | -,138% / r | 1:53,28 | 26.7.1983 | -,403% / r | |
| 1 km | 2:32,3 | 22.6.1913 | 3:08,2 | 15. 8. 1926 | ||
| 2:11,96 | 5.9.1999 | -,154% / r | 2:28,98 | 25.8.1996 | -,297% / r | |
| 1,5 km | 4:16,8 | 20.5.1845 | 4:37,8 | (1.7).1946 | ||
| 3:26,00 | 14.7.1998 | -,130% / r | 3:50,46 | 11.9.1993 | -,361% / r | |
| 1 míle | 4:56,0 | (1.7).1864 | 4:59,6 | (1.7).1954 | ||
| 3:43,13 | 7.7.1999 | -,188% / r | 4:12,56 | 14.8.1996 | -,372% / r | |
| 2 km | 5:30,4 | 16.6.1918 | 5:43,94 | 17.4.1976 | ||
| 4:44,79 | 7.9.1999 | -,170% / r | 5:25,36 | 9.7.1994 | -,296% / r | |
| 3 km | 8:36,8 | 12.7.1912 | 9:23,4 | (1.7).1971 | ||
| 7:20,67 | 1.9.1996 | -,175% / r | 8:06,11 | 2.9.1993 | -,618% / r | |
| 2 míle | 9:09,6 | 11.6.1904 | ||||
| 7:58,62 | 20.7.1997 | -,139% / r | ||||
| 5 km | 14:36,7 | 10.7.1912 | 15:52,27 | (15).4.1977 | ||
| 12:39,36 | 13.6.1998 | -,155% / r | 14:28,09 | 23.10.1997 | -,436% / r | |
| 10 km | 30:58,8 | 16.11.1911 | 34:01,4 | (1.7).1975 | ||
| 26:22,75 | 1.6.1998 | -,173% / r | 29:31,78 | 8.9.1993 | -,726% / r | |
| 1 hodina | 18555 | 28.7.1884 | ||||
| 21101 | 30.3.1991 | +,128% / r | ||||
| Maratón | 2:58:50 | 10.4.1896 | 3:15:22,8 | 15).5.1967 | ||
| 2:05:38 | 14.4.2002 | -,281% / r | 2:15:25 | 12.4.2003 | -,854% / r | |
| 110m př. | 14,4 | 29.5.1920 | 100m 13,2 | (15).6.1965 | ||
| 12,91 | 20.8.1993 | -,141% / r | 12,21 | 20.8.1988 | -,323% / r | |
| 400 m př. | 55,0 | 22.7.1908 | 56,83 | (1.7).1973 | ||
| 46,78 | 5.8.1992 | -,178% / r | 52,61 | 11.8.1994 | -,351% / r | |
| 3 km př. | 10:47,8 | 22.7.1908 | 9:48,88 | 31.7.1999 | ||
| 7:53,17 | 16.8.2002 | -,287% / r | 9:16,51 | 27.7.2002 | -1,445% / r | |
| Skok vysoký | 197 | (1.7).1895 | 155 | 2.8.1926 | ||
| 245 | 27.7.1993 | +,248% / r | 209 | 30.8.1987 | +,570% / r | |
| Skok daleký | 761 | 5.8.1901 | 516 | 6.8.1922 | ||
| 895 | 30.8.1991 | +,195% / r | 752 | 11.6.1988 | +,694% / r | |
| Skok o tyči | 330 | 10.4.1896 | 375 | (15).7.1988 | ||
| 615 | 21.2.1993 | +,891% / r | 481 | 9.6.2001 | +2,17% / r | |
| Trojskok | 15,39 | 31.7.1909 | 13,79 | (1.7).1985 | ||
| 18,29 | 7.8.1995 | +0,219% / r | 15,50 | 10.8.1995 | +1,226% / r | |
| Koule | 14,81 | 31.8.1904 | 10,84 | 28.5.1927 | ||
| 23,12 | 21.5.1990 | +,654% / r | 22,63 | 7.6.1987 | +1,811% / r | |
| Disk | 34,04 | 12.9.1896 | 34,15 | 20.5.1926 | ||
| 74,08 | 6.6.1986 | +1,310% / r | 76,80 | 9.7.1988 | +2,009% / r | |
| Oštěp | 54,82 | 17.7.1908 | 35,49 | 11.7.1926 | ||
| 98,48 | 25.5.1996 | +,906% / r | 80,00 | 9.9.1988 | +2,016% / r | |
| Kladivo | 49,73 | 16.7.1900 | 48,06 | 27.4.1987 | ||
| 86,74 | 30.8.1986 | +,864% / r | 76,07 | 29.8.1999 | +4.59% / r | |
H10 Dlouhodobé tabulky sportovních výkonů
Dlouhodobé tabulky deseti (nebo více) nejlepších výkonů všech dob obsahují nejlepší výkony bez ohledu na rok výkonu. Na příklad v roce 1968 skočil na OH v México City Bob Beamon světový rekord ve skoku dalekém výkonem 890 cm. Koncem tohoto roku platila tato dlouhodobá tabulka:
| pořadí |
invertované pořadí |
jméno |
výkon (cm) |
rok |
|---|---|---|---|---|
| 1 | 10 | Beamon | 890 | 1968 |
| 2 | 9 | Boston | 835 | 1965 |
| 3 | 8 | Ovanesjan | 836 | 1967 |
| 4 | 7 | Davies | 825 | 1968 |
| 5 | 6 | Brown | 821 | 1949 |
| 6 | 5 | Beer | 819 | 1968 |
| 7 | 4 | Steele | 818 | 1948 |
| 8 | 3 | Ahey | 817 | 1962 |
| 9 | 2 | Hopkins | 816 | 1964 |
| 10 | 1 | Robinson | 816 | 1965 |
Z této tabulky můžeme vypočítat řadu zajímavých ukazatelů:
- aritmetický průměr m = Sx / 10 = 829,2 cm ukazuje stav disciplíny a při srovnání s jinými roky její vývoj. Mohl by také sloužit jako základní údaj při návrhu bodovacích tabulek pro skok daleký.
- směrodatná odchylka sx = 22,55 cm je mírou rozptýlení výkonů, ale nehodí se ke srovnávání, protože má rozměr cm a závisí na zvolených jednotkách.
- variační součinitel v % = 100 · sx / m = 2,72 %. Jím můžeme srovná- vat rozptýlení výkonů v různých disciplinách: u nových a mladých disciplin (skok o tyči žen) bývá větší (přes 2 %), u starých a přirozených disciplin (běh 100 m) bývá malý (i pod 0,5 %).
- poslední výkon v tabulce je současně limitem dalších výkonů v dalších letech vývoje.
- číselný histogram nahrazuje grafický, a říká, kolik výkonů spadá do 10 stejně širokých intervalů mezi nejlepším a nejhorším výkonem. V uvedené tabulce je rozpětí výkonů 890-816 = 74 cm. 10 intervalů po 7,4 cm je pak obsazeno takto: 10000 000216.
Rovnoměrně rozdělené výkony by měly histogram 11111 11111.první jednička světový rekord (890 cm) osmá dvojka výkony 835,835 cm devátá jednička výkon 825 cm desátá šestka výkony 821-816 cm.
Největší odstup od ostatních: histogram 10000 00009
Nejmenší odstup od ostatních 90000 00001.
Kromě tohoto histogramu musíme vzít v úvahu i variační součinitel.
Beamon i Griffith-Joynerová (100m běh 10,43 s) mají stejný histogram, ale liší se podstatně variačním součinitelem: Beamonova tabulka má v = 2,72 %, Griffith-Joynerové v = 1,03 %. Proto je Beamonův výkon výjimečnější a byl také nazván "skokem do 21. století".
-
index výjimečnosti přepočítává histogram na jediné číslo využitím pořadí v tabulce. Číslo pořadí násobíme stejnolehlým číslem histogramu a součiny sečteme:
Beamon má 1x1 + 2x8 + 1x9 + 6x10 = 86.
Histogram s rovnoměrným rozdělením 11111 11111 by dal 51, maximální 10000 00009 dá index 91, minimální 90000 00001 dává index 10.
- ukazatel historického významu sportovce dostaneme pomocí inverzního pořadí (viz tab.). Sečteme inversní pořadí sportovce za celou dobu, po kterou se vyskytoval v tabulkách. Na příklad Beamon se výkonem 890 cm zařadil na první místo, kde zůstal do roku 1990, tedy 23 let. Součin s 10 body za první místo dává 230 bodů
V letech 1991–2000 (10 let) byl druhý po 9 bodech, celkem 90 bodů
Celkový součet k 1. 1. 2001 je 320 bodů a ještě v budoucnosti poroste, dokud Beamon nevypadne z tabulky. Tento ukazatel pomáhá najít nejvýznamnějšího sportovce minulosti, neuvažujeme-li jeho úspěchy na olympijských hrách, mistrovství světa nebo Evropy či počet světových rekordů a jiné skutečnosti.
Literatura
- Kopřiva J.: Bodování a vývojová tabulka sportovních výsledků Teor. praxe těl. vých. 26, 1978, č.10, str.637–639
Popsané ukazatele snadno vypočítáme programem:
DATA x1,x2,… x10
mi=1E6:ma=0:DIM m(10),c(10)
FOR i=1 TO 10
READ m(i):s=s+m(i)
k=k+m(i)*m(i)
IF m(i)<mi THEN mi=m(i)
IF m(i)>ma THEN ma=m(i)
NEXT i
m=s/10: w=(ma-mi)/9.999
FOR i=1 TO 10
r=INT((m(i)-mi)/w)+1
c(r)=c(r)+1: NEXT i
sx=SQR((k-sx*sx/10)/9): v=100*sx/m
PRINT "prům,sx,v%=";m,sx,v
IF m(1)<m(10) THEN GOTO a
FOR i=10 TO 1 STEP –1
PRINT c(i);:NEXT i:END
a:
FOR i=1 TO 10
PRINT c(i);:NEXT i
END
H11 Zdánlivá velikost branek a terčů
Sportovec, střílející na branku nebo terč v míčových hrách nebo střeleckých disciplinách má větší naději na zásah, jestliže branka nebo terč jsou
- velké
- blízko
- kolmo na směr míče nebo střely či šípu.
Při kolmém pohledu se jeví zdánlivá šířka branky úměrná úhlu a = šířka / vzdálenost. Výška branky se analogicky jeví jako b = výška / vzdálenost. Plocha branky je jeví jako úměrná součinu
Tak je ale definován prostorový úhel, který měříme ve steradiánech (srad). Pro míčové hry můžeme počítat prostorové úhly branek z místa volných nebo trestných kopů či hodů, pro střelecké sporty prostorové úhly terčů ze známých vzdáleností. Zde jsou výsledky:
| SPORT | branka | plocha | vzdálenost | prost. úhel (srad) |
|---|---|---|---|---|
| kopaná | 7,32 × 2,44 m | 17,84 m2 | 11 m | 0,147416 |
| halový kop. | 3 × 2 m | 6 m2 | 7 m | 0,12245 |
| házená | 3 × 2 m | 6 m2 | 7 m | 0,12245 |
| hokej | 1,83 × 1,22 m | 2,2297 m2 | ? | |
| pozemní hokej | 3,66 × 2,14 m | 7,8324 m2 | 6,4 m | 0,19122 |
| kolová | 2 × 2 m | 4 m2 | 4 m | 0,25 |
| vodní pólo | 3 × 0,9 m | 2,7 m2 | 4 m | 0,16875 |
|
Střelecké sporty: |
terč D(m) |
desítka d(m) |
vzdálenost L(m) |
prost. úhel srad (x104) |
desítky srad (x107) |
|---|---|---|---|---|---|
| lukostřelba | 1,22 | 0,061 | 90 | 1,443 | 3,608 |
| lukostřelba | 1,22 | 0,061 | 70 | 2,386 | 5,964 |
| ženy | 1,22 | 0,061 | 60 | 3,247 | 8,118 |
| krátké vzdál. | 0,80 | 0,05 | 50 | 2,011 | 7,754 |
| 30 | 5,585 | 21,82 | |||
| libovolná pistole | 0,5 | 0,05 | 50 | 0,7854 | 7,854 |
| velkorážní pistole | 0,5 | 0,05 | 25 | 3,142 | 31,42 |
| standardní pistole | 0,5 | 0,05 | 25 | 3,142 | 31,42 |
| vzduchová pistole | 0,156 | 0,012 | 10 | 1,911 | 11,31 |
| malorážka | 0,1624 | 0,0124 | 50 | 0,08268 | 0,4831 |
| standardní puška | 1 | 0,1 | 300 | 0,08727 | 0,8727 |
| vzduchovka | 0,046 | 0,001 | 10 | 0,1662 | 0,0077 |
| skeet | 0,11 | 19,2 | 0,2578 | ||
| baterie | 0,11 | 15 | 0,4224 |
Při šikmých úhlech je nutné násobit prostorový úhel kosinem úhlu, měřeného od kolmice. Volný hod v košíkové je analyzován v kapitole míčových her.
H12 Vyhodnocení intervalového tréninku v lokomočních sportech
Hledá-li trenér nebo sportovec souvislost mezi tréninkem a závodním výkonem, je na jedné straně poměrně složitý proces tréninkový, který lze popsat řadou parametrů, a na druhé straně poměrně jednoduchý výsledek závodu. Aby se složitost obou srovnávaných informací přiblížila, je nutné popsat tréninkovou jednotku zmenšeným počtem ukazatelů s vysokým informačním obsahem. Ty musí tréninkový proces vyhodnotit kvantitativně i kvalitativně.
Kvantitu intervalového tréninku lze popsat délkou úseků, jejich počtem a celkovou délkou nebo dobou trvání tréninku.
Kvalitu intervalového tréninku popisuje buď vynaložené úsilí nebo rychlost lokomoce. Protože zatím nebylo nalezeno žádné přijatelné stanovení nebo dokonce měření úsilí, zůstává měřítkem kvality nebo intensity tréninku poměr rychlosti tréninkové k závodní. Intensitu závodu položíme rovnu jedničce (100 %). Abychom nemuseli rychlost počítat, použijeme přímo časů nebo průměrů časů v obráceném poměru:
Třetí mocninu lze zdůvodnit fyziologicky, protože se stejnou mocninou rychlosti roste výdej energie. Plyne to z fyziologických měření, jejichž výsledky uvádějí knihy o fyziologii sportu. Např. [76] uvádí pro různé sporty tabulky dvojic rychlost-výdej, z nichž aproximací metodou nejmenších čtverců dostaneme řadu funkcí, které s vysokou korelací nahrazují experimentální data:
| běh | N(kW) = 0,58. exp(0,039.v2) | r=0,996 |
| chůze | N(kW) = 0,105. exp(0,853.v) | r=0,9983 |
| plavání | ||
| kraul | N(kW) = 0,439 · v3,02 | r=0,9949 |
| znak | N(kW) = 0,385 · v4,02 | r=0,9987 |
| delfín | N(kW) = 0,89 · v2,27 | r=0,9995 |
| prsa | N(kW) = 1,184 · v2,097 | r=0,999 |
| cyklistika | N(kW) = 0,0103 · v1,3557 | r=0,996 |
| rychlobruslení | N(kW) = 0,00423 · v1,6777 | r=0,994 |
Práce, vykonaná v n-úsecích, trvajících t sekund je pak
Ze známých osobních rekordů můžeme počítat intensity podle (1) a pomocí intensity roztřídíme práce na úsecích do intensitních pásem 0,5 až 1 (po 0,1). Praxe ukázala, že trénink intensity nižší nežli 0,5 nemá fyziologický účinek. Z tohoto rozdělení práce na různé intensity můžeme počítat váženou průměrnou intensitu
a doplnit celkovou délkou tréninku
Literatura
- Seliger V., Vinařický R., Trefný Z.: Fysiologie tělesných cvičení 1980, Praha, Avicenum, str. 23, tab.1
- Vinařický R. Výdej energie při sportovní činnosti. Tělovýchovný sborník 10, 1967, 77
- Vinařický R., Kubalová S., Frank V., Vodička P. Výdej energie při lehkoatletických bězích, vztah rychlosti běhu a výdeje energie, využití individuálních rozdílů v tréninkové praxi. Teor. praxe těl. vých.19, 1971, 722
- Kopřiva J. Vyhodnocení tréninkového deníku v lokomočních sportech grafem nebo počítačem. Teor. praxe těl. vých, 37, 1989, 261
DIM V(20), W(20), A(20), I(20), S(20): J = 1: C = 0
LPRINT " rych "; " vykon "; " prace "; " intensita"
A:
INPUT "L,N,T,Tr="; L, N, T, TR
V(J) = L / T: W(J) =.58 * EXP(.039 * V(J) * V(J))
A(J) = W(J) * T * N: I(J) = (TR / T) ^ 3: C = C + L * N
LPRINT L; USING "#####.###"; V(J); W(J); A(J); I(J)
INPUT "dalsi trat? a/n"; x$: IF x$ <> "a" THEN GOTO B
J = J + 1: GOTO A
B:
FOR K = 1 TO J
M = (I(K) –.5) * 10: S(M) = S(M) + A(K): NEXT K
LPRINT "intensita-prace"
FOR M = 1 TO 4: LPRINT M / 10 +.5; S(M)
NEXT M
FOR K = 1 TO J
SI = SI + A(K) * I(K): SA = SA + A(K): NEXT K
IP = SI / SA: LPRINT "prum.intensita="; IP
LPRINT "celk.delka="; C
LPRINT "celk.prace="; SA; "kJ": END
Fakulta sportovních studií, Masarykova univerzita |
Návrat na úvodní stránku webu, přístupnost |
| Servisní středisko pro e-learning na MU
| Fakulta informatiky Masarykovy univerzity, 2011
Technické řešení této výukové pomůcky je spolufinancováno Evropským sociálním fondem a státním rozpočtem České republiky.