3 Štatistická indukcia – teoretická časť

Dôležitou súčasťou analýzy dát je testovanie štatistických hypotéz. Pri skúmaní závislosti dvoch náhodných veličín je obsahom testovanej nulovej hypotézy tvrdenie, že náhodné veličiny sú nezávislé oproti alternatívnej hypotéze, že náhodné veličiny sú závislé. V tejto kapitole sa zameriame na testy nezávislosti pomocou už známych korelačných koeficientov a taktiež na testy modifikovaných hypotéz o korelačných koeficientoch.

Ako každé testovanie, aj testovanie nezávislosti musí spĺňať určité predpoklady. Predpoklady testovania nezávislosti pri použití Pearsonovho (výberového) korelačného koeficienta sú, že náhodný výber pochádza z dvojrozmerného normálneho rozdelenia pre veličiny intervalového či pomerového typu, medzi ktorými možno predpokladať linearitu. Pri porušení týchto predpokladov, alebo v prípade veličín čisto ordinálneho typu, používame Spearmanov korelačný koeficient. Pri tvorbe kapitoly sme čerpali z [11], [9], [4], [3].

3.1 Predpoklad normality

Uvažujme normálne rozdelený náhodný vektor $(X,Y)^{'}$ so simultánnou hustotou

Marginálne hustoty sú

Z predchádzajúcich kapitol vieme, že veličiny $X$ a $Y$ sú nekorelované, ak sa ich korelačný koeficient $R$, v literatúre často označovaný ako $\rho$, rovná nule a nezávislé, pokiaľ platí $F(x,y)=F_1(x)F_2(y)$ pre $ \forall (x,y) \in \mathbb{R}^2$, v obecnom prípade. Dosadením nulovej hodnoty korelačného koeficienta do vzorca simultánnej hustoty normálneho rozdelenia potom dostávame

Je zrejmé, že v tomto prípade platí $ f(x,y)=f_1(x)f_2(y)$ pre $\forall (x,y) \in \mathbb{R}^2$. Normalita náhodných veličín teda zaisťuje, že nekorelovanosť odpovedá nezávislosti, a preto sa pri testovaní nezávislosti môžeme opierať o Pearsonov korelačný koeficient. To, ako sa tento koeficient (resp. jeho odhad) aplikuje pri testovaní, si ukážeme v nasledujúcej časti.

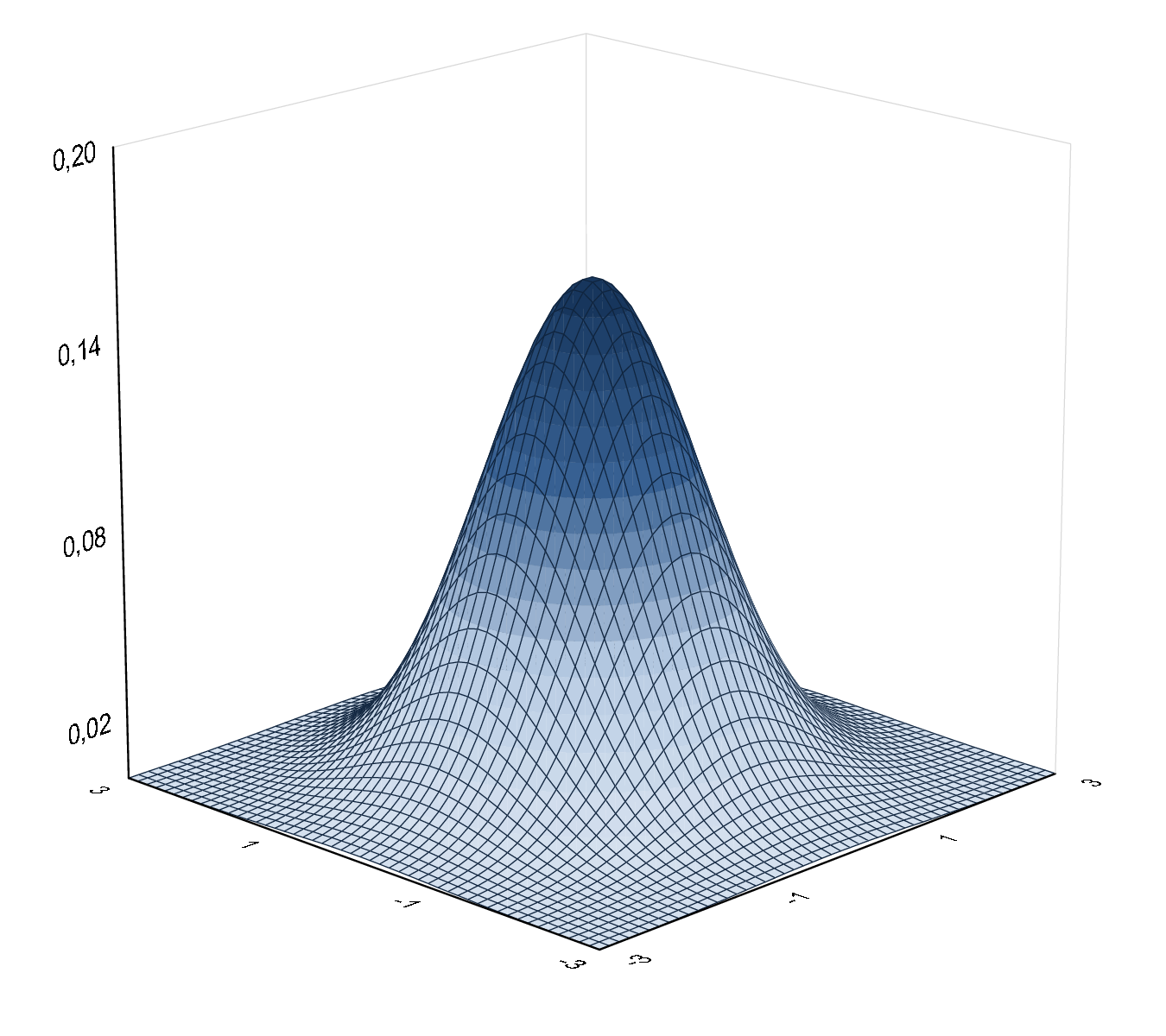
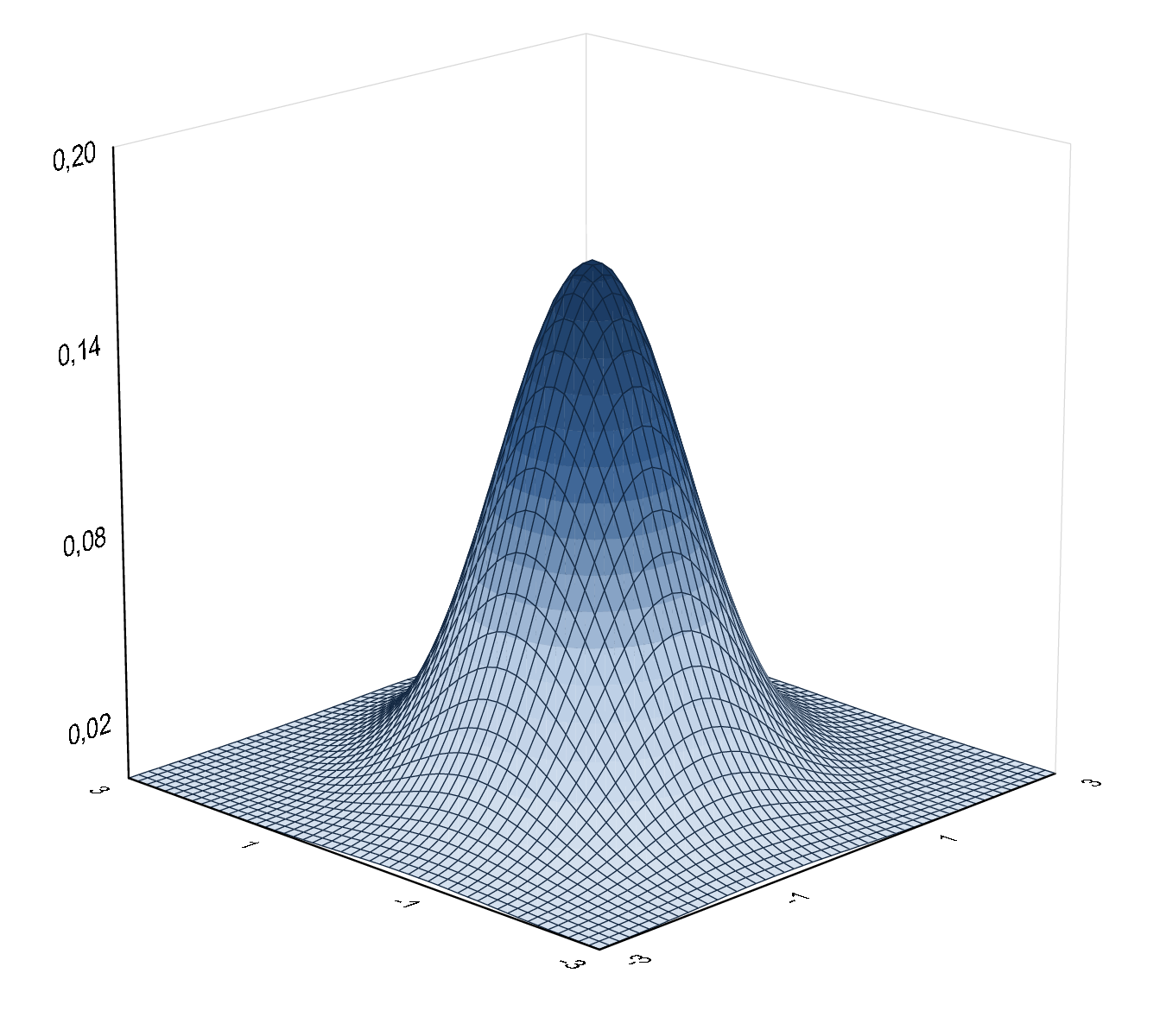
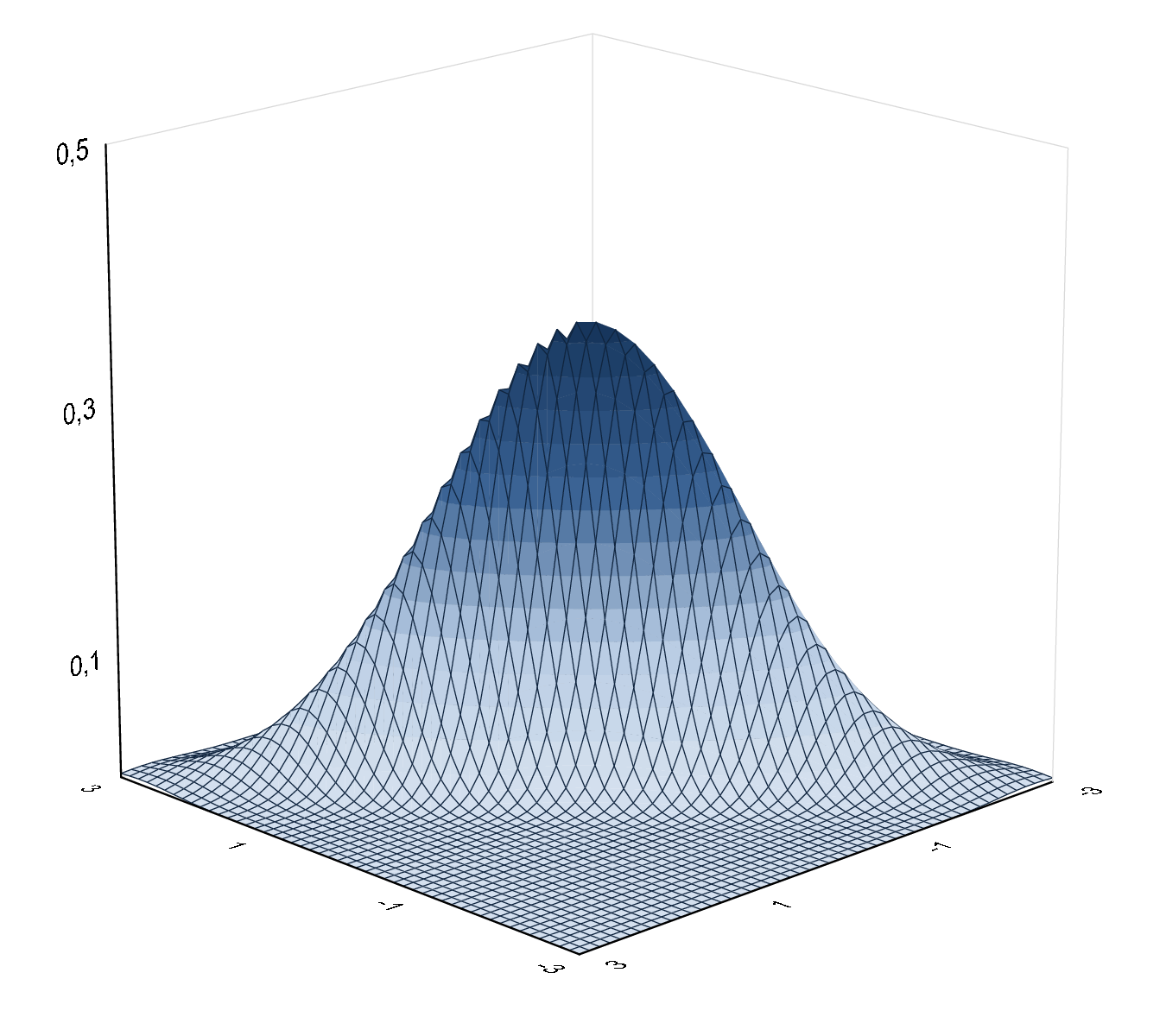
Dvojrozmernú normalitu vieme orientačne posúdiť z bodového grafu. V prípade dostatočne veľkého počtu pozorovaní by mali body grafu vytvoriť obrazec elipsy, pretože vrstevnice hustoty dvojrozmerného normálneho rozdelenia sú elipsy.

Na ukážku toho si zobrazíme tri rôzne grafy hustoty dvojrozmerného normálneho rozdelenia s nulovými strednými hodnotami a jednotkovými rozptylmi, ktoré sa líšia v hodnote parametra korelačného koeficienta, a k nim odpovedajúce vrstevnice. V prípade nulového korelačného koeficienta ide o štandardizované dvojrozmerné normálne rozdelenie, kedy vrstevnice hustoty tohto rozdelenia tvoria kružnice, viď obrázok 3.1. S rastúcou, resp. klesajúcou absolútnou hodnotou koeficienta majú vrstevnice elipsovitejší tvar ako môžeme vidieť na obrázkoch 3.2, 3.3.

3.2 Test významnosti korelačného koeficienta

Uvažujme náhodný výber $(\mathbb{X},\mathbb{Y})$ z dvojrozmerného normálneho rozdelenia rozsahu $n$, s korelačným koeficientom $R$ a výberovým korelačným koeficientom $R_{12}$.

Výberový korelačný koeficient $R_{12}$ interpretujeme ako bodový odhad korelačného koeficienta $R$. Kedže sa jedná o výberovú charakteristiku, jeho nenulová hodnota nemusí znamenať, že aj skutočný korelačný koeficient je nenulový. V praxi sa preto vyžaduje otestovať, či je zistená hodnota výberového korelačného koeficienta štatisticky významná pre tvrdenie, že medzi skúmanými veličinami $X$, $Y$ skutočne existuje závislosť.

Odpoveď na túto otázku môžeme získať z testu významnosti korelačného koeficienta, ktorý uskutočníme pomocou kritického oboru pre štatistiku $T$, viď (3.1) alebo intervalu, ktorý je na tejto štatistike založený.

Testujeme nulovú hypotézu

tj. hypotézu o nezávislosti náhodných veličín $X$ a $Y$, oproti niektorej alternatívnej hypotéze:

• obojstranná alternatíva:\[H_1 \colon R\ne 0,\textit{ tj. veličiny $X$ a $Y$ sú stochasticky závislé,}\]
• pravostranná alternatíva:\[H_1 \colon R\gt 0, \textit{ tj. veličiny $X$ a $Y$ sú kladne korelované,}\]
• ľavostranná alternatíva:\[H_1 \colon R \lt 0, \textit{ tj. veličiny $X$ a $Y$ sú záporne korelované.}\]

Ako testovacie kritérium používame štatistiku

Štatistika $T$ sa pri platnosti nulovej hypotézy riadi Studentovým rozdelením s $(n-2)$ stupňami voľnosti.

Na zvolenej hladine významnosti $\alpha$ zamietame nulovú hypotézu vtedy, keď sa štatistika $T$ realizuje v kritickom obore $W$. Kritický obor má tvar

V prípade, že je rozsah výberu $n>30$, je možné Studentovo rozdelenie aproximovať štandardizovaným normálnym rozdelením $N(0,1)$ a kritický obor upraviť nahradením kvantilov Studentovho rozdelenia kvantilmi štandardizovaného normálneho rozdelenia.

Test hypotézy o nezávislosti môžeme uskutočniť pomocou nasledujúcich intervalov, ktoré sa odvádzajú na základe skutočnosti, že testovacia štatistika $T$ sa za platnosti nulovej hypotézy riadi Studentovaým rozdelením s~$(n-2)$ stupňami voľnosti. \[P\left(t_{\alpha/2}(n-2)\lt T \lt t_{1-\alpha/2}(n-2)\right)= 1-\alpha \text{,}\] odkiaľ úpravou nerovností a nahradením odhadu $R_{12}$ koeficientom $R$ dostaneme

kde $D$ je dolná a $H$ je horná hranica intervalu, ktorý má tak tvar:

Ak hodnota výberového korelačného koeficienta nespadá do daného intervalu $(D,H)$, resp. $( -\infty,H)$ alebo alebo $(D,\infty)$, nulovú hypotézu o nezávislosti veličín $X$ a $Y$ zamietame na hladine významnosti $\alpha$ v prospech alternatívnej hypotézy.

Využitím štatistického systému pri testovaní hypotézy o korelačnom koeficiente zamietame nulovú hypotézu, pokiaľ je $p$-hodnota daného testu menšia alebo rovná ako zvolená hladina významnosti $\alpha$. Toto kritérium platí pre všetky nasledujúce testy.

3.3 Interval spoľahlivosti pre korelačný koeficient

Pri náhodnom výbere z dvojrozmerného normálneho rozdelenia a pre hodnoty koeficientu $R$ blízke nuleAk pre korelačný koeficient platí $\vert R\vert \lt 0,5$ a pre rozsah výberu platí $n>100$, potom môžeme rozdelenie výberového korelačného koeficienta aproximovať normálnym rozdelením. V tomto prípade sa pre koeficient $R$ používa $100(1-\alpha)\%$ interval spoľahlivosti, uvedený napr. v [9], str. 173 alebo v [4], str. 134. je možné považovať výberové rozdelenie koeficientu $R_{12}$ za približne normálne. Pre obecný prípad $-1\lt R\lt 1$ sa však výberové rozdelenie s rastúcim $R$ stále viac zošikmuje, a preto je konštrukcia asymptotického intervalu spoľahlivosti pre $R$ založená na Fisherovej Z-transformácii výberového korelačného koeficienta.

Transformovaná náhodná veličina

Štandardizáciou veličiny $Z$ dostaneme veličinu

ktorá ma asymptoticky štandardizované normálne rozdelenie $N(0,1)$.

Interval spoľahlivosti pre strednú hodnotu veličiny $Z$, $E(Z)^*$Strednú hodnotu berieme so zanedbaným druhým sčítancom.$=\frac{1}{2}\mathrm{ln}\frac{1+R}{1-R}$, vyjadríme z

úpravou nerovností do tvaru

Interval spoľahlivosti pre korelačný koeficient $R$ potom dostaneme spätnou trasformáciou.

Keďže $Z=\mathrm{arctgh}\,R_{12}$, potom $R_{12}=\mathrm{tgh}\,Z $ a hranice intervalu spoľahlivosti môžeme písať v tvare

Tento interval spoľahlivosti môžeme použiť pri testovaní nulovej hypotézy o danej hodnote koeficienta korelácie, viď sekcia 3.4. Nulovú hypotézu zamietame na asymptotickej hladine významnosti $\alpha$ v prospech alternatívnej hypotézy v prípade, že sa daná hodnota v intervale spoľahlivosti nenachádza.

3.4 Test hypotézy o danej hodnote korelačného koeficienta

Tento test umožňuje overiť zhodu korelačného koeficienta s danou konštantou $c$, pre ktorú platí $c \in (-1,1)$. Testujeme nulovú hypotézu

oproti niektorej z alternatívnych hypotéz

Testovacia štatistika je

Štatistika $U$ má za platnosti nulovej hypotézy pre $n\geq 10$ asymptoticky rozdelenie $N(0,1)$. Ak vypočítaná hodnota testovacej štatistiky padne do kritického oboru

nulovú hypotézu zamietame na asymptotickej hladine významnosti $\alpha$.

3.5 Test zhody dvoch korelačných koeficientov

Zoberme do úvahy situáciu, že máme k dispozícii dva nezávislé náhodné výbery rozsahov $n$ a $n^*$ z dvojrozmerných normálnych rozdelení s koeficientami korelácie $R$ a $R^*$. Zaujíma nás, či sa ich korelačné koeficienty štatisticky významne líšia, tj. či oba výbery pochádzajú z rovnakého základného súboru. Testujeme preto nulovú hypotézu

Ak označíme výberové korelačné koeficienty výberov $R_{12}^{\phantom{*}}$ a $R_{12}^*$, potom ich Fisherove Z-transformácie sú

Testovacie kritérium je štatistika

ktorej rozdelenie, pri platnosti $H_0$ a podmienke $n\geq 10$, je asymptoticky $N(0,1)$. Kritický obor pre test hypotézy $H_0$ oproti $H_1$ je

Ak realizácia štatistiky $U$ leží v kritickom obore $W$, potom $H_0$ zamietame na asymptotickej hladine významnosti $\alpha$.

3.6 Test zhody k korelačných koeficientov

Tento test je zovšeobecnením predchádzajúceho testu, ktorý umožňuje testovať zhodu $k>2$ korelačných koeficientov.

Budeme predpokladať, že máme k dispozícii $k$ navzájom nezávislých náhodných výberov z dvojrozmerných normálnych rozdelení s korelačnými koeficientami $R_1,R_2,\ldots ,R_k$ a rozsahmi $n_1,n_2,\ldots,n_k$, pre ktoré platí $n=n_1+n_2+\cdots+n_k$. Odpovedajúce výberové korelačné koeficienty označíme ako $R_{12}^1,R_{12}^2,\ldots,R_{12}^k$.

Testujeme nulovú hypotézu

Testovacie kritérium je štatistika

kde $b=\frac{1}{n-3k}\cdot\sum_{i=1}^k(n_i-3)Z_i$ a $Z_i$ je Fisherova Z-transformácia výberového korelačného koeficienta $R_{12}^i$ daná vzťahom (3.2), pre $i=1,2,\ldots,k$.

Za platnosti nulovej hypotézy má štatistika $\chi^2$ asymptoticky $\chi^2$ rozdelenie s $(k-1)$ stupňami voľnosti a kritický obor

V prípade, že nulovú hypotézu o zhode $k$ korelačných koeficientov zamietneme, využijeme Tukeyov test, podľa ktorého zistíme, ktoré korelačné koeficienty sa od seba štatisticky významne líšia. Pre každú dvojicu $i\lt j$ ($i,j=1,\ldots,k$) určíme nerovnosť

Štatisticky významne sa od seba líšia tie koeficienty, pre ktoré daná nerovnosť platí.

3.7 Test významnosti Spearmanovho korelačného koeficienta

Konečne sa dostávame k problému, kedy nemôžeme apriorne prijať predpoklad normality. V takomto prípade sa pri testovaní nezávislosti náhodných veličín $X$ a $Y$ používa metóda určená pre náhodné veličiny ordinálneho typu. Táto neparametrická metóda je založená na Spearmanovom korelačnom koeficiente definovanom v kapitole 2, ktorý spočíva v nahradení konkrétnych hodnôt náhodných veličín ich poradovými číslami.

Obdobne testujeme nulovú hypotézu o nulovej hodnote teoretického Spearmanovho koeficientu korelácie

tj. hypotézu, že veličiny $X$ a $Y$ sú poradovo nezávislé oproti niektorej z alternatívnych hypotéz

Pri výbere malého rozsahu $(n\lt 20)$ slúži ako testovacie kritérium Spearmanov koeficient korelácie $r_s$ vypočítaný podľa vzťahu (2.4), pre ktorý sa kritický obor $W$ zostavuje použitím špeciálnych tabelovaných kritických hodnôtTabelované kritické hodnoty nájdeme v štatistických tabuľkách. štatistiky $r_s$ nasledovne:

Hypotézu o poradovej nezávislosti zamietame na hladine významnosti $\alpha$, ak $r_s \in W$.

V závislosti od rozsahu daného výberu existujú asymptotické varianty tohto testu. Pre $n> 20$ používame testovaciu štatistiku (3.1) nahradením výberového korelačného koeficienta Spearmanovým koeficientom korelácie, tj.

ktorá má za platnosti nulovej hypotézy asymptoticky Studentovo rozdelenie s $(n-2)$ stupňami voľnosti.

Na hladine významnosti $\alpha$ zamietame nulovú hypotézu v prípade, že sa štatistika $T$ realizuje v kritickom obore $W$ totožnom kritickému oboru štatistiky (3.1):

Pre $n>30$ používame testovaciu štatistiku

ktorá má za planosti nulovej hypotézy asymptoticky štandardizované normálne rozdelenie $N(0,1)$. Kritický obor má obdobne tvar

Štatistický systém STATISTICA využíva pri testovaní štatistiku (3.9), bez ohľadu na rozsah výberu.