4 Štatistická indukcia – praktická časť
Doposiaľ získané znalosti z predchádzajúcich kapitol tvoria nutný teoretický základ na nasledujúce použitie v praxi. Obsahom tejto kapitoly bude riešenie praktických príkladov, na ktorých si predovšetkým ukážeme aplikáciu testov uvedených v kapitole kapitola3. Riešenie jednotlivých príkladov bude zahŕňať ručný výpočet a výpočet za pomoci systému STATISTICA. Literárne zdroje použité pri tvorbe príkladov uvádzame vždy samostatne za každým zadaním príkladu.
Pri testovaní hypotéz budeme používať hladinu významnosti $\alpha=0,05$, pokiaľ nebude uvedené inak.
Príklad 1 Test významnosti korelačného koeficienta, 3.2.
Sú dané údaje o 27 vybraných pozemkoch, na ktorých poľnohospodárske závody pestujú v určitej oblasti ozimný jačmeň. Nadmorskú výšku pozemku (v metroch) označíme X, hektárový výnos jačmeňa (v t/ha) Y. Hodnota výberového korelačného koeficienta medzi danými veličinami je $-$0,93. Testujte na hladine významnosti $1\,\%$, či skutočne medzi nimi nepriama závislosť existuje. [12], str. 758 (Dáta dostupné na https://goo.gl/z2sk2q; KORELACE – Environment – E702.)
Pred testovaním závislosti sa uistíme, či daný náhodný výber pochádza z dvojrozmerného normálneho rozdelenia. Postupujeme tak, že najskôr otestujeme normalitu náhodných veličín $X$, $Y$ a následne zobrazíme dvojrozmerný bodový diagram s elipsou $95\%$ konštantnej hustoty pravdepodobnosti, na základe ktorého posúdime dvojrozmernú normalitu dát. Toto overenie uskutočníme využitím systému STATISTICA.
Vytvoríme dátový súbor s 2 premennými a 27 prípadmi. Pomenujeme ich X, Y a do tabuľky zapíšeme odpovedajúce hodnoty. (Tabuľku neuvádzame z dôvodu rozsiahleho počtu pozorovaní.)
Grafické overenie jednorozmernej normality: Grafy – 2D grafy – Normální pravděpodobnostní grafy – odškrtneme Neurčovat prům. pozici svázaných pozorování – Proměnné; X, Y; OK – OK.


Testy hypotézy o normálnom rozdelení náhodných veličín: Statistiky – Základní statistiky/tabulky – Tabulky četností; OK – záložka Normalita; zaškrtneme Lilieforsův test a Shapiro-Wilkův W test – Proměnné; X, Y; OK – Testy normality.

Normálne pravdepodobnostné grafy svedčia v prospech normálneho rozdelenia náhodných veličín, pretože body ležia takmer na alebo v blízkosti danej priamky, o čom svedčia aj výsledky testov hypotézy o normalite; $p$-hodnoty Lilieforsovej varianty Kolmogorovho-Smirnovho testu pre obe veličiny väčšie ako $0,2$ a $p$-hodnoty Shapiro-Wilksovho testu $0,2929$ a $0,3221$. Tieto hodnoty sú väčšie ako daná hladina významnosti $\alpha=0,01$, a preto nulovú hypotézu o normalite náhodných veličín $X$, $Y$ nezamietame.
Dvojrozmerný bodový diagram: Grafy – Bodové grafy – odškrtneme Typ proložení – Proměnné; X, Y; OK – záložka Detaily; Elipsa: normální, Koeficient 0,99 – OK. (Na zobrazenie celej elipsy je potrebné zväčšiť merítko: klikneme pravým tlačitkom na graf – možnosti grafu – osa; merítko a upravíme minimum a maximum podľa potreby)

Vykreslením dvojrozmerného bodového diagramu vidíme, že všetky body ležia vo vnútri elipsy, čo považujeme za splnený predpoklad dvojrozmernej normality.
Na hladine významnosti $1\,\%$ testujeme nulovú hypotézu
\[ \begin{aligned} H_0 \colon R=0 \end{aligned} \text{ oproti } \begin{aligned} H_1 \colon R \lt 0. \end{aligned} \]So známou hodnotou výberového korelačného koeficienta $r=-0,93$ z výberu rozsahu $n=27$ spočítame testovaciu štatistiku $T$:
\begin{align*} t=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}}=\frac{-0,93\cdot 5}{\sqrt{1-(-0,93)^2}}=-12,65 \text{.} \end{align*}V štatistických tabuľkách nájdeme kvantil Studentovho rozdelenia pre spoľahlivosť $1- \alpha$ a stupne voľnosti $n-2$, tj. $t_{0,99}(25)=2,485$ a zostavíme ľavostranný kritický obor $W=( -\infty; -2,485\rangle$. Realizácia testovacej štatistiky $-12,65$ leží v kritickom obore $W$, a preto na hladine významnosti $1\,\%$ zamietame nulovú hypotézu v prospech alternatívnej hypotézy, že medzi veličinami nepriama závislosť skutočne existuje. Znamená to, že s klesajúcou nadmorskou výškou rastie hektárový výnos jačmeňa.
Do úvahy zoberieme to, že máme k dispozícii hodnotu výberového korelačného koeficienta a môžeme tak jednoducho spočítať $p$-hodnotu testu: Statistiky – Pravdpodobnostní kalkulátor – Korelace; vyplníme N: 27, r: $-$0,93; odškrtneme Oboustranné a zaškrtneme Výpočet p z r – Výpočet.
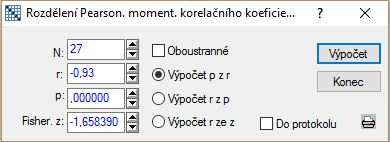
V tabuľke v políčku p sa zobrazila hodnota $0,00000$, čo značí, že je $p$-hodnota testu veľmi malá a teda menšia ako hladina významnosti $0,01$, podľa čoho zamietame na hladine významnosti $1\,\%$ nulovú hypotézu v prospech alternatívnej hypotézy.
Výpočet $p$-hodnoty jednostranného testu z $p$-hodnoty obojstranného testu ozn. $p$ prebieha v závislosti od znamienka výberového korelačného koeficienta. Ak je $r\lt 0$, potom sa $p$-hodnota ľavostranného testu rovná $p/2$, resp. $1-p/2$ pre pravostranný test. Ak je $r>0$, potom sú $p$-hodnoty jednostranných testov presne opačné, tj. $1-p/2$ pre ľavovostranný test a $p/2$ pre pravostranný test. V našom prípade sa teda jedná o $p$-hodnotu ľavostranného testu.
Ďalšou možnosťou riešenia je výpočet z tabuľky dát, kedy nám STATISTICA poskytne, okrem iného, aj hodnotu testovacej štatistiky. Tento spôsob si ukážeme v nasledujúcom príklade.
Príklad 2 Test významnosti korelačného koeficienta, 3.2.
Z uvedených údajov vyjadrite závislosť požadovaného množstva výrobku (v kusoch), ktoré je spotrebiteľ ochotný nakúpiť pri daných cenách (v korunách) a pomocou vhodného testu overte, či sa jedná o štatisticky významnú závislosť. [10], str. 293
| Požadované množstvo | 45 | 55 | 38 | 40 | 40 | 55 | 60 | 60 | 75 | 65 | 55 | 55 | 61 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cena | 40 | 63 | 80 | 89 | 81 | 61 | 50 | 75 | 13 | 36 | 70 | 90 | 80 |
Postup overenia dvojrozmernej normality je analogický ako v predchádzajúcom príklade, naďalej sa ale obmedzíme na testy normality a dvojrozmerný bodový diagram vynechaním normálne pravdepodobnostných grafov.


Pretože sú $p$-hodnoty oboch testov jednorozmernej normality väčšie ako hladina významnosti $0,05$ a v dvojrozmernom bodovom diagrame vypĺňajú body vnútro elipsy, hodnotíme predpoklad dvojrozmernej normality za oprávnený.
Označme požadované množstvo ako veličinu $X$ a cenu ako $Y$. K dispozícii máme výber rozsahu $n=13$. Závislosť medzi veličinami vyjadríme pomocou výberového korelačného koefcienta $R_{12}$. Na jeho výpočet spočítame najprv realizácie výberových priemerov $M_1$ a $M_2$, výberových smerodajných odchýliek $S_1$ a $S_2$ a výberovej kovariancie $S_{12}$:
\begin{align*} m_1&=\frac{1}{n}\sum_{i=1}^n x_i=\frac{1}{13}(45+55+\cdots+61)=\frac{704}{13}=54,154\text{,}\\ m_2&=\frac{1}{n}\sum_{i=1}^n y_i=\frac{1}{13}(40+63+\cdots+80)=\frac{828}{13}=63,692\text{,}\\ s_1&=\small\sqrt{\frac{1}{n-1}\left(\sum_{i=1}^{n} x_i^2 - nm_1^2\right)}=\sqrt{\frac{1}{12}\left(45^2+55^2+\cdots+61^2 - 13\frac{704^2}{13^2}\right)}=10,862\text{,}\\ s_2&=\small\sqrt{\frac{1}{n-1}\left(\sum_{i=1}^{n} y_i^2 - nm_2^2\right)}=\sqrt{\frac{1}{12}\left(40^2+63^2+\cdots+80^2 - 13\frac{828^2}{13^2}\right)}=23,139\text{,}\\ s_{12}&=\small\frac{1}{n-1}\left( \sum_{i=1}^n x_iy_i-nm_1m_2\right)=\frac{1}{12}\left(45\cdot40+55\cdot63+\cdots+61\cdot80-13\frac{704}{13}\frac{828}{13}\right)\text{,}\\ s_{12}&=-157,032\text{.}\\ &\text{Dosadením konkrétnych hodnôt a jednoduchým výpočtom dostávame}\\ r&=\frac{s_{12}}{s_1s_2}=\frac{-1507,032}{10,862\cdot 23,139}=-0,625\text{.} \end{align*}Hodnota výberového korelačného koeficienta svedčí o stredne silnej, nepriamej závislosti medzi požadovaným množstvom a cenou výrobku. To znamená, že s rastom ceny výrobku dochádza k poklesu jeho požadovaného množstva.
Tvrdenie o štatistickej významnosti danej závislosti overíme pomocou testu o korelačnom koeficiente. Testujeme nulovú hypotézu
\[ \begin{aligned} H_0 \colon R=0 \end{aligned} \text{ oproti} \begin{aligned} H_1 \colon R \ne 0 \end{aligned} \]za pomoci testovacej štatistiky $T$; $t=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}}\frac{-0,625\sqrt{11}}{\sqrt{1-(-0,625)^2}}=-2,654$.
Kritický obor tvaru
$W=\left(-\infty;-t_{0,975}(11)\right\rangle \cup \left\langle t_{0,975}(11); \infty\right)=\left(-\infty;-2,201\right\rangle \cup \left\langle 2,201; \infty\right)$
môžeme zjednodušiť porovnaním absolútnej hodnoty testovacej štatistiky s kvantilom Studentovho rozdelenia, tj. $\vert t\vert \geq t_{0,975}(11)$. Pretože platí $\vert -2,654\vert>2,201$ ($\Rightarrow t\in W$), zamietame nulovú hypotézu na hladine významnosti $5\,\%$ a preukázali sme, že medzi požadovaným množstvom a cenou výrobku existuje štatisticky významná závislosť.
Vytvoríme dátový súbor s 2 premennými a 13 prípadmi. Pomenujeme ich X (požadované množstvo), Y (cena) a do tabuľky zapíšeme odpovedajúce hodnoty.

Postup: Statistiky – Základní statistiky/tabulky – Korelační matice; OK – 2 seznamy (obd. matice); X, Y; OK – záložka Možnosti; zaklikneme Zobrazit detailní tabulku výsledků – Výpočet.

Výberový korelačný koeficient nadobúda hodnotu $-0,6248$ a testovacia štatistika pre test o korelačnom koeficiente hodnotu $-2,6542$. Pri odpovedajúcej $p$-hodnote testu $0,0224$ a hladine významnosti $\alpha=0,05$ zamietame nulovú hypotézu o nezávislosti veličín, pretože platí $0,0224\lt 0,05$.
Príklad 3 Test významnosti korelačného koeficienta, 3.2.
Bol vykonaný hypotetický experiment zameraný na vzťah medzi pracovnou spokojnosťou a pracovným výkonom. Vzorka 42 náhodne vybraných zamestnancov hodnotila svoju vlastnú úroveň spokojnosti s prácou. Táto miera spokojnosti koreluje s hodnotením orgánov dohľadu výkonu, pričom sa dá predpokladať, že sa tieto veličiny riadia dvojrozmerným normálnym rozdelením. Otázkou je, či existuje vzťah medzi týmito dvoma mierami v celej populácii. Pomocu intervalu spoľahlivosti pre korelačný koeficient overte hypotézu o nezávislosti náhodných veličín oproti alternatíve, že sú náhodné veličiny závislé, ak ich výberový korelačný koeficient činí 0,27. [Vlastný zdroj]
Testujeme nulovú hypotézu
\[ \begin{aligned} H_0 \colon R=0 \end{aligned} \text{ oproti } \begin{aligned} H_1 \colon R \neq 0. \end{aligned} \]Poznáme hodnotu koeficienta $r=0,27$ a taktiež rozsah výberu $n=42$, ktorý je dostatočne veľký na to, aby sme pri testovaní hypotézy o nezávislosti pomocou intervalu, uvedeného v 3.2 nahradili kvantil Studentovho rozdelenia kvantilom štandardizovaného normálneho rozdelenia, tj. $t_{0,975}(40) \rightarrow u_{0,975}=1,96$. Zostavíme obojstranný interval a pozrieme sa, či obsahuje hodnotu výberového korelačného koeficienta.
\begin{align*} ( D,H ) &=\left( -\frac{ u_{0,975}}{\sqrt{ u_{0,975}+n-2}},\frac{ u_{0,975}}{\sqrt{ u_{0,975}+n-2}}\right ) = \left( -\frac{ 1,96}{\sqrt{ 1,96+40}}, \frac{ 1,96}{\sqrt{ 1,96+40}} \right)\\ & = ( -0,303;0,303) \end{align*}Keďže hodnota $0,27 \in ( -0,301;0,301) $, nezamietame na hladine významnosti $5\,\%$ nulovú hypotézu o nezávislosti náhodných veličín.
Nakoľko nie je výpočet daného intervalu implementovaný v systéme STATISTICA, využijeme ju ako inteligentnú kalkulačku.
Vytvoríme dátový súbor s 2 premennými a 1 prípadom. Prvú premennú pomenujeme D (dolná hranica) a do dlhého mena napíšeme:
$=-VNormal(0,975;0;1)/Sqrt(VNormal(0,975;0;1)+42-2)$.
Druhú premennú pomenujeme H (horná hranica) a do dlhého mena napíšeme:
$=VNormal(0,975;0;1)/Sqrt(VNormal(0,975;0;1)+42-2)$.

Získali sme hranice intervalu, ktorý má tak tvar $( -0,3026;0,3026) $. Pretože interval pokrýva hodnotu výberového korelačného koeficienta $0,27$, nezamietame nulovú hypotézu na hladine významnosti $5\,\%$.
Príklad 4 Interval spoľahlivosti pre korelačný koeficient, 3.3.
Zo základného súboru všetkých pracovníkov v určitej profesii bolo vybraných 80. Zisťujeme závislosť medzi výškou príjmu (v tis. Kč) a dĺžkou praxe (v rokoch). Pre výberový korelačný koeficient platí $r=0,72$. Za predpokladu dvojrozmernej normality určite $95\%$ obojstranný interval spoľahlivosti pre korelačný koeficient $R$. [7], str. 101
Je známy rozsah $n=80$ a koeficient $r=0,72$. Na konštrukciu intervalu spoľahlivosti pre korelačný koeficient použijeme Fisherovu Z-transformáciu výberového korelačného koeficienta, teda
\begin{align*} z= \frac{1}{2}\mathrm{ln}\left(\frac{1+r}{1-r}\right)=\frac{1}{2}\mathrm{ln}\left( \frac{1+0,72}{1-0,72}\right)&=0,908\text{.}\\ \end{align*}Zo štatistických tabuliek poznáme hodnotu kvantilu štandardizovaného normálneho rozdelenia $u_{0,975}=1,96$. Spočítame najprv interval spoľahlivosti pre $ \frac{1}{2}\mathrm{ln}\left(\frac{1+R}{1-R}\right)$:
\begin{align*} P\biggl(z -\frac{u_{1-\alpha/2}}{\sqrt{n-3}}\lt \frac{1}{2}\mathrm{ln}\left(\frac{1+R}{1-R}\right) \lt z~+\frac{u_{1-\alpha/2}}{\sqrt{n-3}} \biggr)&=1-\alpha \text{,} \\ P\biggl(0,908 -\frac{u_{0,975}}{\sqrt{77}}\lt \frac{1}{2}\mathrm{ln}\left(\frac{1+R}{1-R}\right) \lt 0,908 +\frac{u_{0,975}}{\sqrt{77}} \biggr)&=0,95 \text{,} \\ P\biggl(0,685\lt \frac{1}{2}\mathrm{ln}\left(\frac{1+R}{1-R}\right) \lt 1,131 \biggr)&=0,95\text{.} \end{align*}Podľa vzťahu $Z=\mathrm{arctgh}\,R_{12}\Rightarrow R_{12}=\mathrm{tgh}\,Z $, pričom $\mathrm{tgh}\,x=\frac{\mathrm{e}^x{}-{}\mathrm{e}^{-x}}{\mathrm{e}^x{}+{}\mathrm{e}^{-x}}$, prevedieme interval spoľahlivosti do mierky korelačného koeficienta:
\begin{align*} P\biggl(\mathrm{tgh}\,0,685\lt R \lt \mathrm{tgh}\,1,131 \biggr)&=0,95 \text{,}\\ P\biggl(\frac{\mathrm{e}^{0,685}-\mathrm{e}^{-0,685}}{\mathrm{e}^{0,685}+\mathrm{e}^{-0,685}}\lt R \lt \frac{\mathrm{e}^{1,131}-\mathrm{e}^{-1,131}}{\mathrm{e}^{1,131}+\mathrm{e}^{-1,131}} \biggr)&=0,95\text{.} \end{align*}Po vyčíslení dostávame interval $( 0,59;0,81 )$, ktorý obsahuje hodnotu korelačného koeficienta so spoľahlivosťou $95\,\%$.
Vytvoríme dátový súbor s 2 premennými a 1 prípadom, ktoré nazveme D a H. Do dlhého mena premennej D napíšeme:
$=TanH(0,5*log((1+0,72)/(1-0,72))-VNormal(0,975;0;1)/sqrt(77))$.
Do dlhého mena premennej H napíšeme:
$=TanH(0,5*log((1+0,72)/(1-0,72))+VNormal(0,975;0;1)/sqrt(77))$.

Z výstupnej tabuľky dostávame hranice $95\%$ intervalu spoľahlivosti pre korelačný koeficient. Daný interval je teda v tvare $( 0,5943;0,8114 )$.
2.spôsob: Využijeme modul „Analýza síly testu“: Statistiky – Analýza síly testu – Odhad intervalu – Jedna korelace,t-test; OK – Vyplníme Pozorované R: 0,72; Velik.vzorku (N): 80; Spolehlivost: 0,95; zaškrtneme Fisherovo Z (původ.) – Vypočítat.

Získavame totožné výsledky, hranice intervalu spoľahlivosti $0,5943$ a $0,8114$.
Príklad 5 Test hypotézy o danej hodnote korelačného koeficienta, 3.4.
U 17 rozlične degradovaných vzoriek bavlny bola stanovená relatívna viskozita, a to v roztoku ethylendiaminového komplexu s meďou (CUEN) a v alkalickom roztoku hydroxidu tetraamonmeďnatého (CUOXAN). Z týchto hodnôt boli výpočítané stupne polymerácie $DP_1$ v roztoku CUEN a $DP_2$ v roztoku CUOXAN. Predpokladajme, že pokiaľ je korelačný koeficient medzi polymeračnými stupňami nevýznamne menší než hodnota 0,85, existuje medzi výsledkami z oboch rozpúšťadiel významný lineárny vzťah. Testujte hypotézu o danej hodnote korelačného koeficienta oproti alternatíve, že je jeho hodnota menšia, ak sa hodnota výberového korelačného koeficienta rovná 0,614. [13], str. 577
Je daná konštanta $c=0,85$, koeficient $r=0,614$ a rozsah $n=17$. Testujeme nulovú hypotézu
\[ \begin{aligned} H_0 \colon R=0,85 \end{aligned} \text{ oproti } \begin{aligned} H_1 \colon R\lt 0,85\text{.} \end{aligned} \]Z hodnoty výberového korelačného koeficienta spočítame jeho Fisherovu Z-transformáciu a následne testovaciu štatistiku U:
\begin{align*} z&=\frac{1}{2}\mathrm{ln}\left(\frac{1+r}{1-r}\right)=\frac{1}{2}\mathrm{ln}\left( \frac{1+0,614}{1-0,614}\right)=0,715 \text{,}\\ u&=\biggl(z-{}\frac{1}{2}\mathrm{ln}\,\frac{1+c}{1-c}{}-{} \frac{c}{2(n-1)}\biggr)\sqrt{n-3}=\\ &=\biggl(0,715-{}\frac{1}{2}\mathrm{ln}\,\frac{1,85}{0,15}{}-{} \frac{0,85}{2\cdot16}\biggr)\sqrt{14}=-2,124\text{.} \end{align*}S kvantilom $u_{0,95}=1,645$ zostavíme ľavostranný kritický obor $W=(-\infty; -1,645\rangle$. Hodnota testovacej štatistiky $u \in W$, a preto na hladine významnosti $5\,\%$ zamietame nulovú hypotézu v prospech alternatívy, čo znamená, že závislosť medzi stupňami polymerácie nie je tak silná, ako sa predpokladalo.
Približný výpočet dostaneme postupom: Statistiky – Základní statistiky/tabulky – Testy rozdílů: r,%,průmery; OK – Rozdíl medzi dvěma korelačními koeficienty; do políčka r1 zapíšeme hodnotu koeficienta 0,614, rozsah 17 do N1, do políčka r2 zapíšeme danú konštantu 0,85 a do N2 maximálnu hodnotu 32767; zaklikneme Jednostr. – Výpočet.
Políčko N2 by malo obsahovať hodnotu „nekonečno“, v STATISTICE preto nastavujeme maximálnu možnú hodnotu ($32767$).
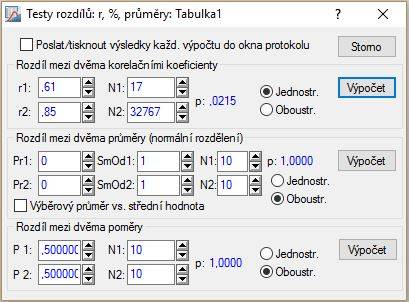
Získavame $p$-hodnotu testu rovnú $0,0215$. Na hladine významnosti $5\,\%$ zamietame nulovú hypotézu, pretože platí $0,0215\lt 0,05$.
Pre prípad presného výpočtu založenom na testovacej štatistike $U$ sme vytvorili makro $testhodnotykoef.svb$. Zdrojový kód uvádzame v prílohách (Test hypotézy o danej hodnote korelačného koeficienta – zdrojový kód).
Postupujeme: Soubor – Otevřít; vyberieme testhodnotykoef.svb – klávesou F5 spustíme makro – tabuľka Koeficient r; 0,614; OK – tabuľka Rozsah výberu; 17; OK – tabuľka Konstanta c; 0,85 – tabuľka Hladina významnosti; 0,05; OK – tabuľka Alternativna hypoteza; vyberieme Lavostranna altenativa; OK.

Z výstupnej tabuľky dostávame okrem rozsahu predovšetkým hodnotu testovacej štatistiky $-2,1230$, hodnotu kvantilu kritického oboru $1,6449$ a $p$-hodnotu $0,0169$ $\rightarrow$ $0,0169\lt 0,05$ a nulovú hypotézu zamietame na hladine významnosti $5\,\%$.
Príklad 6 Test zhody dvoch korelačných koeficientov, 3.6.
V psychologickom výskume bolo vyšetrených 12 chlapcov a 15 dievčat. V skupine chlapcov činil výberový korelačný koeficient medzi verbálnou a performačnou zložkou IQ 0,6033, v skupine dievčat činil 0,5833. Za predpokladu dvojrozmernej normality dát testujte hypotézu, že korelačné koeficienty sa nelíšia. [3], str. 232
Opäť počítame Fisherove Z-transformácie výberových korelačných koeficientov a testovaciu štatistiku U:
\begin{align*} z&=\frac{1}{2}\mathrm{ln}\left(\frac{1+r}{1-r}\right)=\frac{1}{2}\mathrm{ln}\left(\frac{1+0,6033}{1-0,6033}\right)=0,698\text{,} \\ z^*&=\frac{1}{2}\mathrm{ln}\left(\frac{1+r^*}{1-r^*}\right)=\frac{1}{2}\mathrm{ln}\left(\frac{1+0,5833}{1-0,5833}\right)=0,667 \text{,} \end{align*} \[ u=\frac{z-z^*}{\sqrt{\frac{1}{n-3}+\frac{1}{n^*-3}}}=\frac{0,698-0,667}{\sqrt{\frac{1}{9}+\frac{1}{12}}}=0,07\text{.}\]S hodnotou kvantilu štandardizovaného normálneho rozdelenia $u_{0,975}=1,96$ má kritický obor tvar $W=(-\infty;-1,96\rangle \cup \langle 1,96; \infty)$. Keďže realizácia testovacej štatistiky $0,07 \notin W$, nulovú hypotézu o rovnosti korelačných koeficientov nezamietame na asymptotickej hladine významnosti $5\,\%$.
Za pomoci systému spočítame $p$-hodnotu testu, podľa postupu z predchádzajúceho príkladu: Statistiky – Základní statistiky/tabulky – Testy rozdílů: r, %, průmery; OK – Rozdíl medzi dvěma korelačními koeficienty; r1=0,6033, N1=12, r2=0,5833 a N2=15; zaklikneme Oboustr. – Výpočet.
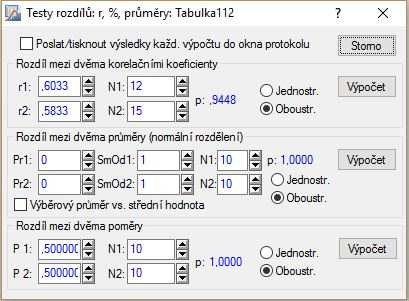
Vzhľadom na vysokú $p$-hodnotu $0,9448$, väčšiu než $\alpha=0,05$, nezamietame nulovú hypotézu o zhode korelačných koeficientov na asymptotickej hladine významnosti $5\,\%$.
Príklad 7 Test zhody $k$ korelačných koeficientov, 3.2.
Lekársky výskum sa zaoberal sledovaním koncentrácií látok $A$ a $B$ v moči pacientov trpiacich obličkovými ochoreniami. U 100 zdravých osôb činil výberový korelačný koeficient medzi koncentráciami oboch látok 0,65. U 142 osôb trpiacich ochorením $N$ činil tento výberový korelačný koeficient 0,37 a u 175 osôb trpiacich ochorením $M$ bol 0,55. Zistite, či je závislosť medzi koncentráciami látok $A$ a $B$ vo všetkých troch skupinách osôb rovnaká. [1], str. 234
K dipozícii máme tri výbery rozsahov $n_1=100$, $n_2=142$, $n_3=175$ s výberovými korelačnými koeficientami $r^1=0,65$, $r^2=0,37$, $r^3=0,55$. Na vyriešenie problému použijeme test o zhode $k$ (v našom prípade $k=3$) korelačných koeficientov:
\[ \begin{aligned} H_0 \colon R_1=R_2=R_3 \end{aligned} \text{ oproti } \begin{aligned} H_1 \colon \text{„aspoň dva koeficienty sú rozdielne“}\text{.} \end{aligned} \]Pre každý z výberov vypočítame Fisherovu Z-transformáciu:
\begin{align*} z_1&=\frac{1}{2}\mathrm{ln}\left(\frac{1+r^1}{1-r^1}\right)=\frac{1}{2}\mathrm{ln}\left( \frac{1+0,65}{1-0,65}\right)=0,775\text{,}\\ z_2&=\frac{1}{2}\mathrm{ln}\left(\frac{1+r^2}{1-r^2}\right)=\frac{1}{2}\mathrm{ln}\left( \frac{1+0,37}{1-0,37}\right)=0,388 \text{,}\\ z_3&=\frac{1}{2}\mathrm{ln}\left(\frac{1+r^3}{1-r^3}\right)=\frac{1}{2}\mathrm{ln}\left( \frac{1+0,55}{1-0,55}\right)=0,618 \text{.} \end{align*}Platí $n=n_1+n_2+n_3=417$. Spočítame koeficient $b$ a následne testovaciu štatistiku $\chi^2$:
\begin{align*} b&=\small\frac{1}{n-3k}\sum_{i=1}^k(n_i-3)z_i=\frac{1}{417-9}(97\cdot0,775+139\cdot0,388+172\cdot0,618)=0,577 \text{,} \\ \chi^2&=\small\sum_{i=1}^k(n_i-3)(Z_i-b)^2=(97\cdot0,198^2+139\cdot(-0,189)^2+172\cdot0,041^2)=9,052 \text{.} \end{align*}Pre $\alpha=0,05$ a kvantil $\chi_{0,95}^2(2)=5,99$ je kritický obor $W=\left\langle 5,99; \infty \right)$. Pretože štatistika $\chi^2 \in W$, na asymptotickej hladine významnosti $5\,\%$ zamietame nulovú hypotézu, že závislosť medzi koncentráciami látok A, B je vo všetkých troch skupinách rovnaká. Tukeyovým testom preto zistíme, medzi ktorými skupinami osôb existuje štatisticky významný rozdiel. S tabelovanou hodnotou $q_{k,\infty}(\alpha)=q_{3,\infty}(0,05)=3,31$ spočítame nerovnosti
\begin{align*} \vert z_i-z_j \vert &\geq q_{k,\infty}(\alpha)\cdot \sqrt{\frac{1}{2}\left(\frac{1}{n_i-3}+\frac{1}{n_j-3}\right)}\text{;}\\ \vert 0,775-0,388 \vert &\geq 3,31\cdot \sqrt{\frac{1}{2}\left(\frac{1}{97}+\frac{1}{139}\right)} \rightarrow \vert 0,387 \vert \geq 0,310 \text{,}\\ \vert 0,775-0,618 \vert &\geq 3,31\cdot \sqrt{\frac{1}{2}\left(\frac{1}{97}+\frac{1}{172}\right)} \rightarrow \vert 0,157 \vert \ngeq 0,297\text{,}\\ \vert 0,388-0,618 \vert &\geq 3,31\cdot \sqrt{\frac{1}{2}\left(\frac{1}{139}+\frac{1}{172}\right)} \rightarrow \vert -0,230 \vert \ngeq 0,267 \text{.} \end{align*}Nerovnosť platí iba v prvom prípade, čím sme dokázali, že medzi zdravými osobami a osobami trpiacimi chorobou $N$ existuje na hladine $0,05$ štatisticky významný rozdiel, pričom ostatné rozdiely sú štatisticky nevýznamné.
Systém STATISTICA nemá implementované testy pre tento typ úlohy, preto sme vytvorili makrá, testzhodykkoef.svb a Tukeytest.svb, odpovedajúce testu zhody $k$ korelačných koeficientov a Tukeyovmu testu. Zdrojové kódy uvádzame v prílohách (Test hypotézy o danej hodnote korelačného koeficienta, Test zhody k korelačných koeficientov).
Pred spustením makier vytvoríme dátovú tabuľku s 2 premennými a 3 prípadmi. Premenné nazveme K pre koeficienty, N pre rozsahy a zapíšeme odpovedajúce hodnoty.

Test zhody k korelačných koeficientov: Soubor – Otevřít; vyberieme testzhodykkoef.svb – klávesou F5 spustíme makro – tabuľka Výber premenných; z prvého zoznamu vyberieme K, z druhého N; OK – tabuľka Hladina významnosti; 0,05; OK.

Vo výslednej tabuľke nájdeme počet korelačných koeficientov $3$, hodnotu testovacej štatistiky $9,0518$, hodnotu kvantilu kritického oboru $5,9915$ a $p$-hodnotu testu $0,0108$. $P$-hodnota je menšia ako hladina významnosti $0,05$, podľa čoho zamietame nulovú hypotézu na hladine významnosti $5\,\%$ v prospech alternatívy.
Tukeyov test: Soubor – Otevřít; vyberieme Tukeytest.svb – klávesou F5 spustíme makro – tabuľka Výber premenných; z prvého zoznamu vyberieme K, z druhého N; OK – tabuľka Tabelovana hodnota; 3,31; OK.

Výsledná tabuľka Tukeyovho testu zobrazuje maticu rozdielov Fisherových Z-transformácií, z ktorých sú zvýraznené tie hodnoty, pre ktoré platí nerovnosť testu. Podľa indexov $i$, $j$ vidíme, že štatisticky významný rozdiel je medzi Fisherovými transformáciami $z_1$ a $z_2$, tj. medzi skupinami zdravých osôb a osôb trpiacimi chorobou $N$.
Makro Tukeytest.svb vytvára taktiež tabuľku kritických hodnôt testu označenú tabC, ktorej výpis je potlačený zakomentovaným príkazom tabC.Visible=True. V prípade, že chce čitateľ tabuľku zobraziť, stačí v zdrojovom kóde tento príkaz odkomentovať, tj. 'tabC.Visible=True nahradíme
tabC.Visible=True.
Príklad 8 Test významnosti Spearmanovho korelačného koeficienta, 3.7.
Bolo sledovaných 10 poslucháčov 2. ročníka VŠE. Na základe psychologického vyšetrenia boli títo poslucháči zoradení podľa nervovej lability (čím bol poslucháč labilnejší, tým dostal vyššie poradie $R_i$). Okrem toho sledovaní poslucháči dostali poradie $Q_i$ na základe výsledkov v štatistike (najlepší poslucháč dostal poradie 1). Výsledky sú uvedené v tabuľke. Zistite, či je nervová labilita nezávislá od výsledkov v štatistike. [8], str. 90
| $R_i$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| $Q_i$ | 9 | 3 | 8 | 5 | 4 | 2 | 10 | 1 | 7 | 6 |
Keďže máme k dispozícii poradia 10 poslucháčov, budeme testovať poradovú nezávislosť s nulovou hypotézou
\[ \begin{aligned} H_0 \colon R_s=0 \end{aligned} \text{ oproti } \begin{aligned} H_1 \colon R_s \ne 0 \end{aligned} \]a ako testovacie kritérium použijeme Spearmanov korelačný koeficient $r_s$. Na jeho výpočet určíme najprv rozdiely $R_i -Q_i$:
| $R_i-Q_i$ | $-8$ | $-1$ | $-5$ | $-1$ | $1$ | $4$ | $-3$ | $7$ | $2$ | $4$ |
|---|
Pri hladine významnosti $\alpha=0,05$, rozsahu $n=10$ a tabuľkovej hodnote $r_{s,0,975}(10)=0,6364$ má kritický obor tvar $W=\bigl( -1; -0,6364 \bigr\rangle \cup \bigl\langle 0,6364; 1 \bigr)$. Hodnota Spearmanovho koeficienta korelácie $-0,127 \notin W$, a preto nulovú hypotézu o (poradovej) nezávislosti nervovej lability poslucháčov a výsledkov v štatistike nezamietame na hladine významnosti $5\,\%$.
Vytvoríme dátový súbor s 2 premennými $R_i$, $Q_i$ a 10 prípadmi, kde zapíšeme odpovedajúce poradia.

Spearmanov koeficient korelácie: Statistiky – Neparametrická statistika – Korelace (Spearman, Kendallovo tau, gama); OK – Proměnné; Ri, Qi; OK – Spearman.R.

Hodnotu Spearmanovho koeficienta korelácie porovnáme s kritickou tabelovanou hodnotou $r_{s,0,975}(10)=0,6364 \rightarrow \vert -0,1273\vert \lt 0,6364 \rightarrow$ nulovú hypotézu o (poradovej) nezávislosti nezamietame.
Príklad 9 Test významnosti Spearmanovho korelačného koeficienta, 3.7.
V tabuľke je zaznamenaný percentuálny podiel ľudí s pracovnou zmluvou na dobu určitú (veličina $X$) a percentuálny podiel nezamestnaných ľudí (veličina $Y$) v krajinách Európskej únie. Pomocou vhodného koeficienta určite a otestujte závislosť medzi pozorovanými veličinami $X$, $Y$. [11], str. 400
| Štát | $x_{i}$ | $y_{i}$ |
|---|---|---|
| Belgicko | 8,6 | 7,5 |
| Bulharsko | 5,2 | 6,9 |
| Česká republika | 8,6 | 5,3 |
| Dánsko | 8,7 | 3,7 |
| Nemecko | 14,6 | 8,4 |
| Estónsko | 2,1 | 4,7 |
| Írsko | 7,3 | 4,5 |
| Grécko | 10,9 | 8,3 |
| Španielsko | 31,7 | 8,3 |
| Francúzsko | 14,4 | 8,3 |
| Taliansko | 13,2 | 6,1 |
| Cyprus | 13,2 | 3,9 |
| Lotyšsko | 4,2 | 6 |
| Litva | 3,5 | 4,3 |
| Luxembursko | 6,8 | 4,7 |
| Maďarsko | 7,3 | 7,4 |
| Malta | 5,2 | 6,4 |
| Holandsko | 18,1 | 3,2 |
| Rakúsko | 8,9 | 4,4 |
| Poľsko | 28,2 | 9,6 |
| Portugalsko | 22,4 | 8 |
| Rumunsko | 1,6 | 6,4 |
| Slovinsko | 18,5 | 4,8 |
| Slovensko | 5,10 | 11,10 |
| Fínsko | 15,9 | 6,9 |
| Švédsko | 17,5 | 6,1 |
| Anglicko | 5,8 | 5,3 |
V tomto prípade typ dát nerozhoduje o postupe riešenia úlohy, rozhodneme tak ale podľa splneného resp. nesplneného predpokladu dvojrozmernej normality.
Podľa tabuľky testov jednorozmernej normality zamietame normalitu náhodnej veličiny $X$. Porušenie normality naznačuje aj dvojrozmerný bodový diagram, a preto v rámci korektnosti použijeme Spearmanov korelačný koeficient, aj keď by takéto mierne odchýlenie od normality významne neovplynilo výsledok pri použití Pearsonovho (výberového) korelačného koeficienta.


Spočítame teda poradovú závislosť. Kedže máme k dispozícii realizácie náhodných veličín, určíme najprv ich poradové čísla (najnižšia hodnota má poradové číslo 1). Pre prehľadnosť a uľahčenie výpočtu Spearmanovho koeficienta $r_s$ zostavíme najskôr tabuľku obsahujúcu realizácie náhodných veličín, ich poradia a druhú mocninu rozdielu týchto poradí.
| $x_{i}$ | $y_{i}$ | $R_{i}$ | $Q_{i}$ | $(R_{i}-Q_{i})^2$ |
|---|---|---|---|---|
| 8,6 | 7,5 | 12,5 | 20 | 56,3 |
| 5,2 | 6,9 | 6,5 | 17,5 | 121 |
| 8,6 | 5,3 | 12,5 | 10,5 | 4 |
| 8,7 | 3,7 | 14 | 2 | 144 |
| 14,6 | 8,4 | 20 | 25 | 25 |
| 2,1 | 4,7 | 2 | 7,5 | 30,3 |
| 7,3 | 4,5 | 10,5 | 6 | 20,3 |
| 10,9 | 8,3 | 16 | 23 | 49 |
| 31,7 | 8,3 | 27 | 23 | 16 |
| 14,4 | 8,3 | 19 | 23 | 16 |
| 13,2 | 6,1 | 17,5 | 13,5 | 16 |
| 13,2 | 3,9 | 17,5 | 3 | 210,3 |
| 4,2 | 6 | 4 | 12 | 64 |
| 3,5 | 4,3 | 3 | 4 | 1 |
| 6,8 | 4,7 | 9 | 7,5 | 2,3 |
| 7,3 | 7,4 | 10,5 | 19 | 72,3 |
| 5,2 | 6,4 | 6,5 | 15,5 | 81 |
| 18,1 | 3,2 | 23 | 1 | 484 |
| 8,9 | 4,4 | 15 | 5 | 100 |
| 28,2 | 9,6 | 26 | 26 | 0 |
| 22,4 | 8 | 25 | 21 | 16 |
| 1,6 | 6,4 | 1 | 15,5 | 210 |
| 18,5 | 4,8 | 24 | 9 | 225 |
| 5,1 | 11,1 | 5 | 27 | 484 |
| 15,9 | 6,9 | 21 | 17,5 | 12,3 |
| 17,5 | 6,1 | 22 | 13,5 | 72,3 |
| 5,8 | 5,3 | 8 | 10,5 | 6,3 |
Táto nízka hodnota koeficienta $0,225$ naznačuje pomerne slabú poradovú závislosť medzi veličinami. V nasledujúcom kroku otestujeme, či skutočne existuje.
Staviame nulovú hypotézu
\[ \begin{aligned} H_0 \colon R_s=0 \end{aligned} \text{ oproti } \begin{aligned} H_1 \colon R_s \ne 0. \end{aligned} \]Vzhľadom na veľkosť rozsahu výberu $n=27>20$ použijeme testovaciu štatistiku $T$:
\[ t=\frac{r_s\sqrt{n-2}}{\sqrt{1-r_s^2}}=\frac{0,225\cdot 5}{\sqrt{1-0,0506}}=1,155\text{.}\]V tabuľkách nájdeme hodnotu kvantilu Studentovho rozdelenia $t_{0,975}(25)=2,0595$ a zostrojíme kritický obor pre daný test $W=(-\infty; -2,0595\rangle \cup \langle 2,0595; \infty )$. Hodnota testovacej štatistiky $1,155$ neleží v kritickom obore $W$, a preto na hladine významnosti $5\,\%$ nezamietame nulovú hypotézu. Nepreukázali sme, že medzi veličinami existuje závislosť.
Postup riešenia je takmer identický ako v minulom príklade. Vytvoríme dátový súbor s 2 premennými a 27 prípadmi určujúcimi realizácie veličín $X$, $Y$. Nie je potrebné zadávať poradové čísla, tie si STATISTICA pri výpočte určí automaticky (Z dôvodu rozsiahleho počtu pozorovaní tabuľku neuvádzame.).
Postup: Statistiky – Neparametrická statistika – Korelace (Spearman, \ldots);OK --Vytvoriť; Detailní report – Proměnné; X, Y; OK – Spearman.R.

Z výstupnej tabuľky nás predovšetkým zaujíma $p$-hodnota testu rovná $0,2623$, čo je hodnota väčšia ako $\alpha=0,05$, a preto nulovú hypotézu nezamietame na hladine významnosti $5\,\%$.