Celý náš život je spojený jak se symetrií, tak s asymetrií, a to pokud mluvíme například i o našem vzhledu nebo chování. Pojem symetrie je však nejvíc vázán k estetice jako filozoficko-umělecké zobrazení, které se reálně manifestuje i v přírodě. Tímto na první pohled ne vždy viditelným zobrazením se symetrie stává součástí biologie. Když objektivně uvažujeme nad propojením symetrie s vědami, jako první se logicky nabízí matematika. Od matematické teorie grup se plynule můžeme přesunout k chemii, kde symetrie tvoří podstatnou část různých vědních disciplín, jak v anorganické, organické, tak i fyzikální chemii. Samozřejmě fyzika není žádnou výjimkou. Symetrie fyzikálních zákonů a teorií ale nemusí být tak snadno postřehnutelná pro nás nefyziky.
Symetrie daného objektu je dána prvky jeho základní struktury. Tak jako symetrie jednoho šestiúhelníku nám prozrazuje symetrii celé plástve ze včelího úlu, tak symetrie uspořádání iontů, atomů nebo molekul prozrazuje stavbu hmoty. Pochopení zákonitostí a principů, které tvarují rozmanité struktury hmoty nám poskytuje další možnosti při výrobě nových materiálů stejně, jako využití již existujících. Ve větší nebo menší míře můžeme pozorovat v hmotě vnitřní řád. Zachování pravidelnosti struktury látek se může různit v závislosti na vzdálenosti (sklo), směru (tekuté krystaly) nebo hloubce (povrchy a mezifáze) struktury.
Operace symetrie jsou operace, které když provedeme, výsledný stav molekuly je nerozeznatelný od výchozí situace. Změnou polohy určitých částí molekuly dostaneme stejné zobrazení. Části nebo body, které nezmění polohu během provedení operace symetrie, leží v prvku symetrie. Rozlišujeme pět operací symetrie a každé náleží prvek symetrie, vůči kterému se provádí. Za operace symetrie považujeme rotaci, zrcadlení a inverzi. Prvek symetrie, vzhledem ke kterému se operace symetrie provádí, může být bod, přímka nebo rovina. (1)
Tabulka č. 1: Přehled prvků a operací symetrie
Prvky symetrie |
Operace symetrie |
||
|---|---|---|---|
E | Celá molekula (prostor) | E | Identita |
Cn | Rotační osa | Cn | Vlastní rotace o úhel 2π/n |
σ | Rovina symetrie | σ | Zrcadlení v rovině kolmé k ose otáčení |
i | Střed symetrie | i | Inverze vůči středu symetrie |
Sn | Rotačně-reflexní osa | Sn | Nevlastní rotace |
Identita: Operace totožnosti, při které se každý bod zobrazuje sám na sebe. Operace identity nic nemění, všechny atomy jakoby zůstanou na stejném místě. Tahle operace představuje rotaci o 360° kolem jakékoli osy, která přechází kterýmkoliv bodem. Prvkem symetrie je celý prostor molekuly. Všechny molekuly mají operaci totožnosti, avšak pokud to je jediná operace, kterou mají, jsou označovány jako asymetrické, například bromchlorfluoromethan.
Vlastní rotace: Prvkem symetrie této operace je n- četná osa symetrie, kolem které se může molekula otočit o úhel 360°/n tak, aby byla poloha molekuly stejná jako výchozí poloha.
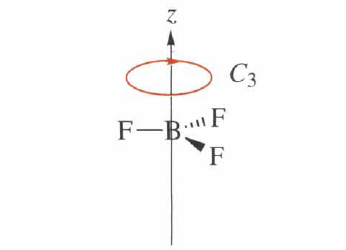
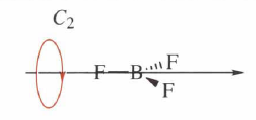
Zrcadlení: Prvkem symetrie zrcadlení je rovina symetrie, která vytváří zrcadlový obraz každého atomu tak, aby byla nová poloha molekuly nerozlišitelná od polohy výchozí. Tato rovina se značí 𝜎 a pouze atomy, které leží na této rovině, zůstávají na svém místě. Rozlišujeme tři typy rovin symetrie a to horizontální, vertikální a dihedrální (diagonální). Vertikální rovina symetrie obsahuje hlavní osu symetrie a horizontální rovina je na hlavní osu kolmá. Diagonální rovina je umístěná mezi dvěma C2 osami.
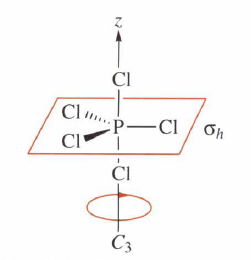
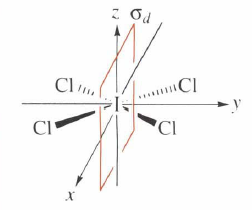
Inverze: Střed symetrie je bod, který rozděluje přímku procházející tímto bodem a původním atomem na dvě poloviny. Nový atom se po operaci inverze zobrazí na druhé polovině přímky, než je původní atom, a to ve stejné vzdálenosti od tohoto bodu, aniž by byla nová poloha molekuly rozlišitelná od polohy výchozí. Tento bod se značí 𝑖. Na svém místě přitom zůstává pouze atom ležící na středu symetrie. Ostatní atomy například se souřadnicemi x, y, z, se přesunou na souřadnice -x, -y, -z.
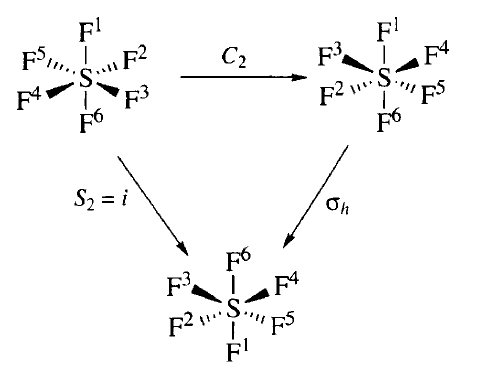
Nevlastní rotace: Tato operace symetrie se skládá ze dvou operací provedených po sobě. Provedeme zrcadlení v rovině kolmé k ose otočení a otáčení kolem dané osy o úhel 360°/𝑛, tak aby nová poloha molekuly byla nerozlišitelná od polohy výchozí.
V rámci systematické klasifikace molekul nebo krystalů, používáme matematicky přesně definované skupiny nazývané bodové grupy symetrie. Bodová grupa je množinou prvků symetrie, a její operace ponechávají alespoň jeden bod tělesa nepohyblivý v prostoru. Rozlišujeme dvě soustavy označení, pro molekuly je to Schönfliesova a pro krystaly je to soustava Hermann-Mauguinova.
Tabulka č. 2: Soustavy označení bodových grup pro molekuly a krystaly (3)
| Schönfliesova soustava | Hermann-Mauguinova soustava | Schönfliesova soustava | Hermann-Mauguinova soustava |
|---|---|---|---|
| C1 | 1 | C3i = S6 | − 3 |
| Ci = S2 | − 1 | D3 | 32 |
| C2 | 2 | C3v | 3m |
| CS = S1 | m | D3d | −3m |
| C2h | 2/m | C6 | 6 |
| C2v | 2mm | C3h | − 6 |
| D2 | 222 | D6 | 622 |
| D2h | mmm | D3h | −6m |
| C4 | 4 | C6h | 6/m |
| S4 | − 4 | C6v | 6mm |
| D4 | 442 | D6h | 6/mmm |
| C4v | 4mm | T | 23 |
| C4h | 4/m | Th | m−3 |
| D2d | −42m | Td | −43m |
| D4h | 4/mm | O | 432 |
| C3 | 3 | Oh | m−3m |
Hermann-Mauguinova soustava se používá na vyjádření prvků souměrnosti, a jejich pozici v prostoru. Pro symboly je důležitým aspektem směr, a existuje 32 kombinací symbolů. Osy se vyjadřují číslem, které vyjadřuje četnost dané osy. Roviny souměrnosti se značí písmenem m, které udává, že kolmo na daný směr se nachází rovina souměrnosti. Operace inverze a prvek střed symetrie se vyjadřuje symbolem číslem 1 s čárou nad číslem. Číselné symboly se používají i pro nevlastní rotace. (1)
Tabulka č. 3: Porovnání Hermann-Marguinovy soustavy a Schönfliesovy soustavy
| Hermann-Mauguinova soustava | Schönfliesova soustava | Prvky symetrie | Operace symetrie |
|---|---|---|---|
| 1, 2, 3, 4, 6 | C1, C2, C3, C4, C6 | Rotační osa | Vlastní rotace |
| m | σ | Rovina symetrie | Zrcadlení |
| − 1 |
i | Střed symetrie | Inverze |
| − 3 − 4 − 6 |
S3, S4, S6, | Rotačně-reflexní osa | Nevlastní rotace |
Tabulka č. 4: Vybrané bodové grupy s prvky symetrie a příklady jednotlivých molekul
| Bodové grupy | Prvky symetrie | Molekula |
|---|---|---|
| C1 | E | CHClBrI |
| Cs | E,σ | BFClBr |
| C2 | E, C2 | H2O2 |
| C2v | E, C2, σv, σv´ | H2O |
| C3v | E, C3, , 3σ | NH3 |
| C∞v | E, C∞, ∞σ | HCl |
| E, 3C2, 3σ, i | C2F4 | |
| D4h | E, C4, , C2, , , i, S4, , σ, 2σ´,2σ´´ | XeF4 |
| D∞h | E, C∞, S∞, ∞C2, ∞σ, σ´, i | C2H2 |
| Td | E, 4C3, 4, 3C2, 3S4, 3, 6σ | CH4 |
V rámci systematické klasifikace molekul nebo krystalů, používáme matematicky přesně definované skupiny nazývané bodové grupy symetrie. Bodová grupa je množinou prvků symetrie, a její operace ponechávají alespoň jeden bod tělesa nepohyblivý v prostoru. Rozlišujeme dvě soustavy označení, pro molekuly je to Schönfliesova a pro krystaly je to soustava Hermann-Mauguinova.
Hermann-Mauguinova soustava se používá na vyjádření prvků souměrnosti, a jejich pozici v prostoru. Pro symboly je důležitým aspektem směr, a existuje 32 kombinací symbolů. Osy se vyjadřují číslem, které vyjadřuje četnost dané osy. Roviny souměrnosti se značí písmenem m, které udává, že kolmo na daný směr se nachází rovina souměrnosti. Operace inverze a prvek střed symetrie se vyjadřuje symbolem číslem 1 s čárou nad číslem. Číselné symboly se používají i pro nevlastní rotace. (1)
Molekuly, které patří do bodové grupy C1 jsou asymetrické molekuly, které mají jen jediný prvek symetrie, identitu E.
Pokud má molekula kromě identity pouze střed symetrie i, patří do bodové grupy Ci. U bodové grupy Ci se můžeme někdy setkat i s označením S2, protože operace i je totožná s operací S2. Příkladem je 1,2-dibrom-1,2-dichlorethan v nezákrytové konformaci nebo kyselina mezo-vinná .
Do bodové grupy Cs patří molekuly, které mají vedle identity pouze jednu rovinu symetrie 𝜎. Nelze určit, zda se jedná o rovinu symetrie horizontální nebo vertikální, proto se u bodové grupy Cs setkáme i s označením C1h nebo C1v. Příkladem je chinolin a 1-brom-2-chlorethen. (4)
Molekuly, které mají pouze jednu 𝑛-četnou rotační osu symetrie a identitu patří do bodových grup Cn. Příkladem může být molekula peroxidu vodíku, která patří do bodové grupy C2, protože má dvoučetnou rotační osu.
Bodová grupa Cnv zahrnuje molekuly, které mají 𝑛-četné rotační osy symetrie a navíc 𝑛-vertikální roviny symetrie. Do této grupy náleží molekula vody, která má dvoučetnou rotační osu a dvě vertikální roviny symetrie.
Do bodové grupy C∞v patří všechny lineární molekuly bez středu symetrie. Dané molekuly jsou heteronukleární a dvou nebo víceatomové, mají ∞-četnou rotační osu symetrie a nekonečně mnoho vertikálních rovin symetrie. Příkladem je molekula HBr nebo HCN. (4)
Molekuly, které patří do bodových grup Cnh mají 𝑛-četné rotační osy symetrie a ještě horizontální rovinu symetrie. Příkladem může být molekula kyseliny trihydrogenborité, která patří do bodové grupy C3h. Pokud je četnost rotačních os sudá, má molekula i střed symetrie. Například molekula trans-1,2-dichlorethenu má i střed symetrie a patří do bodové grupy C2h.
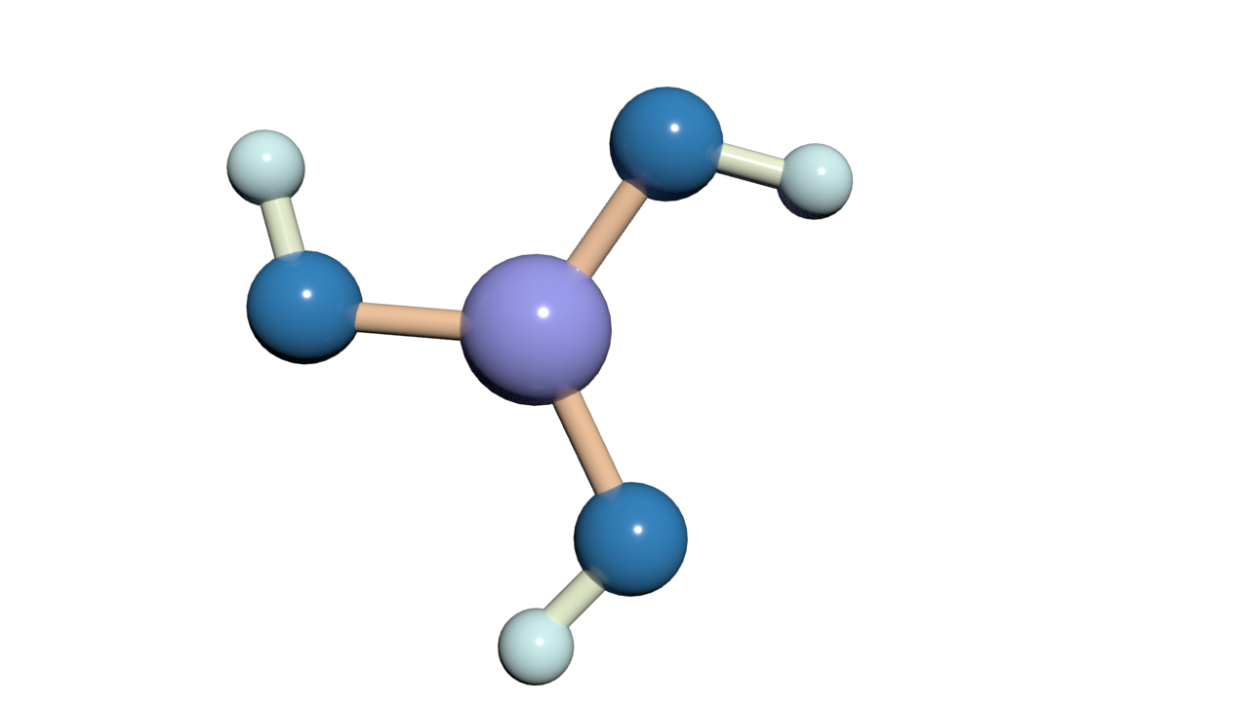
Molekuly, které patří do bodových grup Dn mají 𝑛-četnou hlavní rotační osu symetrie a 𝑛-dvoučetných rotačních os symetrie na ni kolmých.
Do bodových grup Dnh patří molekuly, které mají rotační osy symetrie bodové grupy Dn a ještě horizontální rovinu symetrie a 𝑛-vertikálních rovin symetrie, v nichž dvoučetné rotační osy symetrie leží. Například molekula fluoridu boritého náležící do grupy D3h. Pokud je počet 𝑛-vertikálních rovin sudý, má molekula i střed symetrie. Příklad může být molekula 1,4-dibrombenzenu, která patří do bodové grupy D2h.
Do bodových grup D∞h patří všechny lineární molekuly se středem symetrie. Dané molekuly jsou například homonukleární a dvouatomové a mají ∞-četnou hlavní rotační osu symetrie, nekonečně mnoho dvoučetných rotačních os symetrie na ni kolmých, horizontální rovinu symetrie a nekonečně mnoho vertikálních rovin symetrie, v nichž leží dvoučetné rotační osy symetrie.
Pokud má molekula kromě rotačních os symetrie bodové grupy Dn ještě
i 𝑛-dihedrálních rovin symetrie, patří do bodových grup Dnd. Pokud je počet 𝑛-dihedrálních rovin symetrie lichý, má molekula i střed symetrie. Příklad může být molekula allenu, která patří do bodové grupy D2d a má dvoučetnou hlavní rotační osu, dvě další dvoučetné rotační osy na ni kolmé a dvě vertikální roviny symetrie. (4)
Molekuly, které mají 𝑛-četnou rotační osu symetrie a s ní totožnou 2𝑛-četnou nevlastní rotační osu symetrie, patří do bodových grup S2n. Příklad může být molekula tetrabromneopentanu, která patří do bodové grupy S4. Pokud je počet 𝑛 lichý, má molekula i střed symetrie.
Molekuly, které mají více než jednu rotační osu symetrie s četností větší než 2 patří do kubických bodových grup symetrie. Kubické bodové grupy symetrie dělíme na tetraedrické bodové grupy T, Td a Th, oktaedrické bodové grupy O a Oh a ikosaedrické bodové grupy I a Ih. Do bodové grupy T patří molekuly, které mají čtyři trojčetné a tři dvoučetné rotační osy symetrie.
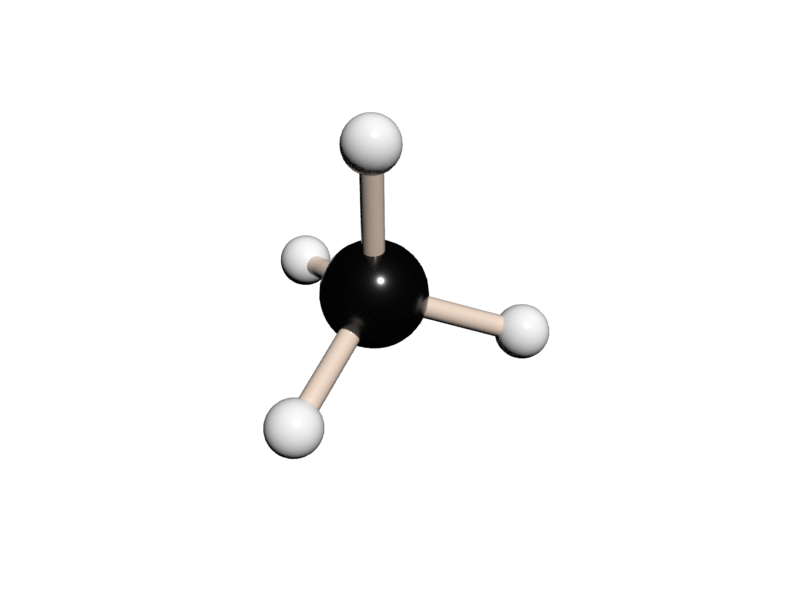
Z teorie grup vyplývá, že operace symetrie můžeme skládat. Složením dvou operací symetrie, které nejsou identické, dostaneme novou operaci symetrie. Pokud spojíme stejné operace symetrie, dostaneme operaci identity E, nebo v případě rotačních os spojením stejných vedlejších os získáme osu hlavní. Příkladem může být spojení dvou os a dostáváme hlavní osu C3 u molekuly amoniaku. (4)
Tabulka č. 5: Multiplikační tabulka znázorňující operace symetrie molekuly vody (4)
| C2v | První operace | |||
| Druhá operace | E | C2 | σv | σv´ |
| E | E | C2 | σv | σv´ |
|---|---|---|---|---|
| C2 | C2 | E | σv´ | σv |
| σv | σv | σv´ | E | C2 |
| σv´ | σv´ | σv | C2 | E |
Tabulka č. 6: Multiplikační tabulka znázorňující operace symetrie molekuly amoniaku (4)
| C3v | První operace | |||||
| Druhá operace | E | C3 | C32 | σv | σv´ | σv´´ |
| E | E | C3 | C32 | σv | σv´ | σv´´ |
| C3 | C3 | C32 | E | σv´´ | σv | σv´ |
| C32 | C32 | E | C3 | σv´ | σv´´ | σv |
| σv | σv | σv´ | σv´´ | E | C3 | C32 |
| σv´ | σv´ | σv´´ | σv | C32 | E | C3 |
| σv´´ | σv´´ | σv | σv´ | C3 | C32 | E |
Symetrie ovlivňuje mnohé vlastnosti molekul, v první řadě je to elektronová struktura a vazebné poměry molekul. Elektronová struktura atomů a molekul souvisí kromě symetrie i s degenerací energetických hladin. Když hovoříme o degenerovaných orbitalech, znamená to, že mají stejnou energii. Elektrony, které jsou ve stejné energetické hladině, mají stejné hlavní kvantové číslo n i vedlejší kvantové číslo l. Liší se jenom v magnetickém kvantovém čísle m, které udává orientaci orbitalu v prostoru. Vždy máme degenerované tři p orbitaly, pět d orbitalů a sedm f orbitalů. S rostoucí symetrií se zvyšuje stupeň degenerace. To znamená, že čím vyšší je stupeň symetrie, tím větší bude jejich degenerace. Rovněž platí, že když se hladiny energie rozštěpí, klesá molekulární symetrie. (5)
Pouhá znalost symetrie bodové grupy molekuly nám umožňuje vyvodit informace o vnitřním pohybu dané molekuly. Translační, rotační a vibrační pohyby molekul vyjadřují stupně volnosti molekul. Translační pohyb dává molekulám tři stupně volnosti odpovídající prostorovým souřadnicím x, y, z. V případě rotačního a vibračního pohybu jsou stupně volnosti závislé na symetrii dané molekuly. Stupně volnosti při rotačním pohybu jsou tři. Avšak pro lineární molekuly máme jenom dva, jelikož při třetím rotačním pohybu se nemění poloha atomů. Při vibračním pohybu je počet stupňů volnosti 3N-6 nebo pro lineární molekuly 3N-5. N představuje počet atomů v molekule. Vibrace je změna relativní polohy atomů molekuly při jakékoli teplotě beze změny polohy molekulárního těžiště. Pokud jde o molekulární geometrii, důsledkem vibrace je neustále se měnící velikosti délky vazeb a vazebných úhlů. Vibrační pohyby molekul mají využití v IR spektroskopii a Ramanově spektroskopii (5)
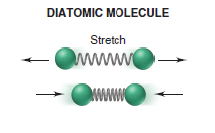
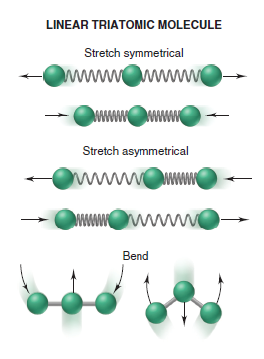
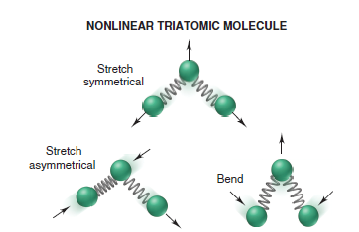
Mnoho chemických procesů a stavů závisí na elektronové struktuře atomů a molekul. Tvorba molekul z atomů, jejich chování a reaktivita závisí na elektronické struktuře. Z elektronové struktury a symetrie lze hodně vyčíst například možnost vytvoření vazby nebo průběh chemickým reakcí a jiné. Aplikováním pravidel symetrie můžeme vysvětlit a předpovědět chemické reakce. Chemická reakce představuje víc než jen změny v elektronové struktuře. Rozbití vazeb a formování nových je doprovázeno přestavbami a změnou vibrací molekul. (5)
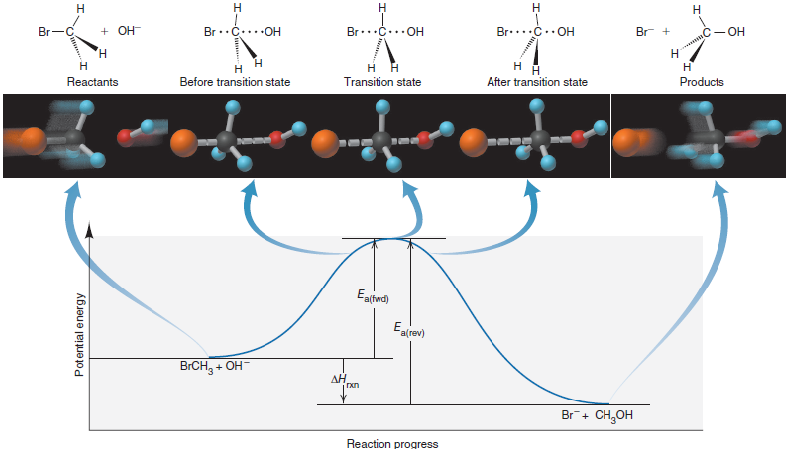
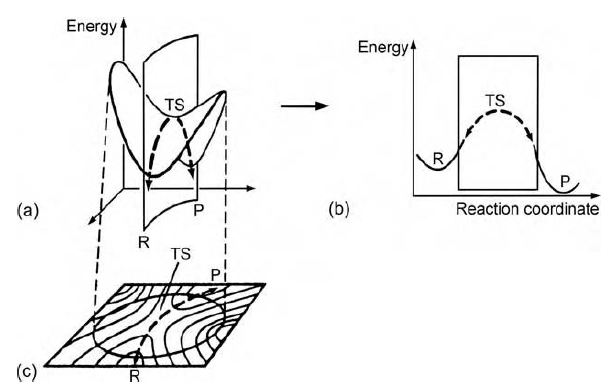
Tranzitní stav má strategický význam v oblasti chemické reaktivity. Ovlivňuje směr i řád chemické reakce, nakolik je umístěn v oblasti nejvyššího energetického bodu mezi reaktanty a produkty. Životnost tranzitního stavu je méně
než 10-12 s. Změny pozice jednotlivých atomů v průběhu reakce popisuje reakční koordináta. (5)
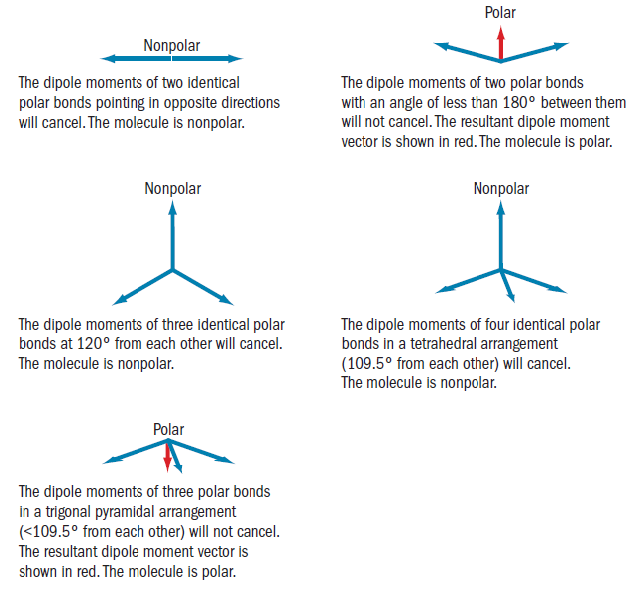
Dipólový moment jako měřitelná fyzikální veličina se při provedení operací symetrie nesmí lišit. Jak vektorová veličina se musí nacházet ve všech prvcích symetrie, proto molekula se středem symetrie nemá dipólový moment. Molekuly s operacemi vlastní symetrie Cn mají nenulový dipólový moment.
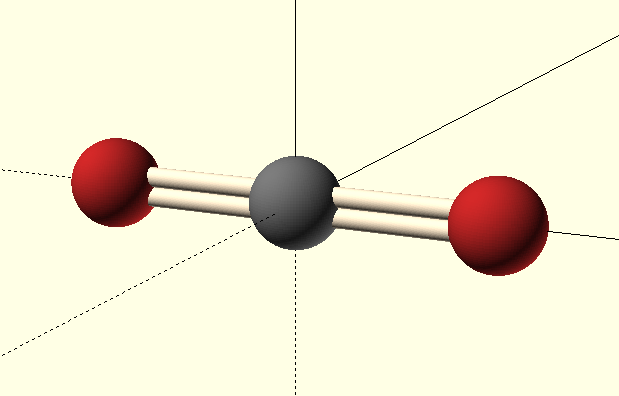
Chiralita je optická otáčivost molekul. Molekula je chirální pokud nemůže být ztotožněná se svým zrcadlovým obrazem. Molekuly mající operaci Sn (zrcadlení s rotačně reflexní osou) S1 (rovinu) nebo S2 (střed symetrie) jsou achirální.