Alternativní rozdělení: $A(p)$
Používá se v případech, když sledujeme výskyt určité náhodné události. Náhodná veličina $X\sim A(p)$ nabývá hodnoty 0 nebo 1. Hodnotu 1 s pravděpodobností $p$ přiřadíme náhodné veličině, jestli při náhodném pokusu nastala námi sledovaná událost, neboli jinak řečeno "úspěch". Naopak, náhodné veličině přiřadíme hodnotu 0 s pravděpodobností $1-p$, jestliže námi sledovaná událost nenastala. Obor hodnot obsahuje jenom dva prvky: $M=\{0,1\}$.
Pravděpodobnostní funkce je tvaru:
\begin{equation}
p(x) =
\begin{cases}
1-p &\text{pro $x=0$}\\
p &\text{pro $x=1$} \\
0 &\text{jinak}
\end{cases}\tag{1.5}
\end{equation}
Ekvivalentní zápis:
\begin{equation}
p(x) =
\begin{cases}
p^x(1-p)^{1-x} &\text{pro $x=0,1$}\\
0 &\text{jinak}
\end{cases}\tag{1.6}
\end{equation}
Distribuční funkce je tvaru:
\begin{equation}
F(x) =
\begin{cases}
0 &\text{pro x<0} \\
1-p &\text{pro $0\leq x<1$}\\
1 &\text{pro $x\geq 1$}
\end{cases}\tag{1.7}
\end{equation}
Vztahy pro střední hodnotu a rozptyl:
\begin{align}
E(X) &= p \tag{1.8}\\
D(X) &= p(1-p)\tag{1.9}
\end{align}
Alternativní rozdělení je speciálním případem binomického rozdělení, pro $n=1$, tedy $A(p)\sim Bi(1,p)$. Ve STATISTICE není přímo implementována funkce alternativního rozdělení, používáme proto funkci binomického rozdělení, kde parametr $n$ pokládáme rovný jedné.
Příklad 1.1:
Hážeme jedenkrát kostkou. Najděte pravděpodobnostní funkci náhodné veličiny $X$, která udává, jestli v daném hodu padlo číslo menší než 3.
postup
postup v programu Statistica
Obor hodnot obsahuje dva prvky:$M=\{0,1\}$. Úspěch v našem případě znamená, že padlo číslo menší než 3, a to číslo 1 nebo 2. Neúspěch značí, že padla čísla 3, 4, 5 nebo 6.
Tedy:
$P(X=0)=\frac{4}{6}=\frac{2}{3}$
$P(X=1)=\frac{2}{6}=\frac{1}{3}$
Pravděpodobnostní funkce náhodné veličiny $X$ je tvaru:
\begin{equation}
p(x) =
\begin{cases}
\frac{1}{3} &\text{pro $x=1$}\\
\frac{2}{3} &\text{pro $x=0$} \\
\end{cases}\tag{1.10}
\end{equation}
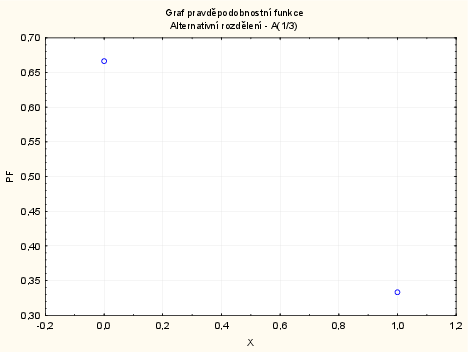
Vykreslení grafu pravděpodobnostní funkce náhodné veličiny $X\sim A(1/3)$ v systému STATISTICA:
Vytvoříme nový datový soubor o 2 proměnných a 2 případech. První proměnnou nazveme X a uložíme do ní hodnoty 0 a 1. Druhou proměnnou nazveme PF a uložíme do ní hodnoty pravděpodobnostní funkce: do dlouhého jména napíšeme: $=Binom(x;1/3;1)$.
Vykreslení grafu: Grafy - Bodové grafy - Proměnné X a PF - OK - Odškrtneme Typ proložení: lineární - OK.
Vykreslení grafu distribuční funkce náhodné veličiny $X\sim A(1/3)$ v systému STATISTICA:
Vytvoříme nový datový soubor o 2 proměnných a 4 případech. První proměnnou nazveme X a uložíme do ní hodnoty -1 až 2: do dlouhého jména napíšeme: $=v0-2$. Druhou proměnnou nazveme DF a uložíme do ní hodnoty distribuční funkce: do dlouhémo jména napíšeme: $=IBinom(x;1/3;1)$.
Vykreslení grafu: Grafy - Bodové grafy - Proměnné X a DF - OK - odškrtneme Typ preložení: lineární - OK - 2krát klikneme na pozadí grafu - Spojnice - Obecné - odškrtneme Značky -zaškrtneme Spojnice - Typ čáry: Schod - OK.
Aby náš graf lépe odrážel realitu, opět dvojklikem na pozadí grafu vybereme: Osa - Měřítko - Mód: Ručně - Minimum = -1, Maximum = 2 - OK.
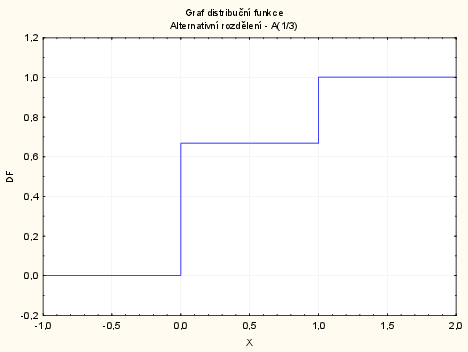
Graf distribuční funkce má schodovitý tvar, ale vertikální spojnice by se v grafu neměly vyskytovat.



