Vícerozměrné normální rozdělení: $N_n(\boldsymbol{\mu}, \boldsymbol{\Sigma})$
Uvažujme náhodný vektor $\boldsymbol{X} = (X_1, \dots , X_n)'$, reálný vektor $\boldsymbol{\mu} = (\mu_1, \dots, \mu_n)'$ a symetrickou, reálnou, pozitivně definitní matici $\boldsymbol{\Sigma} = (\sigma_{ij})_{ij=1}^n$.
Vektor $\boldsymbol{X}$ má n-rozměrné normální rozdělení s parametry $\boldsymbol{\mu}$ a $\boldsymbol{\Sigma}$, jestliže jeho hustota pravděpodobnosti má tvar:
\begin{equation}
f(x) = \frac{1}{{(2\pi)}^{\frac{n}{2}}|\boldsymbol{\Sigma}|^{\frac{1}{2}}}e^{-\frac{1}{2}(x-\boldsymbol{\mu})'\boldsymbol{\Sigma}^{-1}(x-\boldsymbol{\mu})} \qquad \text{pro $x \in \boldsymbol{R}^n$}\tag{1.9}
\end{equation}
Vztahy pro střední hodnotu a rozptyl: pro každé $i \in \{1,\dots,n\}$ platí:
\begin{align}
E(X_i) &= \mu_i\tag{1.10} \\
D(X_i) &= \sigma_{ii} = \sigma_i^2\tag{1.11}
\end{align}
Pro každé $i \in \{1,\dots,n\}$ a $j \in \{1,\dots,n\}$ platí:
\begin{equation}
C(X_i,X_j) = \sigma_{ij}\tag{1.12}
\end{equation}
Pro $n=2$ označme $\sigma_{11}=\sigma_1^2$, $\sigma_{22}=\sigma_2^2$, $\sigma_{12}=\sigma_{21}=\rho\sigma_1\sigma_2$, kde $\rho$ je koeficient korelace mezi veličinami $X_1$ a $X_2$. Pro $\sigma_1^2>0$, $\sigma_2^2>0$ a $\rho^2 \neq 1$ je hustota $f(x_1,x_2)$ tvaru:
\begin{equation}
f(x_1,x_2) = \frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}e^{-\frac{1}{2(1-\rho^2)}\Bigl[\frac{(x_1-\mu_1)^2}{\sigma_1^2}-2\rho\frac{(x_1-\mu_1)(x_2-\mu_2)}{\sigma_1\sigma_2}+\frac{(x_2-\mu_2)^2}{\sigma_2^2}\Bigr]} \\ \text{pro $x_1,x_2 \in \boldsymbol{R}^n$}\tag{1.13}
\end{equation}
Příklad 1.4:
Kurzy dvou akcí jsou náhodné veličiny, $X_1 \sim N(600,40^2)$, $X_2 \sim N(800,30^2)$. Korelace $R(X_1,X_2)=-0,4$. Jaká je pravděpodobnost, že index $X_1+X_2$ neklesne pod 1300 bodů?
postup
postup v programu Statistica
Hladáme následující pravděpodobnost: $P(X_1+X_2 \geq 1300)=$ ?
Určíme rozložení náhodného vektoru $\boldsymbol{X}=\binom{X_1}{X_2}$: kovariance je rovná: $C(X_1,X_2) = -0,4 \cdot 40 \cdot 30=-480$, tedy:
\begin{equation*}
\binom{X_1}{X_2} \sim N_2\biggl(\binom{600}{800};\begin{pmatrix} 1\,600 & -480 \\ -480 & 900
\end{pmatrix}\biggr)
\end{equation*}
Zavedeme náhodnou veličinu $Z=X_1+X_2$, která má normální rozdělení s parametry:
$E(Z) = E(X_1+X_2) = E(X_1) + E(X_2) = 600+800=1\,400$
$D(Z) = D(X_1+X_2) = D(X_1) + D(X_2) + 2C(X_1,X_2) = \\ = 1\,600 + 900 - 2 \cdot 480 = 1\,540$
Tedy: $Z \sim N(1\,400,1\,540)$ a námi hledaná pravděpodobnost je:
$P(X_1+X_2\geq 1\,300) = P(Z \geq 1\,300) = 1 - P(Z \leq 1\,300) = \\ = 1 - P(U \leq \frac{1\,300-1\,400}{\sqrt{1\,540}}) = 1 - \Phi(-2,55) = \Phi(2,55) = 0,99461$
Pravděpodobnost, že index $X_1+X_2$ neklesne pod hodnotu 1300 bodů, je 99,46 %.
Software STATISTICA využijeme jenom pro výpočet výsledné pravděpodobnosti pomocí funkce $INormal$ jednorozměrného normálního rozdělení. Vytvoříme si nový datový soubor o 1 proměnné a 1 případu, do dlouhého jména proměnné napíšeme:
$=1-INormal(1\,300,1\,400,Sqrt(1\,540))$ a dostaneme hledanou pravděpodobnost 0,99458654.
postup v programu Statistica
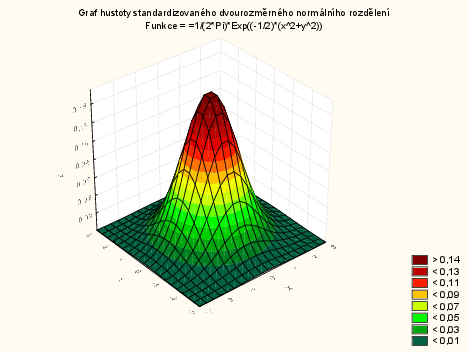
Vykreslení hustoty dvourozměrného normálního rozdělení:
Standardizované dvourozměrné normální rozdělení:
V menu vybereme: Grafy - 3D XYZ - Grafy vlastních funkcí - nastavíme rozsahy os: osa X: -3;3, osa Y: -3;3 - do pole Funkce Z(x,y) napíšeme: $=1/(2*Pi)*Exp((-1/2)*(x\hat{} 2+y\hat{} 2))$ - vybereme Možnosti 1 - odškrtneme Nadpis: Zobrazit výchozí název - do kolonky Vl.nadpis napíšeme: Graf hustoty standardizovaného dvourozměrného normálního rozdělení - potvrdíme.
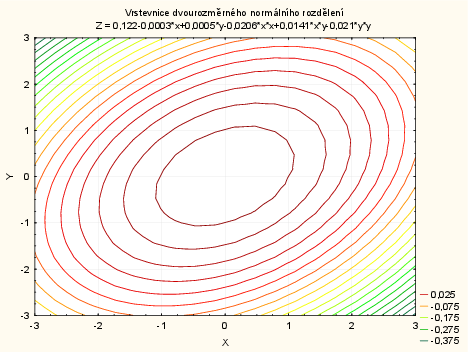
Dvourozměrné normální rozdělení, $\rho=0,75$:
V menu vybereme: Grafy - 3D XYZ - Grafy vlastních funkcí - nastavíme rozsahy os: osa X: -3;3, osa Y: -3;3 - do pole Funkce Z(x,y) napíšeme: $=1/(2*Pi*Sqrt(1-0,75\hat{}2))*Exp((-1/(2*(1-0,75\hat{}2)))*\\(x\hat{}2-2*0,75*x*y+y\hat{}2))$
- vybereme Možnosti 1 - odškrtneme Nadpis: Zobrazit výchozí název - do kolonky Vl.nadpis napíšeme: Graf hustoty dvourozměrného normálního rozdělení - potvrdíme.

Vykreslení vrstevnic dvourozměrného normálního rozdělení:
Vytvoříme nový datový soubor o 4 proměnných a 100 případech. První proměnnou nazveme X, druhou Y a do obou uložíme hodnoty v intervalu -3,3, do jich dlouhého jména napíšeme: $=Rnd(-3)+Rnd(3)$. Třetí proměnnou nazveme Z1 a do dlouhého jména napíšeme: $=1/(2*Pi)*Exp((-1/2)*(x\hat{} 2+y\hat{} 2))$. Čtvrtou proměnnou nazveme Z2 a do její dlouhého jména napíšeme: $=1/(2*Pi*Sqrt(1-0,75\hat{}2))*Exp((-1/(2*(1-0,75\hat{}2)))*\\(x\hat{}2-2*0,75*x*y+y\hat{}2))$
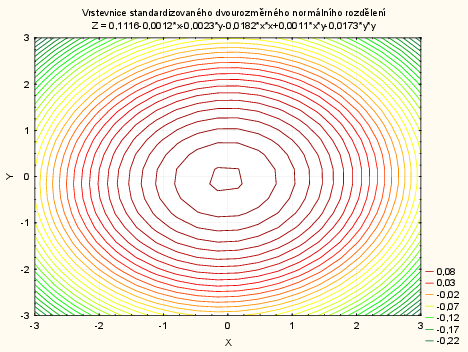
Standardizované dvourozměrné normální rozdělení:
V menu vybereme: Grafy - 3D XYZ - Vrstevnicové grafy - vybereme proměnné X,Y a Z1 - potvrdíme - zaškrtneme Proložení: Kvadratické - vybereme Možnosti 1 - odškrtneme Nadpis: Zobrazit výchozí název - do kolonky Vl.nadpis napíšeme: Vrstevnice standardizovaného dvourozměrného normálního rozdělení - potvrdíme.
Dvourozměrné normální rozdělení, $\rho=0,75$:
V menu vybereme: Grafy - 3D XYZ - Vrstevnicové grafy - vybereme proměnné X,Y a Z2 - potvrdíme - zaškrtneme Proložení: Kvadratické - vybereme Možnosti 1 - odškrtneme Nadpis: Zobrazit výchozí název - do kolonky Vl.nadpis napíšeme: Vrstevnice dvourozměrného normálního rozdělení - potvrdíme.