Rovnoměrné spojité rozdělení: $Rs(a,b)$
Náhodná veličina $X \sim Rs(a,b)$ má na intervalu $(a,b)$ konstantní hustotu pravděpodobnosti a všude jinde nulovou, tedy každá hodnota z intervalu $(a,b)$ je stejně praděpodobná.
Hustota pravděpodobnosti je tvaru:
\begin{equation}
f(x) =
\begin{cases}
\frac{1}{b-a} &\text{pro $x \in (a,b)$} \\
0 &\text{jinak}\tag{1.1}
\end{cases}
\end{equation}
Distribuční funkce je tvaru:
\begin{equation}
F(x) =
\begin{cases}
0 &\text{pro $x\leq a$} \\
\frac{x-a}{b-a} &\text{pro $x \in (a,b)$} \\
1 &\text{pro $x \geq b$}\tag{1.2}
\end{cases}
\end{equation}
Vztahy pro střední hodnotu a rozptyl:
\begin{align}
E(X) &= \frac{a+b}{2}\tag{1.3} \\
D(X) &= \frac{(b-a)^2}{12}\tag{1.4}
\end{align}
Software STATISTICA dokáže pracovat pouze s rozdělením $Rs(0,1)$, které je speciálním případem beta rozdělení s parametry 1,1. Náhodnou veličinu $X \sim Rs(a,b)$ musíme tedy transformovat na náhodnou veličinu s danými parametry, $Y \sim Rs(0,1)$, a to pomocí vztahu: $Y = \frac{X-a}{b-a}$.
Příklad 1.1:
Na prezentaci nově založené firmy je každých 20 minut promítána krátká prezentace o jejich vymezených cílech. Určete pravděpodobnost, že jestli náhodně přijdeme do promítací místnosti:
- nebudeme čekat více jak 5 minut,
- budeme čekat více jak 10 minut,
- budeme čekat 5-10 minut.
postup
postup v programu Statistica
Náhodná veličina $X$ udává dobu čekání na prezentaci, $X \sim Rs(0,20)$.
- $P(X \leq 5) = F(5) = \frac{5}{20} = 0,25$
- $P(X > 10) = 1-P(X \leq 10) = 1-F(10) = 1-\frac{10}{20} = 0,5$
- $P(5 < X \leq 10) = F(10)-F(5) = 0,5-0,25=0,25$
Řešení pomocí transformované náhodné veličiny $X$ na náhodnou veličinu $Y$: $Y=\frac{X-0}{20-0} = \frac{X}{20}$, kde $Y \sim Rs(0,1)$ a $F(y) = y$:
- $P(X \leq 5) = P(Y \leq 0,25) = F(0,25) = 0,25$
- $P(X > 10) = 1-P(X \leq 10) = 1-P(Y \leq 0,5) = 1-F(0,5) = 0,5$
- $P(5 < X \leq 10) = P(0,25 < Y \leq 0,5) = 0,5-0,25=0,25$
Řešení je možné spočítat jenom pro transformovanou náhodnou veličinu Y:
1. způsob: vytvoříme nový datový soubor o 3 proměnných a 1 případu, do dlouhého jména proměnných postupně píšeme:
- $=IBeta(0,25,1,1)$ a dostaneme výsledek 0,25
- $=1-IBeta(0,5;1;1)$ a dostaneme výsledek 0,5
- $=IBeta(0,5;1;1)-IBeta(0,25;1;1)$ a dostaneme výsledek 0,25
2. způsob: výpočet pomocí pravděpodobnostního kalkulátoru: v menu vybereme: Statistiky - Kalkulátor - rozdělení: Beta:
- $tvar 1$ - napíšeme 1, $tvar 2$ - napíšeme 1, $Beta$ - napíšeme 0,25 - Výpočet - v okénku $p$ se objeví námi hledaná pravděpodobnost: 0,25.
- $tvar 1$ - napíšeme 1, $tvar 2$ - napíšeme 1, $Beta$ - napíšeme 0,5 - (1-kumul.p) - v okénku $p$ se objeví námi hledaná pravděpodobnost: 0,5.
- pravděpodobnostní kalkulátor nám spočítá dvě hodnoty pravděpodobnosti, které potřebujeme odečíst.
$Tvar 1$ - napíšeme 1, $tvar 2$ - napíšeme 1, $Beta$ - napíšeme 0,5 - Výpočet - v okénku $p$ se objeví námi hledaná pravděpodobnost: 0,5.
$Tvar 1$ - napíšeme 1, $tvar 2$ - napíšeme 1, $Beta$ - napíšeme 0,25 - Výpočet - v okénku $p$ se objeví pravděpodobnost 0,25, tedy námi hledaná pravděpodobnost je 0,5-0,25=0,25.
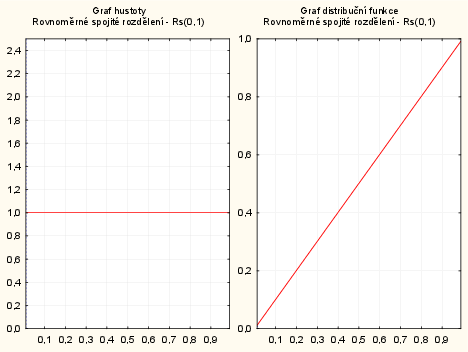
Vykreslení grafu pravděpodobnostní a distribuční funkce v systému STATISTICA pomocí pravděpodobnostního kalkulátoru:
V menu vybereme: Statistiky - Kalkulátor - rozdělení: Beta: tvar 1 - napíšeme 1, tvar 2 - napíšeme 1, p - napíšeme 0,01 - zaškrtneme Vytv.graf - Výpočet.
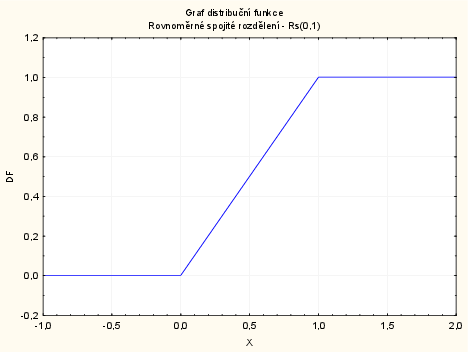
Graf distribuční funkce je možné vykreslit i nasledujícím způsobem: vytvoříme nový datový soubor o 2 proměnných a 4 případech. První proměnnou nazveme X a uložíme do ní hodnoty -1 až 2: do dlouhého jména proměnné napíšeme: $=v0-2$. Druhou proměnnou nazveme DF a uložíme do ní hodnoty distribuční funkce, do dlouhého jména této proměnné napíšeme: $=IBeta(x;1;1)$.
Vykreslení grafu: Grafy - Bodové grafy - Proměnné X a DF - OK - Odškrtneme Typ proložení: lineární - OK - 2krát klikneme na pozadí grafu - Spojnice: Obecné - odškrtneme Značky - zaškrtneme Spojnice - vybereme Osa: Měřítko - Mód: Ručně - Minimum = -1, Maximum = 2 - OK.