Binomické rozdělení: $Bi(n,p)$
V posloupnosti $n$ vzájemně nezávislých pokusů pozorujeme počet nastoupení sledovaného jevu, který v každém pokusu nastává s pravděpodobností $p$. Náhodná veličina $X$ udávající, kolikrát námi sledovaný jev nastal, má binomické rozdělení pravděpodobnosti s parametry $n$ a $p$, kde $p\in (0,1)$, píšeme: $X\sim Bi(n,p)$.
Pravděpodobnostní funkce je tvaru:
\begin{equation}
p(x) =
\begin{cases}
\binom{n}{x}p^x(1-p)^{n-x} &\text{pro $x=0,1, \dots ,n$}\\
0 &\text{jinak}
\end{cases}\tag{1.11}
\end{equation}
Distribuční funkce je tvaru:
\[F(x) = \sum_{x_i \leq x} P(X = x_i)\]
Vztahy pro střední hodnotu a rozptyl:
\begin{align}
E(X) &= np \tag{1.12}\\
D(X) &= np(1-p)\tag{1.13}
\end{align}
STATISTICA používá pro výpočet pravděpodobnostní funkce funkci $Binom(x;p;n)$ a pro výpočet distribuční funkce funkci $IBinom(x;p;n)$, kde:
$x$ = počet úspěchů,
$p$ = pravděpodobnost úspěchu v jednom pokusu,
$n$ = celkový počet pokusů.
Příklad 1.2:
Zásilka obsahuje 85 % kvalitních a 15 % nekvalitních výrobků. Náhodně s vracením vybereme 4 výrobky. Určete pravděpodobnost, že právě 3 z nich budou kvalitní.
postup
postup v programu Statistica
Náhodná veličina $X$ udává počet vybraných kvalitních výrobků , $X \sim Bi(4;0,85)$.
$P(X=3) = \binom{4}{3}0,85^{3}(1-0,85) = 0,368475$
Pravděpodobnost, že právě 3 výrobky z námi vybraných 4 budou kvalitní, je 36,85 %.
1. způsob: vytvoříme nový datový soubor o 1 proměnné a 1 případu, do dlouhého jména proměnné napíšeme:
$=Binom(3;0,85;4)$ a dostaneme výsledek 0,368475.
2. způsob: výpočet pomocí pravděpodobnostního kalkulátoru: v menu vybereme: Statistiky - Kalkulátor - Rozdělení: Binomické - N - napíšeme 4, P - napíšeme 0,85, X - napíšeme 3 - Pravděp., v okénku p se objeví vypočtená pravděpodobnost: 0,368475
Příklad 1.3:
Student má potíže se vstáváním. Pravděpodobnost, že zaspí, je 0,3. V semestru je 12 přednášek. Určete pravděpodobnost, že student:
- nestihne přednášku v polovině a více případů,
- zaspí nejvýše 2krát,
- zaspí právě 2krát,
- zaspí 2-5krát.
postup
postup v programu Statistica
Náhodná veličina $X$ udáva počet případů, kdy student zaspí, $X \sim Bi(12;0,3)$.
- $P(X\geq 6) = 1-P(X \leq 5) = 1-F(5) = \\ =1-[P(X=0) + \dotsb + P(X=5)]=1-0,882149 = 0,11785$
S pravděpodobností 11,79 % student nestihne přednášku aspoň v šesti případech.
- $P(X\leq 2) = F(2) = P(X=0)+P(X=1)+P(X=2) = 0,25281376$
S pravděpodobností 25,28 % student v průběhu semestru zaspí nejvýše 2krát.
- $P(X=2) = 0,16779$
S pravděpodobností 16,78 % student v průběhu semestru zaspí právě 2krát.
- $P(2\leq X \leq 5) = P(1\lt X \leq 5) = F(5) - F(1) = 0,8822 - 0,0850 = \\ = 0,7971$
S pravděpodobností 79,71 % student v průběhu semestru zaspí 2-5krát.
1. způsob: vytvoříme nový datový soubor se 4 proměnnými a 1 případem, do dlouhého jména proměnných postupně píšeme:
- $=1-IBinom(5;0,3;12)$ a dostaneme výsledek 0,11785874.
- $=IBinom(2;0,3;12)$ a dostaneme výsledek 0,2528.
- $=Binom(2;0,3;12)$ a dostaneme výsledek 0,1677903.
- $=IBinom(5;0,3;12) - IBinom(1;0.3;12)$ a dostaneme výsledek 0,79712621.
2. způsob: výpočet pomocí pravděpodobnostního kalkulátoru: v menu vybereme: Statistiky - Kalkulátor - Rozdělení: Binomické.
- $N$ - napíšeme 12, $P$ - napíšeme 0,3, $X$ - napíšeme 5 - Kum. pravděpodobnost, v okénku $p$ se objeví vypočtená pravděpodobnost: 0,882151, kterou však musíme ještě odečíst od jedničky, tedy námi hledaná pravděpodobnost je: 1-0,882151 = 0,117849.
- $N$ - napíšeme 12, $P$ - napíšeme 0,3, $X$ - napíšeme 2 - Kum. pravděpodobnost, v okénku $p$ se objeví vypočtená pravděpodobnost: 0,252815.
- $N$ - napíšeme 12, $P$ - napíšeme 0,3, $X$ - napíšeme 2 - Pravděp., v okénku $p$ se objeví vypočtená pravděpodobnost: 0,167790.
- Potřebujeme spočítat dvě hodnoty pravděpodobnosti:
$N$ - napíšeme 12, $P$ - napíšeme 0,3, $X$ - napíšeme 5 - Kum. pravděpodobnost, v okénku $p$ se objeví vypočtená pravděpodobnost:0,882151
$N$ - napíšeme 12, $P$ - napíšeme 0,3, $X$ - napíšeme 1 - Kum. pravděpodobnost, v okénku $p$ se objeví vypočtená pravděpodobnost: 0,085025
Výsledná pravděpodobnost: 0,882151 - 0,085025 = 0,797126.
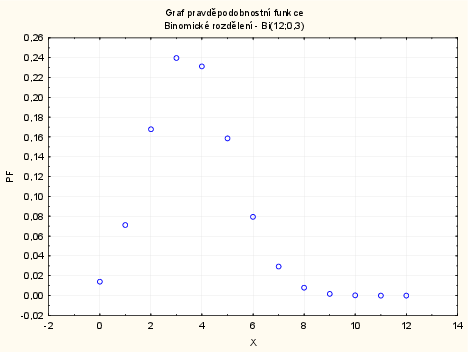
Vykreslení grafu pravděpodobnostní a distribuční funkce náhodné veličiny $X\sim Bi(12;0,3)$ v systému STATISTICA:
1. způsob: vytvoříme nový datový soubor o 3 proměnných a 13 případech. První proměnnou nazveme X a uložíme do ní hodnoty 0 až 12: do dlouhého jména proměnné napíšeme: $=v0-1$. Druhou proměnnou nazveme PF a uložíme do ní hodnoty pravděpodobnostní funkce, do dlouhého jména napíšeme: $=Binom(x;0,3;12)$. Třetí proměnnou nazveme DF a uložíme do ní hodnoty distribuční funkce, do dlouhého jména této proměnné napíšeme: $=IBinom(x;0,3;12)$.
Pravděpodobnostní funkce: Grafy - Bodové grafy - Proměnné X a PF - OK - odškrtneme Typ proložení: lineární - OK.
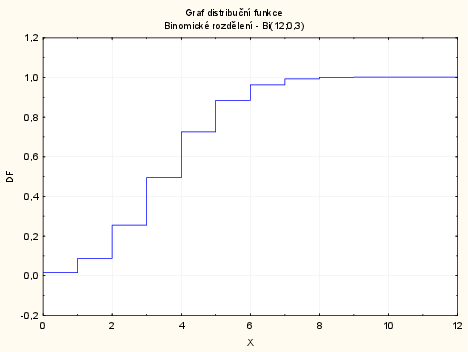
Distribuční funkce: Grafy - Bodové grafy - Proměnné X a DF - OK - odškrtneme Typ proložení: lineární - OK
- 2krát klikneme na pozadí grafu - Spojnice - Obecné - odškrtneme Značky -zaškrtneme Spojnice - Typ čáry: Schod - OK. Opět dvojklikem na pozadí grafu vybereme: Osa - Měřítko - Mód: Ručně - Minimum = 0, Maximum = 12 - OK.
2. způsob: pomocí pravděpodobnostního kalkulátoru. V menu: Statistiky - Kalkulátory - Rozdělení: Binomické. N - napíšeme 12, P - napíšeme 0,3, X - napíšeme 0 - zaškrtneme Vytv. graf - Výpočet.
Graf funkcí není z formálního hlediska správný a to v důsledku už zmiňovaných spojnic, v tomto případu též při grafu pravděpodobnostní funkce.
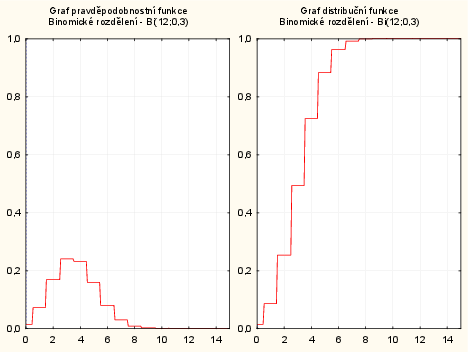
Graf distribuční funkce má schodovitý tvar, ale vertikální spojnice by se v grafu neměly vyskytovat.




