Normální rozdělení(Gaussovo): $N(\mu, \sigma^2)$
Jedná se o nejdůležitější rozdělení spojitého typu hrající zásadní úlohu v teorii pravděpodobnosti a v matematické statistice. Hustota pravděpodobnosti náhodné veličiny $X \sim N(\mu, \sigma^2)$ je symetrická podle bodu $x=\mu$ a její tvar závisí na parametru $\sigma$.
Hustota pravděpodobnosti je tvaru:
\begin{equation}
\varphi(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}} \qquad \text{pro $x \in (-\infty,\infty)$}\tag{1.5}
\end{equation}
Vztahy pro střední hodnotu a rozptyl:
\begin{align}
E(X) &= \mu\tag{1.6} \\
D(X) &= \sigma^2\tag{1.7}
\end{align}
Pomocí lineární transformace $U=\frac{X-\mu}{\sigma}$ náhodné veličiny $X$ s normálním rozdělením $N(\mu, \sigma^2)$ dostaneme náhodnou veličinu $U$ s normálním rozdělením s parametry $\mu=0$, $\sigma^2=1$. Toto rozdělení nazýváme standardizované (normované) normální rozdělení a zapisujeme: $U \sim N(0,1)$. Hodnoty jeho distribuční funkce $\Phi(u)$ jsou tabelované, též jsou tabelované jeho kvantily. Ze symetrie $\varphi(u)$ podle bodu $u=0$ vyplývají nasledující vztahy:
\begin{equation}
\begin{aligned}
\varphi(-u) &=\varphi(u) \\
\Phi(-u) &=1-\Phi(u) \qquad \text{pro $-\infty \lt u \lt \infty$}\tag{1.8}
\end{aligned}
\end{equation}
Software STATISTICA používá pro výpočet hustoty funkci
$Normal(x;mu;sigma)$, pro výpočet distribuční funkce funkci
$INormal(x;mu;sigma)$ a pro výpočet kvantilů normálního rozdělení funkci $VNormal(x;mu;sigma)$, kde:
$mu$ = střední hodnota $\mu$,
$sigma$ = směrodatná odchylka $\sqrt{\sigma^2}$.
Příklad 1.2:
Jistá firma se rozhodla podrobit své zaměstnance IQ testu. Průměrná hodnota IQ testu byla 115, směrodatná odchylka 16. Předpokládejme, že hodnoty IQ testu se řídí normálním rozdělením. Určete pravděpodobnost, že hodnota IQ testu při náhodně vybraném zaměstnanci nabude hodnoty:
- menší nebo rovné než 120,
- větší než 105,
- v rozpětí 100 až 130.
postup
postup v programu Statistica
Náhodná veličina $X$ udává hodnotu IQ testu, $X \sim N(115, 16^2)$.
- $P(X \leq 120) = P(U \leq \frac{120-115}{16}) = \Phi(0,3125) = 0,62172$
Hodnota IQ testu nabude hodnoty menší nebo rovné jak 120 s pravděpodobností 61,17 %.
- $P(X \gt 105) = 1 - P(X \leq 105) = 1- \Phi(-0,625) = \\ = 1-(1-\Phi(0,625)) = \Phi(0,625) = 0,73565$
Hodnota IQ u zaměstnance bude s pravděpodobností 73,57 % větší než 105.
- $P(100 \lt X \lt 130) = \Phi(0,9375) - \Phi(-0,9375) = \\ = 2\Phi(0,9375)-1 = 0,65278$
S pravděpodobností 65,28 % nabude IQ zaměstnance hodnoty v rozpětí 100 a 130.
1. způsob: vytvoříme nový datový soubor o 3 proměnných a 1 případu, do dlouhého jména proměnných postupně píšeme:
- $=INormal(120;115;16)$ a dostaneme výsledek 0,62266972
- $=1-INormal(105;115;16)$ a dostaneme výsledek 0,73401447
- $=INormal(130;115;16) - INormal(100;115;16)$ a dostaneme výsledek 0,65149858
2. způsob: výpočet pomocí pravděpodobnostního kalkulátoru: v menu vybereme: Statistiky - Kalkulátor - Rozdělení: Z(normální).
- průměr - napíšeme 115, $SmOdch$ - napíšeme 16, $X$ - napíšeme 120 - Výpočet - v okénku $p$ se objeví námi hledaná pravděpodobnost: 0,62267.
- průměr - napíšeme 115, $SmOdch$ - napíšeme 16, $X$ - napíšeme 105, zaškrtneme (1-kumul.p), v okénku $p$ se objeví vypočtená pravděpodobnost: 0,734014.
- Potřebujeme spočítat rozdíl dvou hodnot pravděpodobnosti:
průměr - napíšeme 115, $SmOdch$ - napíšeme 16, $X$ - napíšeme 130, zaškrtneme (1-kumul.p), v okénku $p$ se objeví vypočtená pravděpodobnost: 0,174251.
průměr - napíšeme 115, $SmOdch$ - napíšeme 16, $X$ - napíšeme 100, zaškrtneme (1-kumul.p), v okénku $p$ se objeví vypočtená pravděpodobnost: 0,825749, tedy námi hledaná pravděpodobnost je: 0,825749-0,174251 = 0,651498.
Příklad 1.3:
Nechť náhodná veličina $X \sim N(2,5)$. Určete:
- dolní kvartil,
- horní kvartil.
postup v programu Statistica
1. způsob: vytvoříme nový datový soubor o 2 proměnných a 1 případu, do dlouhého jména proměnných postupně píšeme:
- $=VNormal(0,25;2;Sqrt(5))$ a dostaneme výsledek 0,49179507
- $=VNormal(0,75;2;Sqrt(5))$ a dostaneme výsledek 3,50820493
2. způsob: výpočet pomocí pravděpodobnostního kalkulátoru:
- průměr - napíšeme 2, $SmOdch$ - napíšeme 2,236, $p$ - napíšeme 0,25, v okénku $X$ se objeví vypočtený kvantil 0,491841.
- průměr - napíšeme 2, $SmOdch$ - napíšeme 2,236, $p$ - napíšeme 0,75, v okénku $X$ se objeví vypočtený kvantil 3,508159.
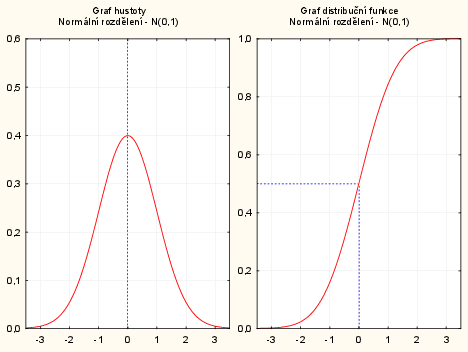
Vykreslení grafu standardizovaného normálního rozdělení pomocí pravděpodobnostního kalkulátoru:
v menu vybereme: Statistiky - Kalkulátor - Rozdělení: Z(normální), průměr - napíšeme 0, $SmOdch$ - napíšeme 1, $X$ - napíšeme 0, zaškrtneme Vytv. graf - Výpočet.