Poissonovo rozdělení: $Po(\lambda)$
Náhodná veličina $X \sim Po(\lambda)$ charakterizuje počet výskytů událostí, které nastanou za časovou jednotku. K událostem dochází náhodně, jednotlivě a vzájemně nezávisle. Průměrný počet událostí za časovou jednotku je roven parametru $\lambda$, $\lambda >0$.
Pravděpodobnostní funkce je tvaru:
\begin{equation}
p(x) =
\begin{cases}
\frac{\lambda^x}{x!}e^{-\lambda} &\text{pro $x=0,1,2,\dots $}\\
0 &\text{jinak}\tag{1.26}
\end{cases}
\end{equation}
Distribuční funkce je tvaru:
\[F(x) = \sum_{x_i \leq x} \frac{\lambda^{x_i}}{x_i!}e^{-\lambda}\]
Vztahy pro střední hodnotu a rozptyl:
\begin{align}
E(X) &= \lambda\tag{1.27} \\
D(X) &= \lambda\tag{1.28}
\end{align}
Poissonovo rozdělení je limitním případem rozdělení binomického, pro $n \rightarrow \infty$ a $p \rightarrow 0$ je $Bi(p,n) \approx Po(\lambda = np)$. Menší chyby než $10^{-2}$ se dopustíme pro $n \geq 30$ a $p\leq 0,1$.
Software STATISTICA používá pro výpočet pravděpodobnostní funkce funkci $Poisson(x;lambda)$ a pro výpočet distribuční funkce funkci $IPoisson(x;lambda)$, kde:
$x$ = počet výskytů událostí,
$lambda$ = průměrný počet událostí.
Příklad 1.10:
Předpokládejme, že realitní makléř jedná v průměru s 5 zákazníky za den. Jaká je pravděpodobnost, že počet zákazníků makléře za jeden den:
- bude větší než 4,
- bude právě 5.
postup
postup v programu Statistica
Náhodná veličina $X$ udává počet zákazníků makléře za den, $X \sim Po(5)$.
- $P(X>4) = 1-P(X \leq 4) = 1-F(4) = 1-\sum_{x=0}^4 \frac{5^x}{x!}e^{-5} = \\ = 1-0,44049=0,5595$
S pravděpodobností 55,95 % bude počet zákazníků makléře v průběhu jednoho dne větší než 4.
- $P(X=5) = \frac{5^5}{5!}e^{-5} = 0,175467$
S pravděpodobností 17,55 % bude mít v průběhu dne makléř právě 5 zákazníků.
1. způsob: vytvoříme nový datový soubor o 2 proměnných a 1 případu, do dlouhého jména proměnných postupně píšeme:
- $=1-IPoisson(4;5)$ a dostaneme výsledek 0,55950663.
- $=Poisson(5;5)$ a dostaneme výsledek 0,17546737.
2. způsob: výpočet pomocí pravděpodobnostního kalkulátoru: v menu vybereme: Statistiky - Kalkulátor - Rozdělení: Poisson.
- $Lambda$ - napíšeme 5, $X$ - napíšeme 4 - Kum. pravděpodobnost, v okénku $p$ se nám objeví vypočtená pravděpodobnost 0,440493, kterou však následně musíme odečíst od jedničky, námi hledaná pravděpodobnost je tedy: 1-0,440493 = 0,559507.
- $Lambda$ - napíšeme 5, $X$ - napíšeme 5 - Pravděp., v okénku $p$ se objeví vypočtená pravděpodobnost 0,175467.
Vykreslení grafu pravděpodobnostní a distribuční funkce náhodné veličiny $X \sim Po(5)$ v systému STATISTICA:
1. způsob: vytvoříme nový datový soubor o 3 proměnných a 15 případech. První proměnnou nazveme X a uložíme do ní hodnoty 0 až 14: do dlouhého jména proměnné napíšeme: $=v0-1$. Druhou proměnnou nazveme PF a uložíme do ní hodnoty pravděpodobnostní funkce, do dlouhého jména napíšeme: $=Poisson(x;5)$. Třetí proměnnou nazveme PF a uložíme do ní hodnoty distribuční funkce, do dlouhého jména této proměnné napíšeme: $=IPoisson(x;5)$.
Pravděpodobnostní funkce: Grafy - Bodové grafy - Proměnné X a PF - OK - odškrtneme Typ proložení: lineární - OK.
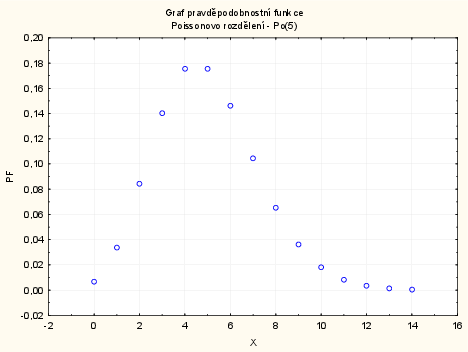
Distribuční funkce: Grafy - Bodové grafy - Proměnné X a DF - OK - odškrtneme Typ proložení: lineární - OK - 2krát klikneme na pozadí grafu - Spojnice - Obecné - odškrtneme Značky -zaškrtneme Spojnice - Typ čáry: Schod - OK. Opět dvojklikem na pozadí grafu vybereme: Osa - Měřítko - Mód: Ručně - Minimum = 0, Maximum = 14 - OK.
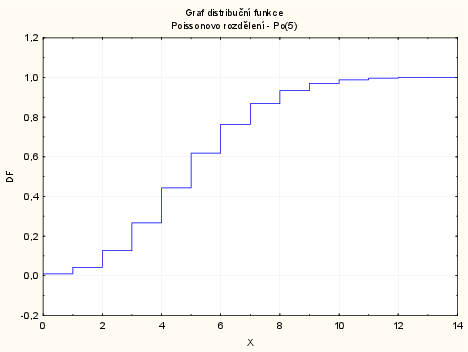
2. způsob: pomocí pravděpodobnostního kalkulátoru. V menu: Statistiky - Kalkulátory - Rozdělení: Poisson. $Lambda$ - napíšeme 5, $X$ - napíšeme 0 - zaškrtneme Vytv. graf - Výpočet.
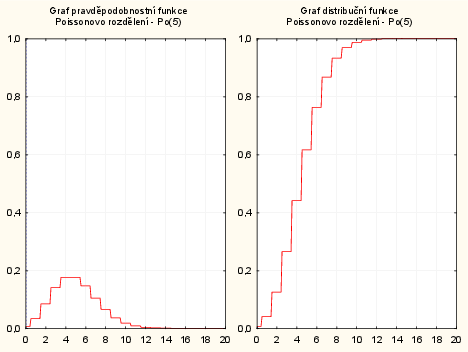
Opět není graf z formálního hlediska úplně korektní v důsledku existence svislých čar při distribuční funkci a pospojovaných hodnot pravděpodobnostní funkce.




