Studentovo rozdělení: $t(\nu)$
Náhodná veličina $X$ se řídí Studentovým rozdělením s $\nu$ stupni volnosti, píšeme $X \sim t(\nu)$, jestliže její hustota pravděpodobnosti má tvar:
\begin{equation}
f(x) =
\frac{\Gamma(\frac{\nu+1}{2})}{\Gamma(\frac{\nu}{2})\sqrt{\nu\pi}}\biggl(1+\frac{x^2}{\nu}\biggr)^{-\frac{\nu+1}{2}} \qquad\text{pro $x \in (-\infty,\infty)$}\tag{1.34}
\end{equation}
Vztahy pro střední hodnotu a rozptyl:
\begin{align}
E(X) &= 0 \qquad \text{pro $\nu\geq 2$}\tag{1.35} \\
D(X) &= \frac{\nu}{\nu-2} \qquad \text{pro $\nu\geq 3$}\tag{1.36}
\end{align}
Střední hodnota neexistuje pro $\nu=1$, pro $\nu=1,2$ neexistuje ani rozptyl. Speciálním případem Studentova rozdělení pro $\nu=1$ je Cauchyho rozdělení:
\begin{equation}
f(x) =
\frac{1}{\pi(1+x^2)} \qquad\text{pro $x \in (-\infty,\infty)$}\tag{1.37}
\end{equation}
kterého střední hodnota ani rozptyl neexistují.
Studentovo rozdělení je významné v oblasti matematické statistiky, hraje významnou úlohu při testech statistických hypotéz. Vzniká jako podíl dvou nezávislých náhodných veličin: náhodné veličiny $X \sim N(0,1)$ a náhodné veličiny $\sqrt{\frac{Y}{n}}$, kde $Y \sim \chi^2(n)$. Též se jedná o rozdělení symetrické, pro jeho kvantily platí: $t_\alpha(\nu) = -t_{1-\alpha}(\nu)$. Pro hodnoty $n>30$ ho možno aproximovat standardizovaným normálním rozdělením.
Software STATISTICA používá pro výpočet hustoty funkci $Student(x;df)$, pro výpočet distribuční funkce funkci $IStudent(x;df)$ a pro výpočet kvantilů Studentova rozdělení funkci $VStudent(x;df)$, kde:
$df$ = počet stupňů volnosti $\nu$.
Příklad 1.11:
Nechť náhodná veličina $X \sim t(9)$. Určete kvantil $t_{0,05}(9)$.
postup v programu Statistica
1. způsob: vytvoříme nový datový soubor o 1 proměnné a 1 případu, do dlouhého jména proměnné napíšeme:
$=VStudent(0,05;9)$ a dostaneme výsledek -1,8331129
2. způsob: výpočet pomocí pravděpodobnostního kalkulátoru: v menu vybereme: Statistiky - Kalkulátory - Rozdělení - vybereme rozdělení t(Studentovo), $sv$ - napíšeme 9, $p$ napíšeme 0,05, v okénku $t$ se objeví vypočtený kvantil -1,833113.
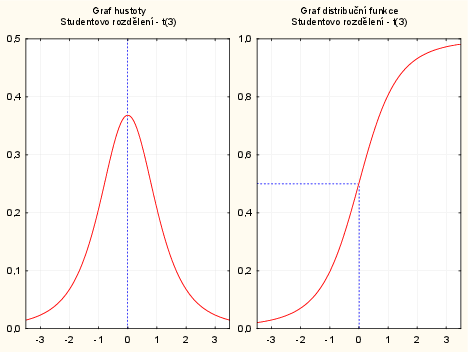
Vykreslení hustoty a distribuční funkce náhodné veličiny $X \sim t(3)$ pomocí pravděpodobnostního kalkulátoru:
v menu vybereme: Statistiky - Kalkulátory - Rozdělení - vybereme rozdělení t(Studentovo), $sv$ - napíšeme 3, $t$ napíšeme 0, zaškrtneme Vytv. graf - Výpočet.