Weibullovo rozdělení: $Wb(\delta,\varepsilon)$
Náhodná veličina $X \sim Wb(\delta,\varepsilon)$ představuje dobu čekání na nějakou událost, která se neustále může dostavit se šancí úměrnou mocninné funkci pročekané doby. Číslo $\delta>0$ se nazývá parametr měřítka a hodnota $\varepsilon>0$ se nazývá parametr formy.
Hustota pravděpodobnosti je tvaru:
\begin{equation}
f(x) =
\begin{cases}
\frac{\varepsilon}{\delta}\left(\frac{x}{\delta}\right)^{\varepsilon-1}\mathrm{e}^{-\left(\frac{x}{\delta}\right)^\varepsilon} &\text{pro $x \in (0,\infty)$} \\
0 &\text{jinak}\tag{1.23}
\end{cases}
\end{equation}
Distribuční funkce je tvaru:
\begin{equation}
F(x) =
\begin{cases}
1-\mathrm{e}^{-\left(\frac{x}{\delta}\right)^\varepsilon} &\text{pro $x \in (0,\infty)$} \\
0 &\text{inak}\tag{1.24}
\end{cases}
\end{equation}
Vztahy pro střední hodnotu a rozptyl:
\begin{align}
E(X) &= \delta\Gamma\left(\frac{1}{\varepsilon}+1\right)\tag{1.25} \\
D(X) &= \delta^2\left[\Gamma\left(\frac{2}{\varepsilon}+1\right)-\Gamma^2\left(\frac{1}{\varepsilon}+1\right)\right],\tag{1.26}
\end{align}
kde $\Gamma(x)$ je gamma funkce definovaná pro každé kladné $x$ následovně:
\begin{equation}
\Gamma(x)=\int\limits _0^\infty \mathrm{e}^{-t}t^{x-1}\, dt \tag{1.27}
\end{equation}
Pomocí Weibullova rozdělení se taktéž modeluje intenzita poruch $\lambda(x)$, která je dána vztahem:
\begin{equation}
\lambda(x) =
\begin{cases}
\frac{\varepsilon}{\delta}\left(\frac{x}{\delta}\right)^{\varepsilon-1} &\text{pro $x \in (0,\infty)$} \\
0 &\text{jinak}\tag{1.28}
\end{cases}
\end{equation}
Intenzita poruch udáva pravděpodobnost, že nastane porucha individuálního výrobku v následujícím období po okamžiku $t$ za podmínky, že do okamžiku $t$ k poruše nedošlo. Taktéž může být definována jako podíl tzv. hustoty poruch $f(t)$ a pravděpodobnosti bezporuchového provozu $R(t)$.
Weibullovým rozdělením se řídí doby životnosti mnohých zařízení, pro které nevyhovuje exponenciální rozdělení, obzvlášť ty, u kterých se projevuje mechanické opotřebení a únava materiálu. Pro volbu $\varepsilon=1$ dostaneme exponenciální rozdělení, $Ex(\frac{1}{\delta})$.
Software STATISTICA používá pro výpočet hustoty funkci $Weibull(x;b;c;theta)$, pro výpočet distribuční funkce funkci $IWeibull(x;b;c;theta)$, kde:
$b$ - parametr měřítka $\delta$,
$c$ - parametr formy $\varepsilon$,
$theta$ - parametr posunutí, který pokládáme rovný nule.
Příklad 1.9:
Předpokládejme, že doba do poruchy určité elektronické součástky je modelována Weibullovým rozdělením s kvadraticky rostoucí intenzitou poruch a s parametrem měřítka $\delta=50$.
- Jaká je intenzita poruch systému po 10-ti hodinách funkce?
- Určete pravděpodobnost, že elektronická součástka vydrží funkční více jak 60 hodin.
postup
postup v programu Statistica
Víme, že intenzita poruch je kvadraticky rostoucí funkce. Podle obecného tvaru intenzity poruch víme, že $x^{(\varepsilon-1)=2}$, tedy $\varepsilon=3$ a $X \sim Wb(50,3)$.
$\lambda(10) = \frac{3}{50}\left(\frac{10}{50}\right)^2=0,0024$
Intenzita poruch dané elektronické součástky je po 10-ti hodinách funkce 0,0024. Znamená to, že pokud byla součástka po dobu 10-ti hodin bezporuchová, pravděpodobnost, že v nasledujícím krátkém časovém intervalu $\Delta t$ dojde k její poruše, je $0,0024\Delta t$.
$P(X > 60) = 1-P(X \leq 60) = 1-F(60) = 1-[1-\mathrm{e}^{-\left(\frac{60}{50}\right)^3}] = \\ = 0,177639$
Pravděpodobnost, že elektronická součástka bude prvních 60 hodin bezporuchová, je přibližně 17,8 %.
postup bodu b.:
1. způsob: vytvoříme nový datový soubor o 1 proměnné a 1 případu, do dlouhého jména proměnné napíšeme:
$=1-IWeibull(60;50;3;0)$ a dostaneme výsledek 0,17763933
2. způsob: výpočet pomocí pravděpodobnostního kalkulátoru: v menu vybereme: Statistiky - Kalkulátory - Rozdělení - vybereme rozdělení Weibullovo, měřítko - napíšeme 50, $tvar$ - napíšeme 3, $W$ - napíšeme 60, zaškrtneme (1-kumul. p) - v okénku $p$ se objeví vypočtená pravděpodobnost 0,177639.
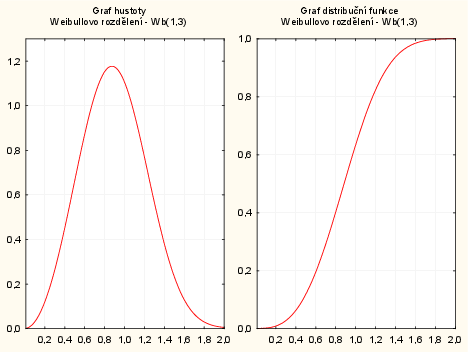
Vykreslení hustoty a distribuční funkce náhodné veličiny $X \sim Wb(1,3)$ pomocí pravděpodobnostního kalkulátoru:
v menu vybereme: Statistiky - Kalkulátory - Rozdělení - vybereme rozdělení Weibullovo, měřítko - napíšeme 1, $tvar$ napíšeme 3, $W$ napíšeme 0, zaškrtneme Vytv. graf - Výpočet.