17.7 Souřadnicové systémy

ggplot2 podporuje řadu souřadnicových systémů. Základní volbou je lineární coord_cartesian(), ale podporovány jsou i nelineární souřadnicové systémy, které se ovšem používají pouze ve velmi specifických případech jako je například vykreslování map (coord_map()). Dalším příkladem nelineárního systému je coord_polar().

Základní volbou aplikovanou v téměř všech voláních ggplot2 je bezpochyby lineární systém, ve kterém je pozice prvků určena jejich souřadnicemi na ose x a y. Základní funkcí je coord_cartesian(), ale ggplot2 obsahuje i její různé mutace a transformace:

• coord_fixed() udržuje konstantní zadaný poměr stran.
• coord_equal() je zkratka pro coord_fixed() s poměrem stran 1.
• coord_flip() prohazuje osy x a y.
• coord_trans() umožňuje provést transformaci os.
• coord_sf() je speciální funkce pro práci s mapami.

Fungování coord_flip() je možné ilustrovat pomocí jednoduchého bodového grafu. V definici mapování je váha (carat) namapována na osu x a cena na osu y:

diamonds %>% 
    ggplot(
        aes(x = carat, y = price)
    ) +
    geom_point() -> p

Použití coord_flip() prohodí osy x a y – výsledek tedy odpovídá použití aes(y = carat, x = price):

p + coord_flip()

coord_flip() je užitečné u některých specifických geomů – například u boxplotů, která zobrazují základní charakteristiky rozdělení spojité proměnné.

coord_trans() umožňuje transformovat osy podobným způsobem jako scale_*_*() funkce. Stejně jako ostatní funkce odvozené od coord_cartesian() umožňuje nastavit interval zobrazený na osách. Podobnou možnost mají opět i scale_*_*() funkce.

Nabízí se tedy otázka, na co jsou vlastně funkce coord_*() užitečné. Pro demonstraci odpovědi nasimulujeme velmi specifickou tabulku:

cltable <- data_frame(
    x = c(
        rnorm(300, sd = 2),
        rnorm(40, sd = 0.5) + 10
        ),
    y = c(
        rnorm(300, sd = 1),
        rnorm(40, sd = 0.5) + 5
        )
)

cltable %>% 
    ggplot(
        aes(x = x, y = y)
    ) +
    geom_point() +
    geom_smooth(method = "lm", se = FALSE) -> p
    
p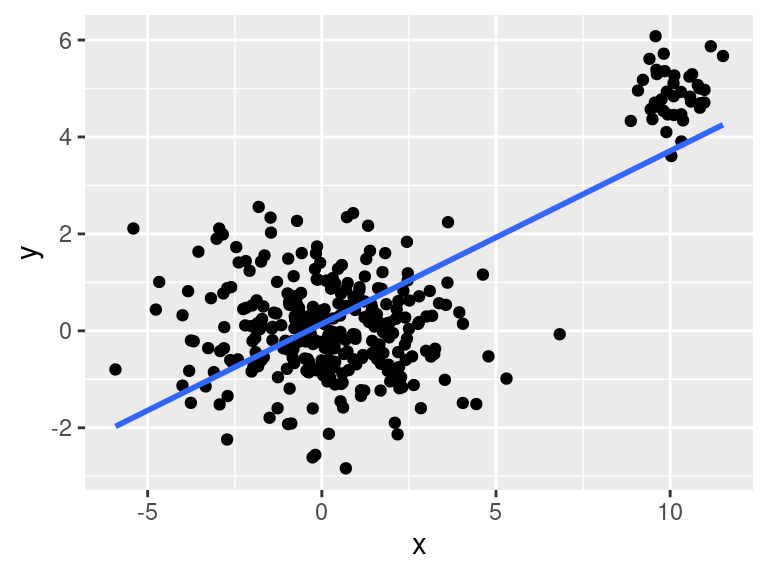

Simulovaná data obsahují dva shluky pozorování. Pokud je proložíme regresní přímkou (tj. vykreslíme statistickou transformaci dat) získáme (falešné) zdání existence rostoucího vztahu mezi veličinou na ose x a na ose y.

Řekněme, že z nějakých důvodů budeme chtít omezit zobrazené hodnoty na ose x na interval \([-5,5]\). To lez provést buď pomocí funkcí scale_x_*() nebo coord_*():

p + scale_x_continuous(limits = c(-5,5))

p + coord_cartesian(xlim = c(-5,5))

Rozdíl je zjevný. Při použití scale_x_*() je regresní přímka prakticky vodorovná. Naopak při použití coord_*() je stále rostoucí. Rozdíl je v tom, kdy je aplikované statistická transformace (v tomto případě vyhlazení). Při použití scale_*_*() funkce je nejprve omezen rozsah dat a následně je aplikována transformace. Výsledek tak může být zavádějící. Naproti tomu při použití coord_*() je nejprve aplikována transformace a následně je omezen rozsah zobrazených dat. Transformace tak reflektuje i ta pozorování, která nejsou zobrazená.

coord_*() tak nabízí možnost skutečně “zazoomovat” část obrázku, aniž by to ovlivnilo obrázek samotný.