Geometrická interpretace algebraických výrazů

Součet čísel

aritmeticky

součet čísel $3+4$

algebraicky

součet čísel $a+b$

geometricky

grafický součet úseček

Rozdíl čísel

aritmeticky

Rozdíl čísel $7-4$

algebraicky

Rozdíl čísel $a-b$

geometricky

grafický rozdíl úseček

Součin čísel

aritmeticky

součin čísel $3 \cdot 4$

$$ 3 \cdot 4 $$

algebraicky

součin čísel $a \cdot b$

geometricky

obsah obdélníka se stranami $a$, $b$

$$ a \cdot b $$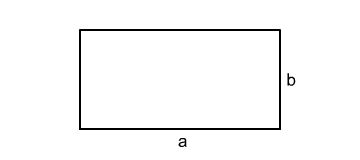

Násobení dvojčlenu jednočlenem

aritmeticky

$(20+7) \cdot 3 = 20 \cdot 3 + 7 \cdot 3 = 60 + 21 = 81$

algebraicky

$(a+b) \cdot c = ac + bc$

geometricky

$$ (a+b) \cdot c=ac+bc $$

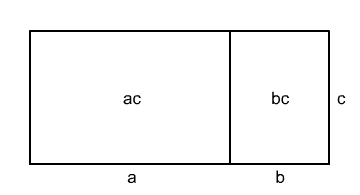
Násobení dvojčlenu dvojčlenem

aritmeticky

$(3+4) \cdot (5+6) = 5 \cdot 3 + 5 \cdot 4 + 6 \cdot 3 + 6 \cdot 4 = 15+20+18+24 = 77$

algebraicky

$(a+b) \cdot (c+d) = ac + bc + ad + bd$

geometricky

$$(a+b) \cdot (c+d)=ac+bc+ad+bd $$

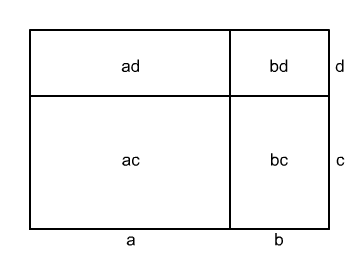
Druhá mocnina dvojčlenu $(a+b)^2$

aritmeticky

$(7+9)^2 = (7+9) \cdot (7+9) = 49+63+63+81 = 256$

algebraicky

$(a+b)^2 = (a + b) \cdot (a+b) = a^2 + ab + ab + b^2 = a^2 + 2ab + b^2$

geometricky

Narýsujeme čtverec o straně $(a+b)$. Jeho obsah je $a^2 + ab + ab + b^2 = a^2 + 2ab + b^2$.

$$ (a+b)^2 = a^2 + 2ab + b^2 $$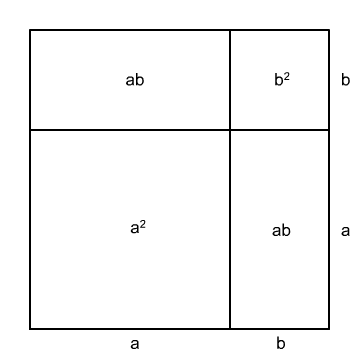

Druhá mocnina dvojčlenu $(a-b)^2$

aritmeticky

$(12-5)^2 = (12-5) \cdot (12-5) = 144-60-60+25 = 49$

algebraicky

$(a-b)^2 = (a - b) \cdot (a-b) = a^2 - ab - ab + b^2 = a^2 - 2ab + b^2$

geometricky

Narýsujeme čtverec o straně $a$, odečteme $b$.

$$ \begin{aligned} (a-b)^2 & = a^2-ab-(a-b) \cdot b \\ & = a^2-ab-ab+b^2 \\ & = a^2-2ab+b^2 \end{aligned} $$

---

$$ \begin{aligned} a^2-ab-[b(a-b)] & = a^2-ab-ab+b^2 \\ & = a^2-2ab+b^2 \end{aligned} $$

Rozdíl čtverců $a^2-b^2$

aritmeticky

$7^2-4^2 = (7-4)(7+4) = 3 \cdot 11 = 33$

algebraicky

$a^2-b^2 = (a + b) \cdot (a-b) $

geometricky