Pedagogická fakulta Masarykovy univerzity
RNDr. Růžena Blažková, CSc.
Pythagorova věta
Je dán pravoúhlý trojúhelník ABC s odvěsnami a, b a přeponou c.
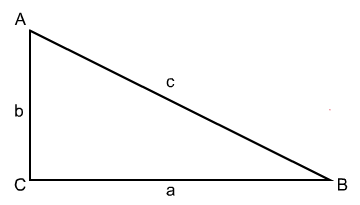
Dokažte, že v tomto trojúhelníku platí:
$$ a^2+b^2 = c^2 $$Důkaz
- geometricky
-
Sestrojíme dva čtverce o straně $a+b$ a různě je rozdělíme:
Obsahy obou čtverců se sobě rovnají:
$$ a^2 + b^2 = c^2 $$$$ (a+b)^2 = a^2 + b^2 + 4 \frac {a \cdot b} 2 $$ $$ (a+b)^2 = c^2 + 4 \cdot \frac {a \cdot b} 2 = c^2 + 2ab $$
Jiný důkaz Pythagorovy věty
- geometricky
-
Je dán pravoúhlý trojúhelník s odvěsnami $a$, $b$, přeponou $c$.
Sestrojíme čtverec o straně $a+b$.
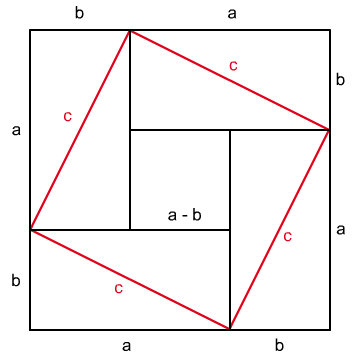
Vyjádříme obsah čtverce dvěma způsoby:
$$ \begin{array} {rlcrl} S &= 4ab + (a-b)^2 & \qquad &S&= c^2 + 4\frac {ab} 2 \\ &= 4ab + a^2 -2ab + b^2 & &&= c^2 + 2ab \\ &= a^2 + b^2 + 2ab \end{array} $$
$$ a^2 + b^2 = c^2 $$
Jiný důkaz Pythagorovy věty (James Garfield)
- geometricky
-
Je dán pravoúhlý trojúhelník s odvěsnami $a$, $b$, přeponou $c$.
Sestrojíme lichoběžník – podle animace a vypočítáme dvěma způsoby jeho obsah.
$$\frac {a^2 + 2ab + b^2} 2 = \frac {2ab + c^2 } 2$$ $$ a^2 + b^2 = c^2 $$Obsah lichoběžníka je roven polovičnímu součinu součtu obou základen a výšky. Obsah lichoběžníka je součet obsahů tří trojúhelníků. $$S=\frac {(a+b)\cdot(a+b)} 2 = \frac {a^2 + 2ab + b^2} 2 $$ $$ S = 2\frac {a \cdot b} 2 + \frac {c^2} 2 = \frac {2a\cdot b + c^2 } 2$$
Pythagorejské trojice
Pythagorejské trojice jsou trojice přirozených čísel $a, b, c$, pro které platí:
$$ a^2 + b^2 = c^2$$např. $ 3^2 + 4^2 = 5^2$
Jsou to např. čísla tvaru:
$$ \begin{aligned} a &= 2n+1 \\ b &= 2n^2 + 2n \\ c &= 2n^2 + 2n + 1 \end{aligned} $$nebo tvaru
$$ \begin{aligned} a &= 2n \\ b &= n^2-1 \\ c &= n^2 + 1 \end{aligned} $$kde $n$ je přirozené číslo.
Katedra matematiky, Pedagogická fakulta Masarykovy univerzity |
Návrat na úvodní stránku webu, přístupnost |
| Servisní středisko pro e-learning na MU
| Fakulta informatiky Masarykovy univerzity, 2015
Technické řešení této výukové pomůcky je spolufinancováno Evropským sociálním fondem a státním rozpočtem České republiky.

