Rozvoj matematických pojmů a představ u dětí předškolního věku
Pedagogická fakulta Masarykovy univerzity
RNDr. Růžena Blažková, CSc.

Vytváření matematických představ a pojmů

Pojem čísla

Při zkoumání, jakým způsobem se vytváří pojem čísla u dětí, je dobré poučit se z historie, jakým způsobem se vytvářel pojem přirozeného čísla v historickém vývoji člověka a jakým způsobem je tento pojem budován v matematice jako vědecké disciplíně, neboť obojí je východiskem chápání vývoje číselných představ u dětí od nejranějšího věku.

Pojem přirozeného čísla se v historickém vývoji vytvářel složitě, mnoho roků a člověk musel učinit velký pokrok v rozvoji svých myšlenkových procesů, aby byl schopen chápat kvantitu, tj. aby abstrahoval od viditelných vlastností předmětů a byl schopen pochopit, kolik jich je. Člověk vnímal skupiny předmětů, které ho obklopovaly, a nejprve přiřazováním poznával, zda je předmětů stejně nebo je některých více či méně (např. za každou ovci ve stádě položil kamének, nebo předmětům přiřazoval zářez na dřevěné holi, nebo kosti). Počet byl tedy nejprve vyjadřován přiřazováním, tj. vytvářením ekvivalentních množin stejných předmětů, např. prstů na rukou, kaménků, dřívek, zářezů apod. Další složitý vývoj přinesl schopnost zapsat tuto skutečnost a vyjádřit ji slovem a postupně se tak vyvíjely číslice, číslovky a číselné soustavy.

V matematice se pojem přirozeného čísla buduje buď pomocí čísel kardinálních nebo čísel ordinálních nebo pomocí Peanovy množiny. Při velmi stručném přiblížení můžeme uvést:

Pojem čísla kardinálního se opírá o pojem tříd navzájem ekvivalentních množin a přirozená čísla zaváděná pomocí čísel kardinálních dávají vesměs odpověď na otázku „kolik to je“. Pojem čísla ordinálního se opírá o uspořádané množiny a podobná zobrazení mezi uspořádanými množinami a přirozená čísla pomocí nich zaváděná dávají většinou odpověď na otázku „kolikátý“. Přirozená čísla budovaná pomocí Peanovy množiny vycházejí z prvního prvku a pomocí tohoto prvku a pojmu následovníka se vybuduje množina všech přirozených čísel. Teoretické základy budování pojmu přirozeného čísla jsou uvedeny v publikacích aritmetiky a algebry a didaktické přístupy k zavádění přirozených čísel v publikacích didaktiky matematiky.

Postupné vytváření pojmu čísla

Všímejme si, jak dvouleté až tříleté dítě vnímá počet věcí kolem sebe. Nejprve ukazuje: tam jsou dvě, tam také jsou dvě, později tři. Když mu ukážeme hromádku prvků o větším počtu než tři, odmítá říct, kolik to je a zpravidla řekne: “to je moc”. Postupně však vnímá další čísla, až v šesti letech je schopno určit počet prvků ve skupinách, ve kterých je jich šest až deset. Při vnímání počtu předmětů musí dítě učinit obrovský pokrok ve svém myšlení, a to tak, že postupně přestává vnímat viditelné vlastnosti předmětů, jako je barva, tvar, materiál, ze kterého jsou zhotoveny, zda jsou živé či neživé a všímá si pouze toho, kolik jich je. To znamená, že začne vnímat, že mezi určitými skupinami objektů existuje něco společného, co nesouvisí s jejich viditelnými vlastnostmi, ale s tím, že mají prvky, které se dají vzájemně jednoznačně přiřadit, tj. že jich je stejně. Přitom se však nejde o žádnou cílenou výuku matematiky, ale všechny nové poznatky dítě získává prostřednictvím her a běžných činností souvisejících s jeho životem. Současně se rozvíjí jeho komunikace verbální (zdokonaluje se jeho řeč) i nonverbální (využívá např. své značky v mateřské škole, kreseb, symbolů). Postupně se zkvalitňuje jeho vnímání, paměť, představivost i pozornost, což je nezbytné pro jeho další matematický rozvoj. Děti jsou přirozeně tvořivé a jejich tvořivosti je třeba účelně využít a dávat jim takové podněty, které přispívají k rozvoji jejich myšlení.

Číslo, podobně jako jiné abstraktní pojmy, nemůžeme vnímat smysly, vnímáme pouze reprezentanty těchto čísel. Například reprezentantem čísla čtyři mohou být čtyři auta, čtyři děti, čtyři jablíčka apod. Ale také např. bydlíme ve čtvrtém poschodí, náš dům má číslo 4, jsou čtyři hodiny, mám 4 roky apod. Děti se seznamují s kvantitativní stránkou jevů v kontaktu s okolním světem, pomocí konkrétních předmětů se postupně propracovávají k obecnějšímu chápání až k pochopení abstraktního pojmu čísla. Mnohokrát opakovaná činnost s konkrétními předměty vede k získávání zkušeností dětí, že nezáleží na tom, s jakými předměty pracují, ale pouze na tom, že je jich stejně. Musí se také naučit číslo pojmenovat a zapsat. K tomu, aby proces vytváření čísla byl pro děti snadný, využíváme mnoho činností, ve velké většině nematematických. Např. při skládání kostek domina, hraní hry Člověče, nezlob se apod. Přitom však se nemůže nic uspěchat, protože k pojmu čísla se každé dítě dopracuje samostatně vlastní činností, až mu tzv. „svitne“. Připomeňme, že prvotně dítě vnímá kvantitu vzájemně jednoznačným přiřazováním předmětů a teprve až ho někdo naučí počítat, tak počítá předměty po jedné. Tedy pojem čísla si dítě vytvoří samo svou vlastní myšlenkovou činností a řadu čísel 1, 2, 3 atd. jej někdo naučí.

Co všechno může dítě vnímat na konkrétních předmětech? Dejme do neprůhledného sáčku např. 4 koláče a nechme děti povídat, co všechno o nich mohou říct. Sledujme, jaké mají představy – zrakové, chuťové, čichové, hmatové, čím jsou koláče naplněny, kam je mohou přemístit (např. na talíř). Kolik z dětí je však již ve „světě matematiky“ a zeptá se “kolik jich je”?

V první fázi se děti naučí chápat čísla 1 až 5, později až do deseti a nulu. Měly by umět vytvořit skupinu o daném počtu prvků, zapsat počet prvků dané skupiny, čísla porovnávat. Než se však dospěje k pojmu přirozeného čísla, je třeba dávat dětem mnoho podnětů, které souvisí s jejich hrami a činnostmi, které běžně každý den provádějí a které s matematikou zdánlivě nesouvisí. Pokud se tato fáze podcení, dochází u některých dětí problémům při vytvoření pojmu čísla.

Poznámka: Někdy se děti již v předškolním věku seznamují s číslem nula. S nulou je třeba zacházet jako s jakýmkoliv jiným číslem a není vhodné spojovat ji se slovem „nic“. Nulu je třeba chápat jako počet prvků prázdné množiny (počet jablíček na prázdném talíři) nebo jako číslo, které získáme odčítáním sobě rovných čísel (měl jsem 3 švestky, všechny jsem snědl). Pokud číslo 0 nerespektujeme jako číslo rovnocenné ostatním, děti je v budoucnu podceňují i ve významu čísla, i ve významu v zápisu čísla (např. 304 chápou jako 34).

Cvičení k vytvoření pojmu čísla vyplývající z běžných činností a her

S dětmi provádíme elementární cvičení, která jsou propedeutikou k pozdějšímu chápání pojmu čísla. Nejprve se jedná se o běžné činnosti s hračkami, obrázky a dalšími předměty, využívají se pohádky, hry apod., přičemž se vyčleňují některé charakteristické vlastnosti se zapojením více smyslů.

Práce s předměty

Dětem předkládáme různé předměty, které je obklopují, a snažíme se o to, aby uvedly názvy nebo jména předmětů – co to je, jak se to jmenuje. Zároveň zkoumají viditelné vlastnosti předmětů – jaké jsou, zda jsou živé, neživé, jaká je jejich barva, jaký je jejich tvar, z jakého jsou materiálu. Nejprve pracujeme s izolovanými předměty, později s dvojicemi, trojicemi předmětů a skupinami více předmětů.

Identifikace předmětů, osob, zvířat apod.

Děti mohou identifikovat předměty, osoby, zvířata pohledem, hmatem, chutí, čichem apod., tedy svými smysly.

Charakteristika předmětů

Děti provádějí charakteristiku předmětů z různých hledisek, např. z čeho to je, jaké to je, k čemu to je, co dělá, kdo to je, kdo něco dělá apod.

Diferenciace

Jedná se o hledání shod a rozdílů mezi předměty – je to stejné jako …, je to jiné než …, čím se liší – např.:

který předmět (obrázek) nepatří mezi ostatní:

který předmět (obrázek) má jinou barvu než ostatní:

který předmět (obrázek) má jiný tvar než ostatní:

který předmět (obrázek) má jinou velikost než ostatní:

který předmět (obrázek) má jinou polohu než ostatní:

Vyhodnocení situací

Jde o pohled zpět, utvrzení správnosti a rozhodnutí: Je to tak?, Je to správně?

Komparace (srovnání)

Porovnávání předmětů probíhá z mnoha hledisek. Předměty jsou stejné, podobné, nejsou stejné, jsou různé. V čem se liší, v čem jsou stejné (např. v pohádce Dlouhý, Široký a Bystrozraký – porovnáváme výšku, tloušťku apod.)

Nejprve porovnáváme objekty, které dítě vidí současně, později s tím, co je uchováno v paměti (jak to bylo před tím, je to tak, jak to bylo původně, jak to má být, co se změnilo)

Pro matematiku je to důležitá činnost – např. při psaní číslic porovnává dítě to, co napíše, s předlohou, se vzorem na začátku linky v sešitě.

Dále se porovnávají předměty v různých polohách – vedle sebe, pod sebou, jinak umístěné.

Porovnává se množství – vztahy více, méně, stejně – příprava na porovnávání čísel.

Zpřesňování

Jde o zpřesňování původní, vstupní informace, většinou s využitím smyslového vnímání. Využíváme otázek typu: Kdo je to?, Co je to? Dalšími poskytnutými informacemi přibližujeme přesný význam – např. hra na řemesla, které zvíře myslím, apod. Zde se uplatňuje orientace na sluch (ptáme se slovy) nebo na zrak (předvádíme pantomimu), nebo a hmat (hmatem se určuje předmět). Může se také určovat kvantita nebo vzájemné postavení objektů.

Negace

Spočívá na využití předpony “ne” – např. je to živé – neživé, létá to, nelétá to, je to modré, není to modré. Přitom dbáme na jasné vyjádření, kdy předmět danou vlastnost má či nemá (např. negace vyjádření „je to bílé“ není „je to černé“).

Závislosti

Využíváme pravidelného opakování skupin prvků, rytmizace – vytváření dvojic, trojic prvků, které se pravidelně opakují (navlékání korálků různých barev, stavby hradeb z krychlí apod.).

Gradace

Jde o určení polohy a pořadí prvků v realitě i na obrázku – je to blíž než, dál než, vlevo od, vpravo od, nad, pod, za.

Činnosti směřující k vytvoření pojmu přirozeného čísla

Mezi činnosti, které cíleně směřují k vytváření předpokladů pro správné pochopení přirozeného čísla patří klasifikace, přiřazování, uspořádání.

Třídění (klasifikace)

V matematice souvisí třídění s rozkladem množiny. Při rozkladu množiny na podmnožiny musí být splněny požadavky:

1. Každý prvek základní množiny musí být zařazen do některé z podmnožin.
2. Žádný prvek nemůže být současně ve dvou podmnožinách.
3. Sjednocením všech podmnožin je základní množina.

Třídění se provádí podle určité charakteristické vlastnosti, děti mají za úkol roztřídit dané předměty na ty, které požadovanou charakteristickou vlastnost mají a na ty, které ji nemají. Přitom charakteristická vlastnost musí být stanovena jednoznačně (např. nestačí určit malý – velký, když se třídí více předmětů různých velikostí). Vzniknou tak dvě, později více skupin a přitom každý prvek musí být zařazen v některé ze vzniklých skupin podle daného kriteria. Nejprve se provádí třídění dichotomické (na dvě skupiny), později trichotomické (na tři skupiny), atd.

Vymezení charakteristické vlastnosti se provádí na předmětech denní potřeby, např. vybírá se co se jí, co se obléká, sportovní náčiní, pracovní nářadí, čím jezdíme apod.

Jídlo se pak dále vymezuje např. na ovoce, zeleninu, pečivo, mléčné výrobky apod., sportovní náčiní podle jednotlivých sportů atd.

Zařazování předmětů do skupin podle stejné vlastnosti, např.:

• Panenky – chodící, nechodící.
• Auta – osobní, nákladní.
• Kostky ze stavebnice, (např. 2 velikosti, 3 barvy, 4 tvary).
• Geometrické tvary (trojúhelníky, čtverce, kruhy).
• Umisťování příborů do příborníku (lžíce, vidličky, nože, malé lžičky).
• Ukládání nádobí do skříňky – hrníčky, talířky, talíře hluboké, mělké.
• Atd.

Třídění předmětů provádějí děti prakticky při každém úklidu hraček.

Přiřazování

Při přiřazování předmětů poznávají děti skupiny objektů, které mají společné to, že každému prvku v jedné skupině je přiřazen právě jeden prvek druhé skupiny a naopak (prvky jsou vzájemně jednoznačně přiřazeny). Přitom si děti postupně uvědomují, že skupiny, jejichž prvky lze vzájemně jednoznačně přiřadit, mají stejně prvků a že nezáleží na tom, jakého druhu prvky jsou. Postupně zvyšujeme náročnost na abstrakci – od konkrétních předmětů k symbolům a k číslu. Přiřazujeme tedy:

1. předměty předmětům

   Pro pochopení pojmu přirozeného čísla je vhodné využívat činností, kdy děti přiřazují předměty předmětům (zpočátku tak, aby v obou skupinách bylo předmětů stejně – vytvářejí dvojice). Umisťují např. panenky do kočárků, auta do garáží, přiřazují děvčata chlapcům, pomeranče dětem, hrníčky na podšálky, vajíčka do kalíšků, apod.

   Velmi vhodnou činností je prostírání nádobí a příborů na stůl – u stolečku sedí Jirka, Petr, Terezka, Irenka, každému přiřadíme talířek, lžičku, skleničku.

   Využíváme i pohádkových postav nebo postav z večerníčků – kdo ke komu patří:

   Hurvínek – Spejbl, Maková panenka – motýl Emanuel, Rumcajs – Manka, Mach – Šebestová, Křemílek – Vochomůrka, Jeníček – Mařenka, Zlatovláska – Jiřík, Bob – Bobek, Ája – Fík, atd.

2. symboly předmětům

   Vybereme několik dětí, jindy hraček (do pěti), přiřazujeme prsty, kamínky, tyčinky, obrázky apod.

3. symboly symbolům

   Obrázkům přiřazujeme např. puntíky, tyčinky, tyčinkám puntíky apod.

4. předmětům a symbolům čísla

   Skupinám předmětů nebo symbolů přiřadíme číslo – kolik jich je.

Např.

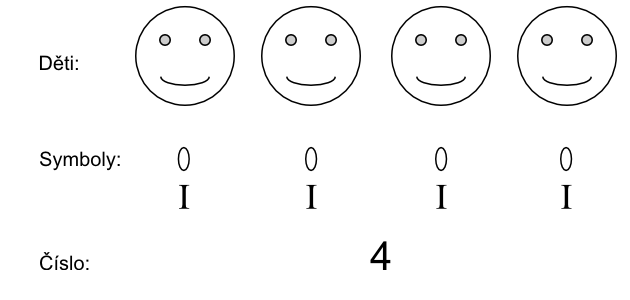
Každá správná učebnice matematiky pro první třídu obsahuje dostatek těchto činností a před tím, než uvede číslo, dostatečně dlouho procvičuje prostřednictvím obrázků přiřazování symbolů předmětům, např. na obrázku jsou zvířátka, děti kreslí tolik puntíků (čárek apod.), kolik je na obrázku zvířátek.

Uspořádání

Uspořádání děti vnímají zcela přirozeně na naprosto nematematických činnostech, při hrách, prostřednictvím pohádek, říkadel aj. Cílem činností je, aby si děti v budoucnu postupně uvědomily, že množina přirozených čísel je uspořádaná, že je možné o každých dvou prvcích rozhodnout, který je před kterým. (Toto je již učivem 1. stupně ZŠ.)

V období předčíselných představ uvádíme pohádky, ve kterých hraje roli posloupnost dějů či uspořádání osob. Jsou to například pohádka O kohoutkovi a slepičce, pohádka O veliké řepě, Zlatovláska, aj. Děti si velmi dobře pamatují posloupnost dějů v pohádkách. Přitom děti chápou uspořádání v obou směrech.

Současně se ujasňují pojmy “první prvek”, “poslední prvek” v dané skupině. Zde je třeba správného zdůvodnění, neboť se musí pracovat se všemi prvky dané skupiny a první nebo poslední prvek je třeba vymezit vzhledem k ostatním prvkům dané skupiny. Např. v pohádce O veliké řepě: Proč je dědeček první – protože všichni ostatní jsou za ním. Chybně by bylo – protože před ním nikdo není. Proč je myška poslední – protože všichni ostatní jsou před ní. Opět chybné zdůvodnění by bylo – protože za ní nikdo není.

Dalšími činnostmi mohou být např. uspořádání dětí v řadě podle velikosti, skládání pastelek podle velikosti, navlékání korálků podle určitého pravidla, kdy děti mají pravidlo dodržet, stavby z krychlí podle pravidla, apod. Děti jsou podněcovány k činnostem, např.:

• postavte panenky od nejmenší po největší podle výšky
• seřaďte auta podle délky od nejkratší po nejdelší
• postavte se do řady podle velikosti (výšky) od největšího po nejmenšího
• postavte s kostek stavebnice komíny, z kolika kostek jste postavili nejvyšší komín?