Pedagogická fakulta Masarykovy univerzity
RNDr. Růžena Blažková, CSc.
Přirozená čísla
Význam čísla
Již v předškolním věku poznávají děti číslo v mnoha jeho významech, uveďme tedy některé:
- Označení množství (počtu prvků): 5 dětí, 3 medvídci, 10 jablek, 4 prsty, apod.
- Číslo jako operátor (pokyn ke změně): přidej mi tři bonbóny, uber mi dva knedlíky, apod., o kolik mám víc, než ty, aj.
- Číslo jako adresa (pořadí, uspořádání): bydlíme v domě číslo 24, ve třetím poschodí, narodil jsem se 15.6., apod.
- Číslo jako kód – např. kódy na zabezpečovacích zařízeních, PIN, telefonní číslo.
- Číslo jako veličina (míra) – 2 kg banánů, moje výška je 130 cm, aj.
Čísla v různých významech děti zcela přirozeně používají. V každém případě by se však měly seznámit nejprve s číslem ve významu množství a teprve potom ve významu pořadí a s číselnou řadou. Je třeba si také uvědomit, že s čísly v různých významech nelze zacházet stejně, např. sčítat a odčítat můžeme čísla ve významu množství – počtu prvků, ale není to možné ve významu čísla jako adresy.
Pojem čísla ve významu počtu prvků je třeba vytvářet mnoha různými činnostmi.
- Čísla 1 a 2 spojujeme s částmi těla (Dítě a jeho tělo): Kolik máš očí, rukou, nohou, nosů, brad, apod.
- Kolik nás je doma?
- Kolik mám kamarádů nebo kamarádek?
Při vytváření čísla 3 (a dalších v oboru do pěti) umístíme na stůl tři předměty (nejprve stejného druhu, později předměty různé) a dáváme dětem úkoly:
- Řekni, kolik předmětů (jablíček, kostek, kaštanů apod.) vidíš na stole.
- Kde ještě vidíš stejně věcí jako na stole.
- Ukaž tolik prstů.
- Polož kartičku, na které je stejně puntíků jako jablíček na stole.
- Doplň, aby byly tři (když je na stole méně jablíček než 3)
- Na obrázcích jsou různé předměty v různém počtu (nejprve od 1 do 5). Vyber ty obrázky, na kterých jsou tři prvky.
Využíváme i pohybových her, např.
- na zemi nakreslíme kruhy, do každého zapíšeme některé z čísel 1 až 5 a děti se mají postavit do kruhů podle vyznačených čísel (je nutné, aby všechny děti byly zařazeny v některém z kruhů).
- umístíme dětem na záda kartičky s puntíky (od jedné do pěti) a děti se mají rozdělit do skupin tak, aby v každé skupině byly děti se stejným počtem puntíků na zádech.
- rozdáme dětem kartičky s tečkami od jedné do pěti a požadujeme, aby vytvořily vždy řady pěti dětí tak aby kartičky byly uspořádané od jedné do pěti.
(Využití zejména v oblastech Dítě a společnost, Dítě a svět.)
Dalším důležitým poznatkem je, že změnou konfigurace se počet prvků nemění. Dětem dáme pět tyčinek a vyzveme je, aby z nich něco vytvořily. Děti tak vytvářejí různé sestavy, např. sestavují domeček, šipku a nejrůznější obrázky podle vlastní fantazie a tyčinek je stále pět.
Např.
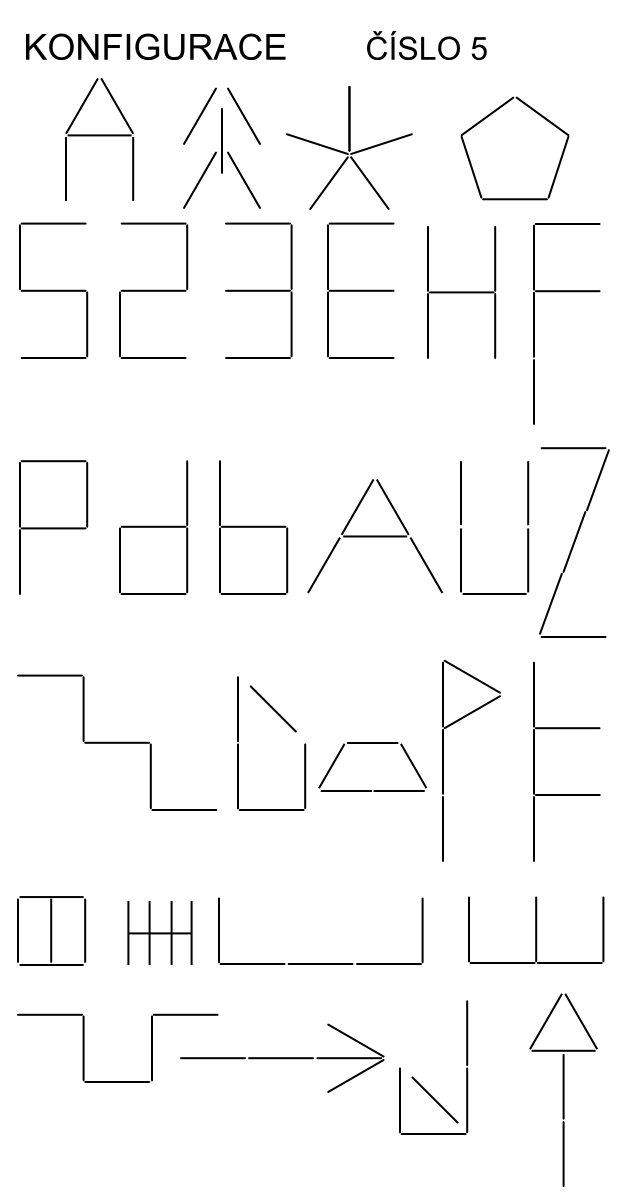
Podobně sestavují různé stavby z pěti stejných krychlí, např.:
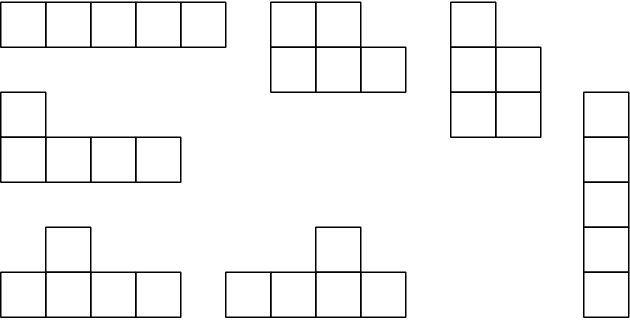
Intuitivně přicházejí k závěru, že změnou tvaru obrázku nebo stavby se nezmění počet prvků.
Využíváme pohádky, ve kterých hraje roli počet osob nebo předmětů, např. Tři zlaté vlasy děda Vševěda, Tři oříšky pro Popelku, Sněhurka a sedm trpaslíků, Pohádka o dvanácti měsíčkách, aj. Téměř na každé číslo od 1 do 12 lze vybrat nějakou pohádku.
Čísla od jedné do pěti znázorněná pomocí nějakých prvků děti zpravidla poznají bez počítání – zejména když jsou ve vhodném seskupení, jako např. na kostce pro hru Člověče, nezlob se.
Počítání po jedné
Uvědomme si, co vlastně děláme, když počítáme po jedné. Máme-li skupinu předmětů, u kterých na první pohled nepoznáme, kolik jich je, zpravidla ukazujeme na jednotlivé předměty prstem (nebo je označíme tužkou) a ke každému přiřadíme jedno slovo ze známé řady číslovek – jedna, dvě, tři, … až patnáct (např.) a poslední vyslovená číslovka udává počet prvků ve skupině. Tímto vlastně skupinu předmětů uspořádáme a každému předmětu přiřadíme prvek z uspořádané skupiny číslovek.
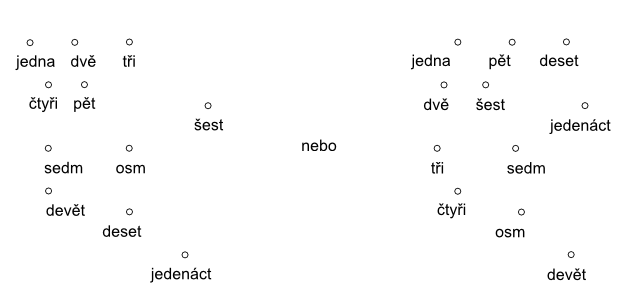
Cílem je, aby děti uměly vyjmenovat řadu čísel od jedné do pěti, později do deseti, a to vzestupně i sestupně. Přitom však za každou vyslovenou číslovkou by měly vidět počet prvků a aby nepoužívaly pojmy bezobsažně, bez významu.
Při počítání po jedné je třeba respektovat, aby:
- nebyl vynechán žádný prvek,
- žádný prvek se nepočítal dvakrát,
- při změně konfigurace předmětů nedošlo k chybnému počítání, kdy názvy čísel jsou vázány těsně na určité předměty,
- konkrétní předměty nebyly počítány od nuly.
Pokud bychom učili děti pouze vyjmenovat řadu slov (číslovek) od jedné do deseti a děti vytvořenou neměly představu čísla tak, aby si za každým slovem uměly představit počet prvků, dojde většinou k tomu, že děti např. počítají: jedna, dvě, tři, čtyři, sedm, pět, čtyři …, tj. říkají jakási slova bez obsahu.
(Číselná řada je jednou z očekávaných kompetencí dítěte v předškolním věku.)
Využíváme mnoha říkadel a básniček, kdy se postupně číselná řada opakuje:
- Jedna, dvě, Honza jde, nese pytel mouky.
- Jedna, dvě, tři, my jsme bratři.
- Jedna, dvě, tři, čtyři, pět, cos to Janku, cos to sněd.
- Jedna, dvě, Honza jde.
- Jedna, dvě, tři, pes ho větří.
- Jedna, dvě, tři, čtyři, kampak si to míří?
- Jedna, dvě, tři, čtyři, pět, běží k mámě na oběd.
Pro čísla do deseti např. Oře, oře Jan, přiletělo k němu devět vran.
Vyžíváme i hádanek (čtyři rohy, čtyři nohy …).
Vhodnou činností je dokreslování obrázků, kdy děti spojují postupně body označené čísly např. od jedné do 24.

Číslo a číslice
K zápisu čísel používáme znaky – číslice neboli cifry. V poziční desítkové soustavě používáme deset znaků (jednička, dvojka, …, devítka, nula) a pomocí těchto deseti znaků zapíšeme jakékoliv číslo. Ve vyjadřování bychom měli rozlišovat pojmy číslo a číslice již v předškolním věku, usnadníme tím dětem chápání těchto pojmů ve školním věku. Např. pětka může být menší než jednička (ve smyslu číslice – znaku): 5 1, ale číslo 5 je vždy větší než číslo 1. Pojmy jako osmička, desítka, dvacítka ve významu čísla k vyjadřování mezi dětmi nepatří. Děti se postupně naučí psát všech deset číslic, to je však učivem 1. ročníku základní školy. Psaní číslic se řídí normou.
Ke snadnějšímu pochopení tvarů číslic můžeme využívat figurek nebo polštářků ve tvaru číslic. Některé děti mají problémy s rozlišováním některých číslic tvarově podobných (např. 6, 9), děti, které mají problémy s pravolevou orientací, mají problém zapamatovat si, jak se píší např. 1, 3, 7. V současné době se děti velmi brzy učí znát i digitální zápis číslic.
V literatuře existuje mnoho publikací, které dětem číslice přibližují, např. J. Lada: Veselé obrázky, F. Halas: Počitadlo, V. Nezval: Říkadla.
Připomeňme, že v různých civilizacích se používaly různé znaky k zápisu čísel a číslice, které my používáme, měly také svůj vývoj a svůj původ mají v Indii a arabských zemích.
Desítková soustava
V historickém vývoji používal člověk různé číselné soustavy (nepoziční, poziční, o základech 2, 5, 10, 20, 60), nyní umíme počítat v číselných soustavách o jakémkoliv přirozeném základu. Ze všech číselných soustav se jako nejvýhodnější udržela poziční soustava desítková. Deset jednotek nižšího řádu tvoří vždy jednu jednotku řádu o jednu vyššího (deset jednotek tvoří jednu desítku, deset desítek tvoří jednu stovku, atd.). V poziční desítkové soustavě používáme k zápisu čísla deseti znaků (číslice 0 až 9) a pomocí nich zapíšeme jakékoliv číslo. Každá číslice v zápisu čísla má jednak hodnotu vlastní (počet jednotek příslušného řádu) a hodnotu místní (na které pozici se nachází). Např. v čísle 333 je vlastní hodnota každé číslice 3, místní hodnota záleží na umístění v zápisu čísla.
Intuitivní chápání poziční desítkové soustavy se začíná projevovat při práci s čísly od 10 do 20, kdy by děti měly postupně chápat, že např. v zápisu čísla 15 „1“ znamená 10 jednotek.
Pozůstatky šedesátkové soustavy používáme při měření času – 60 minut je jedna hodina, 60 sekund je jedna minuta. Toto je pro některé děti obtížné, avšak částečná orientace v čase je jednou z očekávaných kompetencí na konci předškolního období. U některých dětí postačí časová orientace ve smyslu dříve – později (včera, dnes, zítra, ráno, poledne, večer) a potom nenásilné seznamování s časovými údaji. Velmi vodné je využití časového snímku dne s příslušným časovým údajem.
Pedagogická Fakulta, Masarykova univerzita |
Návrat na úvodní stránku webu, přístupnost |
| Servisní středisko pro e-learning na MU
| Fakulta informatiky Masarykovy univerzity, 2010
Technické řešení této výukové pomůcky je spolufinancováno Evropským sociálním fondem a státním rozpočtem České republiky.

