Porovnávání čísel

Porovnávání přirozených čísel se v matematice opírá o pojem zobrazení, nebo se k porovnávání využívá zápisu čísla (u víceciferných čísel) nebo se používá číselná osa. V období vytváření číselných představ je vhodné využít zobrazení, avšak než se začnou přirozená čísla porovnávat, je třeba dodržet určitý vývoj.

1. Nejprve je třeba, aby děti pochopily vztahy “více”, “méně”, “stejně”.

   K tomu se používá mnoho her, konkrétních činností s předměty, kreslení obrázků a vždy se vysloví závěr, čeho je více, čeho je méně a čeho je stejně.

   Jde např. o vytváření dvojic dětí (děvče – chlapec), dvojic panenka – kočárek, auto – garáž, aj.

   Na daných souborech konkrétních předmětů nebo na obrázcích děti rozhodují kterých prvků je více nebo méně (event. stejně).

   

2. Další činnosti spočívají v tom, aby děti přidaly nebo dokreslily prvky podle pokynů: Polož na stolek stejně lžiček jako je hrníčků, přines stejně jablíček, jako je dětí, nakresli více mrkví, než je králíků, nakresli méně vajíček než je slepic apod.

3. Teprve po těchto činnostech se přiřazují skupinám prvků čísla a porovnávají se přirozená čísla. Přitom je nutné dobře vysvětlit znaky používané pro porovnávání (<, >, =), protože, ač je to málo pochopitelné, mnoha dětem činí používání těchto znaků problémy.

4. Až se zvládne porovnávání přirozených čísel, učí se děti zjistit, o kolik má jedna skupina prvků více či méně než druhá.

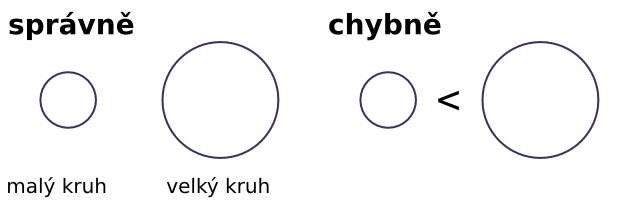
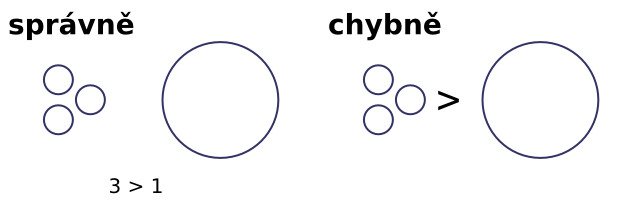
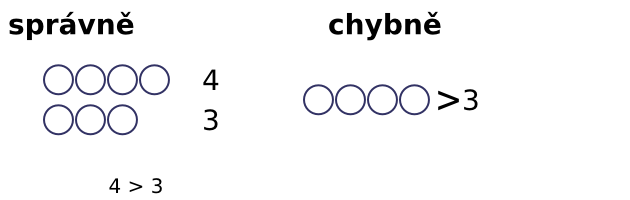
Při porovnávání přirozených čísel můžeme narazit na určitá úskalí. Prvním z nich je, aby se správně rozlišovalo mezi porovnáváním velikostí předmětů a porovnáváním jejich počtu. Děti rozlišují tvar: např. velký míč a malý míč, ale počet: je jeden velký míč a jeden malý míč. Nelze mezi předměty umisťovat znaky <, >, =. Tyto znaky lze umístit pouze mezi čísla.

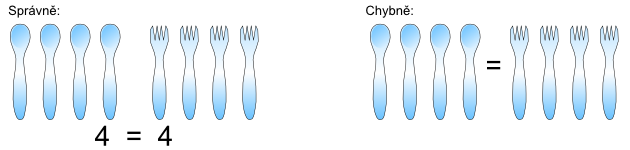
Dalším úskalím je, když se porušuje rozdíl mezi skupinami, které mají stejný počet prvků, např. 4 lžičky a 4 vidličky a skupinami, které se sobě rovnají (nepochopení rovnosti a ekvivalence množin). Dítě velmi dobře vnímá, že vidlička a lžička se nerovnají, ale že jich je stejně. Chybné obrázky, ve kterých se umístí rovnítko mezi dvě skupiny různých objektů, které mají stejně prvků, jeho správné představy deformují.

Poznámka: Znázorňování přirozených čísel na číselné ose, kdy číslu odpovídá bod na přímce, je pro děti velmi složité. Děti zpravidla chápou číslo zapsané u bodu na číselné ose, nikoliv však bod. Také znázorňování přirozených čísel úsečkou na číselné ose je nesprávné.

Některé propedeutické činnosti však můžeme realizovat – kdy dětem na části přímky znázorníme např.:

• Když mi byl 1 rok, začal/a jsem chodit.
• Když mi byly 3 roky, začal/a jsem chodit do mateřské školy,
• Až mi bude 6 roků, začnu chodit do 1. třídy.
• Kolik mi bude roků, až budu chodit do třetí třídy?