1 Pojem funkce více proměnných
2 Limita a spojitost funkce
 2.1 Metrické vlastnosti 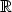ⁿ
 2.2 Limita funkce
 2.3 Spojitost funkce
 2.4 Věty o spojitých funkcích
3 Parciální derivace
 3.1 Parciální derivace 1. řádu
 3.2 Derivace vyšších řádů
 3.3 Směrové derivace
 3.4 Lagrangeova věta o střední hodnotě
4 Diferenciál funkce
 4.1 Diferencovatelná funkce, diferenciál
 4.2 Diferenciály vyšších řádů
 4.3 Kmenová funkce
5 Derivace složené funkce, Taylorův vzorec
 5.1 Parciální derivace složených funkcí
 5.2 Taylorova věta
6 Lokální a absolutní extrémy
 6.1 Lokální extrémy
 6.2 Absolutní extrémy
7 Zobrazení mezi prostory vyšších dimenzí
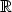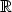 7.1 Zobrazení z ² do ²
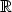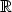 7.2 Zobrazení z ⁿ do ^m
 7.3 Diferenciální operátory matematické fyziky
8 Funkce zadaná implicitně
 8.1 Implicitně zadaná funkce jedné proměnné
 8.2 Implicitně zadaná funkce více proměnných
 8.3 Implicitně zadané zobrazení mezi prostory vyšších dimenzí
9 Vázané extrémy
 9.1 Metoda Lagrangeových multiplikátorů
 9.2 Vázané extrémy a nerovnosti
10 Generování grafiky v Maplu
 10.1 Graf funkce dvou proměnných
 10.2 Vrstevnice
11 Výpočty limit v Maplu
 11.1 Ilustrační grafika
 11.2 Výpočty
12 Derivace funkce v Maplu
 12.1 Parciální derivace 1. řádu
 12.2 Geometrický význam parciálních derivací
 12.3 Derivace vyšších řádů
 12.4 Směrové derivace
 12.5 Parciální derivace složených funkcí
13 Aproximace funkce v Maplu
 13.1 Diferencovatelná funkce
 13.2 Tečná rovina ke grafu funkce
 13.3 Užití diferenciálu k přibližným výpočtům
 13.4 Taylorova věta
 13.5 Kmenová funkce
14 Extrémy funkce v Maplu
 14.1 Lokální extrémy
 14.2 Absolutní extrémy
 14.3 Vázané extrémy
15 Funkce zadaná implicitně v Maplu
 15.1 Generování PC-grafu funkce zadané implicitně
 15.2 Výpočty
16 Software pro podporu výuky matematické analýzy
 16.1 Systémy počítačové algebry
 16.2 Public-domain programy
 16.3 Materiály na Internetu